局部多孔质气体静压径向轴承的建模与仿真

吴 笛

(西昌学院 工程技术系，四川 西昌 615013)

气体静压轴系的研究一直是超精密机床的重点研究内容之一[1]，随着气体静压导轨与主轴在超精密机床上的广泛应用，高刚度、高精度、结构简单和阻尼特性良好的静压轴承成为超精密机床设计追求的目标。近年来，多孔质类型的气体静压轴承的设计与制造成为研究的热点[2]，多孔质气体静压轴承采用具有透气性能的多孔质材料作为节流器，由多孔质材料的流体阻抗产生节流效果。与小孔节流型及狭缝节流型气体静压轴承相比，多孔质气体静压轴承结构相对简单，具有较高的承载能力、刚度和更高的阻尼，且稳定性较好[3]。为满足超精密机床的发展需要，设计出更高刚度、更高精度、更低成本的气体静压轴承已经成为目前超精密机床制造亟待解决的问题。

1 数学建模

1.1 基本量描述及初始条件

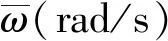
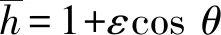
(1)

图1 局部多孔质气体静压径向轴承结构图

考虑Beavers-Joseph全速度滑移模型[4]：

(1)当y=0，rp≤(dp/2)，0≤θp≤2π时，

(2)

v=vp

(3)

(4)

式中：u，v，w为气流速度分别在x，y，z方向的速度分量；φx，φy，φz分别为多孔质材料3个坐标方向上的黏性渗透系数。

(2)当y=0，rp>(dp/2)，|z|≤(L/2)，0≤|θ|≤2π时，u=0，v=0，w=0。

(3)当y=h，|z|≤(L/2)，0≤|θ|≤2π时，

(5)

(6)

(7)

1.2 建立气膜内气体压力分布数学模型

按照局部多孔质矩形止推轴承的推导方法[5]，则可以得到稳态条件下，简化Beavers-Joseph速度滑移模型的局部多孔质气体静压径向轴承无量纲气膜压力的分布方程：

(8)

气体在多孔质内流动符合Darcy定律：

(9)

(10)

(11)

式中：up，vp，wp分别为气体在多孔质内部3个坐标方向上的速度分量，m/s；pp为气体在多孔质内任意点的压力，Pa。

由(9)～(11)式和气体连续性方程[6]，可以得到稳态条件下气体在局部多孔质节流器内部无量纲的气体压力分布方程：

(12)

建立边界条件如下：

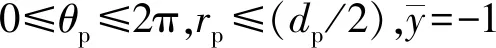
根据局部多孔质气体静压径向轴承的边界条件，采用弱积分原理[7]把(8)式和(12)式转换成相应的积分形式，然后使用有限元的方法将2个积分方程分别进行离散化处理。离散后的2个方程是相互耦合的非线性方程，需要反复迭代来进行解耦求解，直到相邻2次求解的压力分布差值小于预设的值(可根据实际情况选取小值)即可停止迭代，从而得到气体薄膜内的压力分布情况。

在迭代解耦的过程中，会遇到有限元方程的收敛性求解问题，针对这个问题可以参考文献[8],利用适用于多孔质轴承的比例分割因子，可以方便地求解出任意间隙下的气膜压力分布值，同时计算速度也比较快。

1.3 局部多孔质气体静压径向轴承特性描述

径向轴承的承载分为径向分量Wr和切向分量Wθ，分别表示如下：

(13)

(14)

承载的无量纲形式为：

(15)

(16)

(17)

轴承角为：

(18)

(19)

轴承的气体质量流量可以利用速度边界进行积分求得：

(20)

使用Beavers-Joseph全滑移模型得到局部多孔质气体静压径向轴承的气体质量流量：

(21)

气体质量流量的无量纲形式为：

(22)

式中：R为理想气体常数，J/kg·K；Ta为外部环境气体绝对温度，K；ρa为外部环境大气密度，kg/m3。

2 静态特性仿真

2.1 仿真条件

进行仿真的局部多孔质气体静压径向轴承的基本参数为：长度L=100 mm，直径D=100 mm；多孔质节流器的厚度H=5 mm，节流器直径d=5 mm，多孔质材料均匀，各向同性，渗透系数φx=φy=φz=1×10-13m2，速度滑移系数α=0.1，供气压力ps-pa=0.4 MPa，环境压力pa=0.1 MPa，仿真温度Ta=298 K，气体动力黏度η=1.8×10-5Pa·s；轴承面上的多孔质节流器个数为16个，分两排周向均布，两排的位置分别位于L/4处；轴承工作平均半径间隙为18 μm；无量纲参考间隙h0=5 μm。静态条件下，轴承工作面相对运动速度U=0 m/s。

2.2 仿真试验

2.2.1 平均半径间隙对静态特性的影响

其他参数不变，取不同的轴承平均半径间隙，研究不同的偏心率对径向轴承的静态特性影响，仿真试验结果如图2所示。从图2a可以看出，在同一偏心率条件下，当间隙由10 μm递增到18 μm的过程中，轴承承载能力随着平均半径间隙的增加而增加；但是，当间隙由18 μm递增到22 μm时，轴承承载能力却随平均半径间隙的增加而下降。在同一半径间隙条件下，轴承承载均随偏心率的增加而增加，但在偏心率较大处，承载增加的幅度变小。

从图2b可以看出，当轴承平均半径间隙增加到12 μm时，轴承的刚度达到最大值，此时的偏心率为零；随着平均半径间隙的增加，轴承的刚度呈下降趋势，并且对应的最佳刚度也逐渐偏离偏心率为零的位置，如当轴承的平均半径间隙为22 μm时，最佳刚度位于偏心率约为0.3的位置。

图2 平均半径间隙对轴承承载和刚度的影响

2.2.2 供气压力对静态特性的影响

其他参数不变，仅改变轴承的供气压力，则仿真结果如图3所示。可以看出，随着供气压力的提高，轴承的无量纲承载能力增加，并且对应的无量纲刚度也成比例增加，增加的幅度明显。说明提高供气压力可以明显改善轴承的承载和刚度。

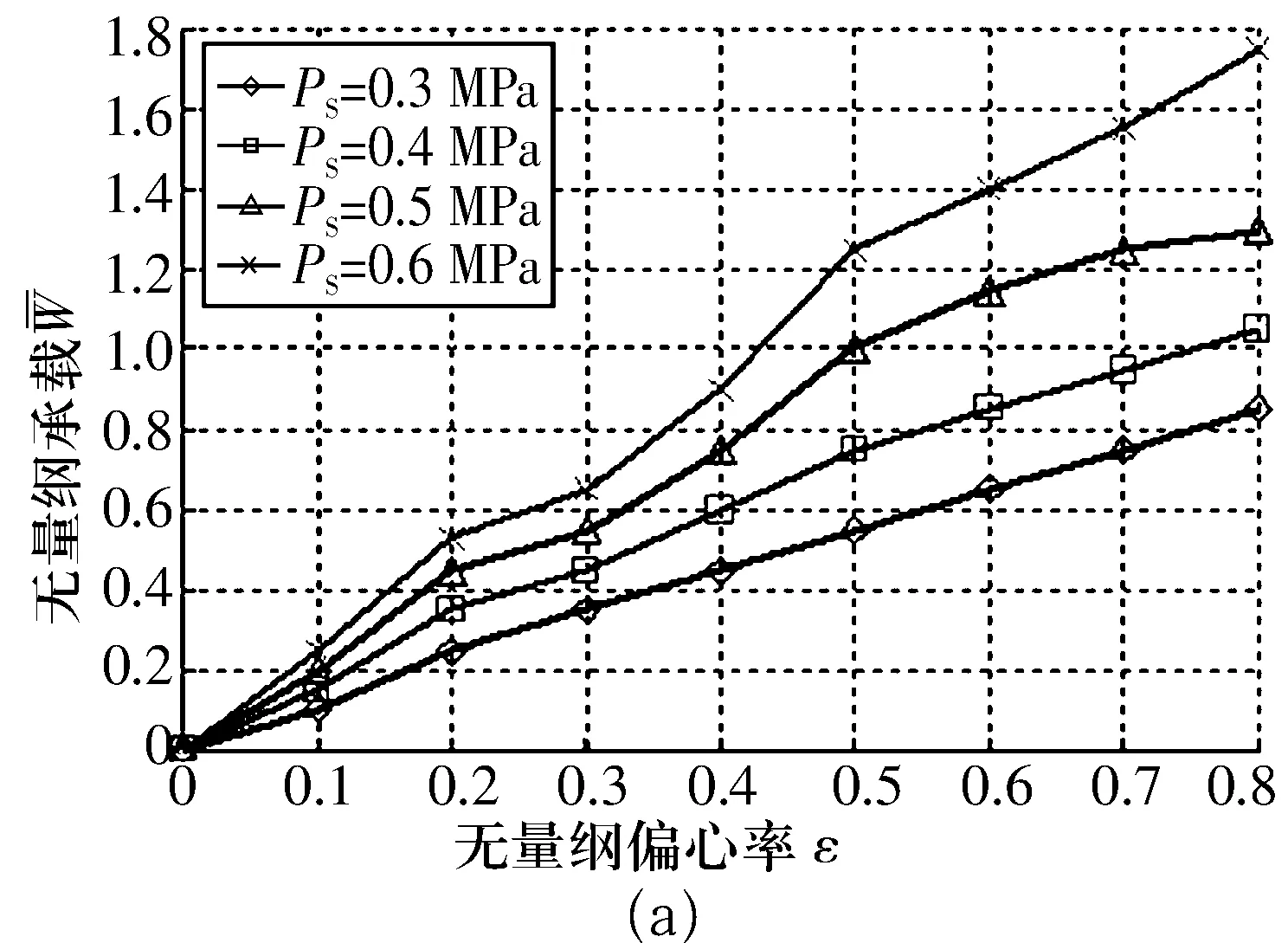
图3 供气压力对轴承承载和刚度的影响

2.2.3 节流器直径对静态特性的影响

其他参数不变，仅改变轴承的多孔质节流器直径，仿真结果如图4所示。在图4a中，随着多孔质节流器直径的增大，径向轴承的承载并不随着节流器直径的增加而增加，在不同的偏心率段，存在着最佳的节流器直径值。例如，当偏心率小于0.6时，直径为6 mm的轴承承载值最大；当偏心率大于0.6时，直径为4 mm的轴承承载值最大。在图4b中，刚度也同样遵循类似的规律，当偏心率小于0.5时，直径为6 mm的轴承刚度最大，而当偏心率大于0.5时，直径为4 mm的轴承刚度最大。

2.2.4 节流器渗透系数对轴承静态特性的影响

其他参数不变，仅改变节流器渗透参数，其仿真结果如图5所示。从图5a可以看出，径向轴承承载并不随着节流器渗透系数的降低而降低，而存在着最佳的渗透系数值，其中，当渗透系数为1×10-13时，对应的轴承承载在整个偏心率段具有最大值。从图5b可以看出，刚度也同样遵循类似的规律，当渗透系数为1×10-13时，对应的轴承刚度最大，并且最大刚度点在偏心率为零处。

图4 节流器直径对轴承承载和刚度的影响

图5 节流器渗透系数对轴承承载和刚度的影响

2.2.5 节流器厚度对轴承静态特性的影响

其他参数不变，仅改变节流器厚度，其仿真结果如图6所示。在图6a中，当偏心率小于0.2时，轴承的承载随着节流器厚度的增加而减少，但是相差不多；当偏心率在0.2和0.6之间时，承载随着节流器厚度的增加而逐渐增加，当厚度为4 mm时轴承的承载最大；当偏心率大于0.6时，厚度为8 mm时轴承的承载最大，而厚度为2 mm时轴承的承载最小。

在图6b中，在相同的偏心率下，节流器厚度为4 mm时对应的径向轴承的刚度最大，并且最大刚度位于偏心率为零处。其他厚度对应的轴承的刚度相对较小，并且最大刚度点均不在偏心率为零处，如节流器厚度为8 mm时，最大刚度点对应的偏心率在0.3处。

图6 节流器厚度对轴承承载和刚度的影响

2.2.6 节流器个数对轴承静态特性的影响

其他参数不变，仅改变节流器个数，其仿真结果如图7所示。从中可以看出，径向轴承的承载和刚度随着节流器个数的增加而增加，但是当节流器个数增加到一定数量时，承载、刚度反而呈下降趋势。当多孔质节流器个数为32时，轴承的承载和刚度最大。

2.2.7 轴承长度对静态特性的影响

其他参数不变，仅改变轴承的长度，其仿真结果如图8所示。从中可以看出，轴承的承载并不随着轴承长度的增加而增加，而是在给定的轴承直径条件下，轴承长度为80 mm时其承载和刚度最大。

2.2.8 轴承直径对静态特性的影响

其他参数不变，仅改变轴承的直径，其仿真结果如图9所示。从图9a可以看出，在同一偏心率条件下，径向轴承的承载随着轴承直径的增大而增大；在同一轴承直径条件下，轴承的承载随着偏心率的增加而增加。从图9b可以看出，在同一偏心率条件下，轴承的刚度随着轴承直径的增大而增大；在同一轴承直径条件下，轴承的刚度随着偏心率的增加而呈下降趋势。当轴承的直径大于120 mm时，轴承的承载和刚度随着直径增加而增加，但增加的效果已经不显著了。

图7 节流器个数对轴承承载和刚度的影响

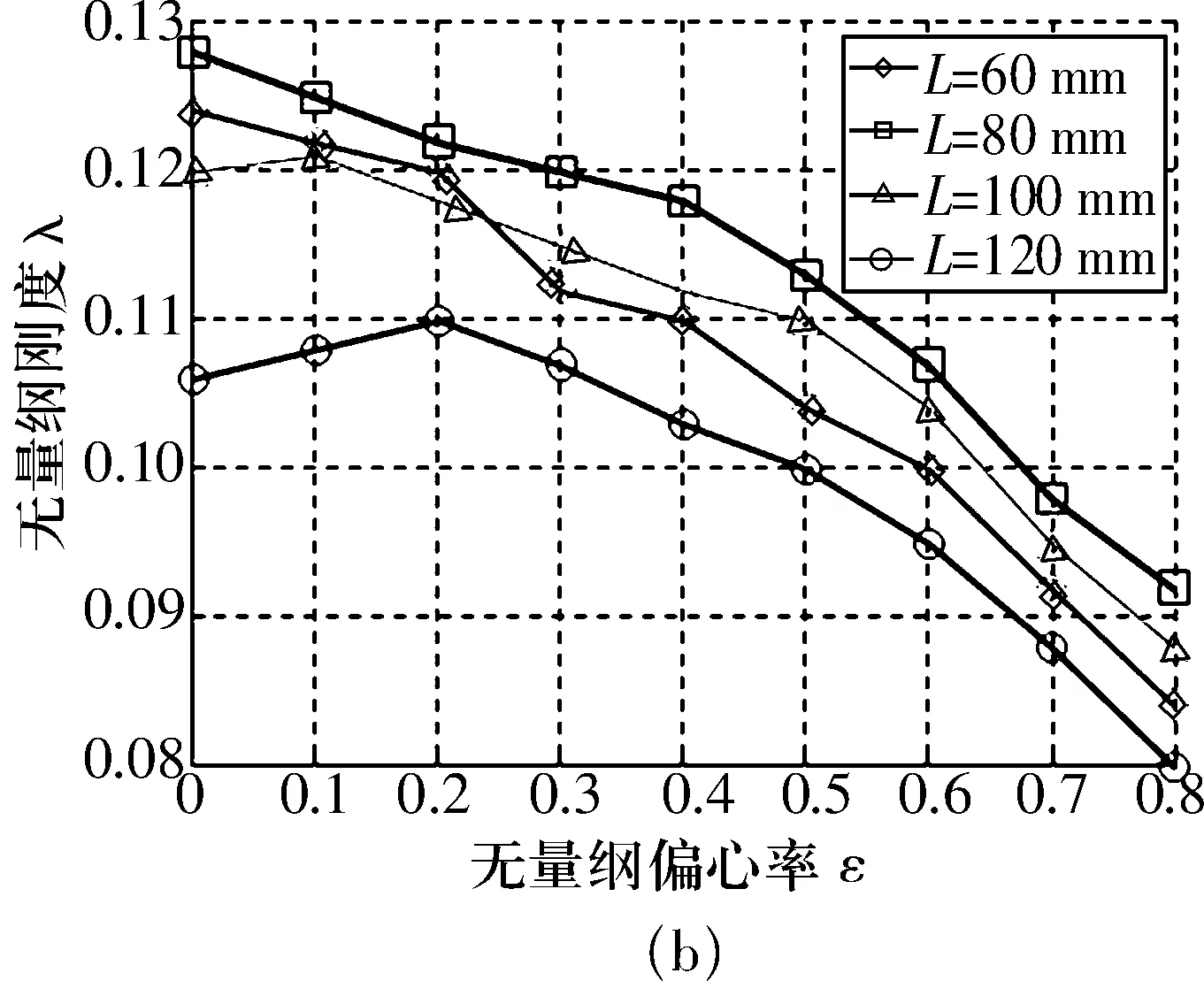
图8 轴承长度对轴承承载和刚度的影响

3 结论

根据多孔质气体静压径向轴承参数对轴承静态特性影响的仿真，得到多孔质气体静压径向轴承的设计准则如下：

图9 轴承直径对轴承承载和刚度的影响

(1)不同的轴承平均半径间隙在全偏心率范围内，对应着不同的承载、刚度特性，只有选择合适的平均半径间隙才能分别获得最大的承载值和刚度值，并且最大刚度在偏心率为零时取得；当取远离最佳平均半径间隙的工作间隙时，轴承的最大刚度值的取得就会偏离偏心率为零的位置。

(2)多孔质节流器的直径、厚度、渗透系数对径向轴承静态特性的影响存在着最佳匹配关系，只有选择合适的直径、厚度、渗透系数才能获得满意的径向轴承性能。

(3)外部供气压力对径向轴承的特性影响效果显著，适当增大供气压力可以获得较高的承载和刚度。

(4)随着轴承直径的增大，可以获得较高的承载和刚度，但是对给定长度的径向轴承来说，当轴承径长比增大到D/L=6/5后，承载和刚度增加的幅度变得很小，基本保持不变；保持轴承直径不变，改变轴承的长度，发现径长比为D/L=5/4时，轴承获得最佳的承载和刚度。

(5)节流器个数对径向轴承特性的影响存在着最佳值，只有设计合适的节流器个数才能获得满意的轴承承载和刚度。