柔性转子-轴承系统非线性动力学行为分析

郑美茹，黑 棣，贾 良，吕延军

(1.陕西铁路工程职业技术学院 机电系，陕西 渭南 714000；2.西安理工大学 机械与精密仪器工程学院，西安 710048)

轴承转子系统是一个典型的非线性动力系统,仅用线性理论已不能解释系统所表现出的某些动力行为。由于线性稳定性理论的局限性,以往仅研究了转子系统平衡点解的稳定性,而转子总是具有影响系统稳定性的质量偏心,而该影响在线性分析中无法考虑,因此必须运用非线性分析方法研究其动力学特性[1-3]。

实际的转子轴承系统严格地说来都是柔性系统，因此，开展柔性转子轴承系统稳定性的研究具有重要的工程意义[4]。Newmark方法是一种常用的动力分析数值计算方法。由于工程技术中振动分析问题的复杂性,数值分析方法成为动力反应分析的重要手段[5-6]。分析了Newmark法在计算时间步长内产生的影响计算精度和计算稳定性的计算扰动效应，并将其改进形成一种考虑了计算扰动的求解周期响应的局部迭代方法。运用Runge-Kutta法对改进的Newmark直接积分法计算结果进行了对比。

1 柔性转子系统动力学方程

图1所示为某流体动压滑动轴承支承的对称柔性转子动力系统，其动力学方程可写为：

(1)

式中：M,C和K分别为转子的质量、阻尼和刚度矩阵；f为轴承的非线性油膜力矢量；Q为施加在转子上的周期激励力(与转速同步的不平衡激励或汽动力激励)矢量；X为转子的位移矢量。分别表示为：

图1 流体动压滑动轴承-柔性转子系统示意图

2 改进的Newmark直接积分法

在时刻t+Δt的响应值应满足动力平衡方程：

(2)

由常平均加速度假设可得:

(3)

(4)

式中：a6=Δt(1-γ);a7=γΔt,其中γ≥0.5;a≥0.25(0.5+γ)2。

(5)

(6)

0.25(0.5+γ)2。

将(5)和(6)式代入(2)式可得关于Xt+Δt的方程:

(7)

第i个Δt时间段的位移增量为：

(8)

(9)

第i个时间步长的加速度增量为:

(10)

根据运动约束条件和Δt时间步长内的加速度增量，可得Δt时间步长内的速度增量为:

(11)

由(8)式、(10)式和(11)式可以进一步计算出ti+1=ti+Δt时刻系统的位移、速度和加速度:

Xi+1=Xi+ΔXi

(12)

(13)

(14)

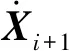
(15)

(16)

将(15)式改写为:

(17)

将(16)式代入(17)式可得:

(18)

(19)

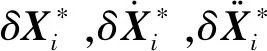
(20)

(21)

(22)

将(18)式和(19)式相加，可得:

(23)

式中：

(24)

(25)

(26)

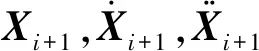
3 数值算例及结果

图轴承处的轴心轨迹

图轴承处的准周期轨迹

图轴承处的Poincaré映射点列

图 轴承处y方向的时间历程

图7 轴承处y方向的分岔图

图8 圆盘处y方向的分岔图

4 结束语

基于Newmark直接积分法，分析了在计算时间步长内产生的、影响计算精度和计算稳定性的计算扰动效应。提出了改进的Newmark直接积分法，从而减少了计算结果误差、超越现象和提高了计算稳定性。虽然不可能完全消除Newmark法直接积分的计算误差和完全保证其计算结果收敛，但能使计算位移、速度和加速度符合计算运动约束条件。应用改进的Newmark直接积分法得到的数值结果展现系统具有周期运动、准周期运动等非线性现象。改进的Newmark直接积分法具有理论和现实意义，在振动分析中有很好的应用价值。