倾覆力矩对推力球轴承疲劳寿命的影响
罗继伟,伍海云
(1.洛阳轴研科技股份有限公司,河南 洛阳 491039;2.奥新(厦门)轴承有限公司,福建 厦门 361021)
1 前言
在滚动轴承标准中,推力球轴承基本额定寿命的计算公式为[1]:

式中:Ca为额定动载荷;Pa为与实际载荷等效的当量载荷。标准规定的计算公式为:

式中:Fr和Fa分别是作用于轴承上的径向载荷和轴向载荷;X和Y分别为径向和轴向系数。
在(2)式中,没有考虑力矩的影响。实际上,如图1所示,力矩虽然不会改变径向载荷或轴向载荷的总量,但将改变轴承中钢球接触载荷的分布,从而降低轴承的寿命。

图1 钢球载荷分布
文中将考虑推力球轴承在轴向力和力矩作用下钢球的实际载荷分布,并用Lundberg和Palmgren的方法(简称L-P方法)计算轴承的疲劳寿命[2],在此基础上拟合出力矩与增量当量载荷之间的关系,从而在标准方法中计入力矩载荷的影响。
2 钢球接触载荷分布
在轴向力Fa和倾覆力矩M作用下,推力球轴承将产生轴向位移δa和转角θ。由于这两个位移,在位置角为φ的钢球处,内圈沟曲率中心Oi将相对于外圈沟曲率中心Oe产生轴向位移δai,如图2所示。

图2 推力球轴承变形与接触载荷

式中:Dpw为球组节圆直径;下标i表示第i个滚子(i=1,2,…,Z),Z为钢球数。假设接触角α不发生变化,则接触法向位移为:

由Hertz点接触理论,钢球接触载荷Qi为:

式中:K为刚度系数,由轴承的材料和几何参数确定[3]。轴承的平衡方程可表示为:

(6)式是以δa和θ为未知量的非线性方程组,求解它可以获得钢球接触载荷Qi。
3 基于钢球载荷分布的轴承寿命计算
早在1947年,Lundberg和Palmgen就在理论分析和大量试验研究的基础上提出了滚动轴承额定动载荷和疲劳寿命的理论[2]。这个理论经过一定的假设和简化演变成目前标准中给出的简洁的疲劳寿命计算公式。直至今日,这个理论的基本内容仍然适用,只是随着轴承材料和加工工艺的进步,对其中的部分内容做了修正和补充。
按照L-P理论,轴承套圈的额定寿命可表示为:

式中:Qc为套圈的额定动载荷;Qe为套圈的当量载荷。对于推力球轴承,套圈的额定动载荷可表示为:

式中:f为沟曲率半径系数;Dw为钢球直径;γ=Dwcosα/Dpw。(8)式中的上、下算符分别适用于内、外圈。当α=90°时,由于γ=0,γ/cosα=Dw/Dpw,于是(8)式变为:

对于相对于作用载荷旋转的套圈,其当量载荷Qeμ为:

因此,旋转套圈的疲劳寿命Lμ为:

对于相对于作用载荷静止的套圈,其当量载荷为:

因此,非旋转套圈的疲劳寿命为:

则轴承的基本额定寿命为:

这里分别采用L-P方法和标准方法计算某型号推力球轴承在Fa=20 000 N,M=300 000 N·mm作用下的寿命。已知Dw=22.225 mm,Z=16,Dpw=140 mm,α=90°,fi=fe=0.535,内圈旋转。
求解平衡方程(6)得到表1所示的结果。由于轴承受力对称,表中只列出了一半钢球的载荷。按照L-P理论得:

而按照标准方法计算,则:

对比计算结果可知,Ls比LLP高了约30%。显然,标准方法中不考虑力矩的影响是不合适的。

表1 钢球接触载荷
4 计入力矩影响的标准方法的修正
4.1 轴向载荷增量与力矩的关系
对于在轴向力和力矩作用下的轴承寿命LLP,总可以找到一个当量轴向载荷P′a,由它按(1)式计算寿命L′s=LLP。如图3所示,可以将P′a表示为:

式中:λ为增量载荷系数,λ=ΔFa/Fa;ΔFa是与M在寿命上相当的轴向载荷增量。

图3 力矩与其相当的轴向载荷增量
如果已知寿命LLP,则可根据寿命对等原则确定系数λ,从而可确定相应的当量载荷P′a。为此,令

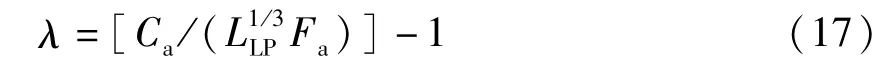
于是这样做必须首先求解平衡方程(6)获得钢球的载荷分布,因此是比较麻烦的。反过来,如果能找到λ与Fa和M的关系式,则可事先确定λ的值获得当量载荷P′a,然后就可按标准方法计算轴承的寿命。

式中:Qmax=K(0.5Dpwθsinα)1.5。

图4 力矩与钢球载荷
由力矩平衡方程得:


表2 λ计算结果

图5 M/(D pw F a)-λ曲线
4.2 标准方法的修正
可以根据载荷Fa和M,由(19)式确定λ,然后用(15)式确定P′a,则(1)式变为:

4.3 实例分析
例1,已知Ca=142 kN,用(20)式计算表1中的轴承在Fa=20 kN和不同力矩作用下的额定寿命,并比较与LLP寿命的相对误差ε。该计算结果如表3所示。

表3 L′s及ε的计算结果
例2,已知Dw=15.875 mm,Z=15,Dpw=85 mm,α=60°,fi=fe=0.535,内圈旋转;Fa=20 kN,M=150 kN·mm,分别用修正的标准方法和L-P方法计算轴承寿命,并比较二者的误差。
按照修正的标准方法,Ca=68.75 kN,P′a=21.18 kN;则L′s=34.2×106r。
按L-P方法得:LLP=35.0×106r。则相对误差ε=2.2%,两者计算结果相差不大。因此,用修正的标准方法可以很方便地准确计算出轴承的寿命。
5 讨论
由(18)式确定的仅在力矩作用下钢球最大载荷必须满足以下条件:

如果不满足以上条件,则圆周上只有部分钢球受载,这种情况对于推力轴承来说是不容许的。该式取等式时为轴承圆周上全部钢球受载的临界状态,如图6所示。

图6 圆周受载的临界状态
当轴承同时承受径向载荷时,情况将变得比较复杂,本文未考虑这种情况。

