自适应模拟退火遗传算法的改进与应用

邬 峰，黄丽亚

(南京邮电大学 电子科学与工程学院，江苏 南京 210003)

遗传算法GA(Genetic Algorithm)是一种随机搜索算法，1975年由 Holland[1]提出并发展起来，它具有隐含并行性和全局搜索性两大特点。其核心内容是参数编码、初始种群设定、适应度函数设计、遗传算子设计、控制参数设定。GA以一个种群中的所有个体为对象，利用随机化技术指导，对一个被编码的参数空间进行高效搜索。GA具有很强的计算能力，但是求解过程却很简单，因此成为现代有关智能计算中的主要算法之一。

模拟退火算法SAA(Simulated AnnealingAlgorithm)是1982年由Kirkpatrick[2]将固体退火思想引入组合优化领域，提出了一种求解大规模组合优化问题，特别是NP完全组合优化的有效近似算法。算法的核心在于模仿热力学中液体的冻结与结晶或金属熔液的冷却与退火过程。在搜索最优解的过程中，SAA除了可以接受最优解外，还有一个随机接受准则(Metropolis准则)，可以有限度地接受恶化解，并且接受恶化解的概率慢慢趋向于零，使得算法有可能从局部最优中跳出，尽可能找到全局最优解，保证了算法的收敛。

本文在分析这两种算法的长处与不足的基础上，将SAA引入到GA中，同时结合自适应调整遗传算法控制参数的思想对交叉变异算子进行自适应处理，提出了一种改进的自适应模拟退火遗传算法ASAGA(Adpative Simulated Annealing Genetic Algorithm)。仿真实验结果表明，该算法不仅可以提高解的精度，同时亦可获得较快的收敛速度。

1 遗传算法概述

遗传算法(GA)模拟了自然选择和遗传中发生的复制、交叉、变异等现象，从任一初始种群(Population)出发，通过随机选择、交叉、变异操作，产生一群更适应环境的个体，使群体进化到搜索空间中越来越好的区域，这样一代一代地不断繁衍进化，经过若干代之后，算法收敛于最好的个体(Individual)，很可能就是问题的最优解或次优解。

1.1 基本遗传算法

基本遗传算法SGA(Simple Genetic Algorithm)可定义为一个8元组：

其中，C为个体的编码方法；E为个体的适应度评价函数；P0为初始种群；M为群体大小；Ps为选择算子；Pc为交叉算子；Pm为变异算子；T为算法终止条件[3]。

SGA具体步骤描述如下：

(1)随机产生初始种群，个体数目一定，每个个体表示为染色体基因编码；

(2)计算个体适应度，判断是否符合优化准则。若符合，输出最佳个体或最佳解，并结束计算；否则转向第(3)步；

(3)采取比例选择法选择个体：根据适应度选择再生个体，适应度高的个体被选中概率高，适应度低的个体可能被淘汰；

(4)按照一定的交叉概率和交叉方法，生成新的个体；

(5)按照一定的变异概率和变异方法，生成新的个体；

(6)由交叉和变异产生新一代的种群，返回第(2)步。

SGA流程图如图1所示。

SGA一般在开始随机产生初始群体，然后不断地改进个体，以得到越来越好的结果。但由于收敛速度和寻找最优解往往是一对矛盾，SGA常表现为收敛速度慢、容易早熟、陷入局部最优解。

1.2 自适应遗传算法

利用遗传算法求解问题的关键是对问题的解进行编码，构造出适应度函数，并选取遗传算法参数：群体规模M、交叉概率 Pc以及变异概率Pm。其中，Pc和 Pm在遗传算法中的重要性已经得到研究者的公认。GA在搜索全局最优解时必须具备确定搜索最优解区域并收敛到最优解的能力及在搜索全局最优解时，开辟新的解空间的能力，这些特点是由Pc和Pm控制的。Pc取值越大，新个体产生的速度就越快，即开辟新的解空间的能力越强。然而Pc过大时遗传模式被破坏的可能性也越大，使得有高适应度的个体结构很快就会被破坏；但若Pc过小，会使搜索过程缓慢，以至停滞不前。对于变异概率Pm，如果取值过小，就不易产生新的个体结构；若 Pm取值过大，则GA就变成了纯粹的随机搜索算法。

针对GA所存在的问题，Srinivas[4]提出了自适应遗传算法，其思想是当种群适应度比较集中时，使交叉概率Pc和变异概率Pm增大；当种群适应度比较分散时，使Pc和Pm减小。Pc和Pm按如下公式进行自适应调整：

式中：favg为种群的平均适应度值，fmax为种群的最大适应度值，f′为交叉双方适应度较大者的适应度值，f为要变异个体的适应度值，0＜k1，k2，k3，k4≤1。

由上式可以看出，当适应度值越接近最大适应度值时，交叉率和变异率就越小；当等于最大适应度值时，交叉率和变异率为零。这种调整方法在群体进化后期比较合适，但对于进化初期不利。因为进化初期较优个体几乎处于一种不发生变化的状态，而此时优良个体未必是全局最优解，这容易使进化走向局部最优解的可能性增加。

为克服这些问题，保存群体中性能较好的个体，本文对参考文献[4]中自适应算子加以改进，新的交叉和变异概率计算表达式如下：

式 中 ：Pc1＞Pc2＞Pc3，Pm1＞Pm2＞Pm3， 它 们 的 取 值 在(0，1)之 间并在优化中调整。

2 模拟退火算法概述

模拟退火算法(SAA)是根据液态或固态材料中粒子的统计力学与复杂组合最优化问题的求解过程的相似之处而提出来的。统计力学论述了材料中相互作用的粒子的特性:不同的材料中粒子结构对应于不同的能量水平。如果用粒子结构或其相应能量来定义材料的状态，一个简单的数学模型可描述材料在温度T下从具有能量E(i)的状态i进入具有能量E(j)的状态j的机制：

若 E(i)≥E(j)，状态转换被接受；

若 E(i)＜E(j)，则状态转换以概率 p=exp{(E(i)-E(j))/KT}被接受，其中K为物理学中的波尔兹曼(Boltzmann)常数，T为材料温度。以上过程称为波尔兹曼接收策略。

SAA具体步骤描述如下：

(1)随机产生一个初始最优点，以它作为当前最优点，并计算目标函数值；

(2)设置初始温度：θ←T0；

(3)设置循环计数器初值：k←1；

(4)对当前最优点作随机变动，产生一个新的最优点，计算新的目标函数值，并计算目标函数值的增量Δ；

(5)如果 Δ＜0，则接受该新产生的最优点作为当前最优点；

如果 Δ≥0，则以概率 p=exp(-Δ/θ)接受该新产生的最优点为当前最优点；

(6)如果 k＜终止步数，则 k←k+1，转向第(4)步；

(7)如果未到达冷却状态，则：θ←T(k)，转向第(3)步；如果已经到达冷却状态，则输出当前最优点，计算结束。

以上步骤称为Metropolis过程。控制温度下降的函数的选取是SAA难以处理的问题。实际应用中，由于必须考虑计算复杂度的切实可行性等问题，常采用如下所示的降温方式:T(k+1)=λ×T(k)，式中 λ 为 正、略小于1.00的常数，k为降温的次数[5]。

按照一定的退火方案逐步降低温度，重复Metropolis过程，就构成了SA算法。当系统温度足够低时，可认为达到了全局最优状态。使用Meteopolis准则的优点是：当新解更优时，完全接受新解为新的当前解；而当新解为恶化解时，以概率p接受恶化解为新当前解。这就使得SAA能够保证局部寻优的精度，且还能够避免陷入局部最优[6]。

3 自适应遗传模拟退火算法

GA的局部搜索能力较差，但把握搜索过程总体的能力较强；而SAA具有较强的局部搜索能力，并能使搜索过程避免陷入局部最优解，但SAA对整个搜索空间的状况了解不多，不便于使搜索过程进入最有希望的搜索区域，从而使得SAA的运算效率不高[7]。但如果将上述两种算法相结合构成一种优化算法，则可互相取长补短，形成性能优良的全局搜索算法。在上述分析的基础上，本文提出了自适应模拟退火遗传算法(ASAGA)，不但使群体中的最优解得到了保留，同时避免了算法的早熟收敛问题，可以达到很好的全局寻优效果。

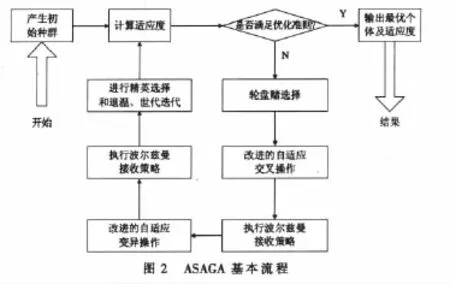
ASAGA设计的基本思想是：将SAA引入到GA中，构成一种混合算法，先是从一组随机产生的初始种群开始全局最优解的搜索，通过选择、自适应交叉及变异等遗传操作产生新一代种群，并对交叉和变异后产生的新个体实施波尔兹曼接收策略，然后再独立地对所产生出的个体进行精英选择操作[8]，以其结果作为下一代种群中的个体。这个运算过程反复迭代地进行，直到满足终止条件为止。在改进后的算法中，GA侧重于全局搜索，SAA侧重于局部搜索，两者的结合将使算法的效率大大提高。

ASAGA算法步骤可描述如下：

(1)设置初始参数，包括种群规模M，最大迭代次数Tmax，交叉概率 Pc和变异概率 Pm，以及退火初始温度 T0，温度冷却参数λ；

(2)初始化种群，按随机方法产生初始群体中的每个个体，得到初始种群；

(3)计算种群中个体的适应度值，评价是否满足终止条件。若满足，则输出最优解，终止算法；否则进入步骤(4)；

(4)采取比例选择方法选择个体，对被选中染色体进行交叉操作，其中的交叉概率通过式(3)计算得出。计算交叉产生的子个体所对应适应函数值 f(x′)，仅在min{1，exp((f(x)-f(x′))/Tk)}＞random 条件下接收新解，其中f(x)为父代个体适应度值，Tk为当前温度，random是(0，1)之间的随机数；

(5)对交叉后的染色体进行变异操作，其中变异概率通过式(4)计算得出；同理，按步骤(4)中的方法决定是否接收变异后的解；

(6)进行世代和退火降温的迭代，温度变化按照公式：Tk+1=λ×Tk，k←k+1，λ∈(0，1)，同时进行精英选择：把进化过程中出现的最优个体直接复制到下一代中，替换下一代中适应度差的个体，并令被复制个体不参加任何遗传操作。计算后，转向步骤(3)。

自适应SAGA基本流程如图2所示。

4 实验仿真

为测试本文提出的ASAGA的全局寻优性能，选取一个典型的多峰值函数作为测试函数，用MATLAB语言进行仿真，寻找其全局最优解，并与SGA求解此函数全局最优解的结果相比较。设：

该函数在 x∈(0，9)区间中的最大值为 24.855 4，全局最优点在x=7.856 9左右。

SGA采用的遗传操作及相应参数为比例选择、单点交叉(Pc=0.85)及基本位变异(Pm=0.05)，种群规模 M=20，最大迭代次数Tmax=40。

SGA仿真结果如图3所示。

ASAGA 相 应 参 数 设 置 如 下 ：Pc1=0.4，Pc2=0.3，Pc3=0.2；Pm1=0.2，Pm2=0.1，Pm3=0.05；T0=100，λ=0.95；种群规模M=20，最大迭代次数 Tmax=40。

ASAGA仿真结果如图4所示。

通过对比图3、图4的仿真结果，可以看出：由于SGA的交叉变异概率在进化过程中没有变化，导致不同个体的交叉变异操作是相同的，算法在第12代就陷入局部最优点，直至最大迭代数也没有跳出来。而ASAGA在全局寻优能力、收敛概率和收敛速度等方面明显优于SGA。ASAGA确定的自适应交叉、变异概率具有很强的指导搜索方向的能力，算法在第7代就迅速寻到了全局最优点，达到了既快又好的效果。表1给出了两种算法运算结果中关键参数的对比。

表1 SGA和ASAGA运算结果比较

本文在分析了遗传算法的优缺点的基础上，提出了一种融入了模拟退火算法的混合遗传算法——自适应模拟退火遗传算法。将模拟退火算法和遗传算法有效地结合，同时改进自适应遗传算子，实现了两者的优势互补。仿真结果表明，改进后的自适应模拟退火遗传算法可以显著提高遗传算法的寻优性能和运行效率，较为有效地克服了基本遗传算法易早熟和容易陷入局部最优解的缺点。

[1]HOLLANG J H.Adaptation in natural and artificial systems[M].Ann Arbor:University of Michigan press，1975.

[2]KIRKPATRICK S， GELATT C D， VECCHIM P.Optimization by simulated annealing[J].Science， 1983，220:671-680.

[3]陈国良，王煦法.遗传算法及其应用[M].北京：人民邮电出版社，1996.

[4]SRINIVAS M，PATNAIK L M.Adaptive probabilities of crossover and mutation in genetic algorithms[J].IEEE Trans System， Man and Cybernetics， 1994，24(4):656-667.

[5]王小平，曹立明.遗传算法—理论、应用与软件实现[M].西安：西安交通大学出版社，2002.

[6]康立山，谢云，尤矢勇，等.非数值并行算法(第一册)—模拟退火算法[M].北京：科学出版社，1995.

[7]王凌，郑大钟.一种GASA混合优化策略[J].控制理论与应用，2001，18(4):552-554.

[8]李敏强，寇纪淞，林丹，等.遗传算法的基本理论与应用[M].北京：科学出版社，2002.