电容层析成像图像重建算法研究

刘传美

(北方工业大学 机电工程学院自动化系，北京 100144)

电容层析成像(ECT)技术是基于电容敏感原理的过程层析成像技术，运用传感器阵列形成旋转的空间敏感场，从不同的观测角度获得被测物场的介电常数分布信息，利用图像重建算法，显示被测物场的二维或三维介质分布图像。

典型的ECT系统结构主要由3部分构成：电容阵列传感器、数据采集系统和成像计算机。其基本原理是：位于管道内具有不同介电常数的两相流在流动时，各相含量和分布不断变化，引起电容传感器不同极板间的电容值改变。通过均匀安装在绝缘管道外壁的电容传感器检测出各电极间的电容值，送至数据采集系统。数据采集系统将这些电容值转化为数字量并传送给成像计算机，根据某种图像重建算法重建出流体在截面的分布图像。

1 ECT系统图像重建算法

ECT系统图像重建是一个逆问题，即通过有限个电容测量值将成像区域内的介电常数空间分布图重建出来。由于电容层析成像系统本身固有的“软场”特性，且能得到的独立电容测量值数量非常有限，逆问题不存在解析解，图像重建的难度较大。

针对目前图像重建算法在成像质量和成像速率上存在的问题，本文提出一种基于QR分解的电容层析成像算法。该方法首先将ECT物理模型进行规范化和Tikhonov正则化处理后，进而将QR分解的思想引入ECT方程的求解中实现图像重建。

1.1 ECT系统的数学模型

ECT技术图像重建可描述为两大内容：一是正问题的建模，二是逆问题的求解。ECT系统的正问题模型为[1-2]：

式中，i、j分别表示源电极和测量电极的编号，D表示管道横截面积，ε(x，y)表示管道内电介质的分布函数，Si，j[x，y，ε(x，y)]为极板电容 Ci，j的分布函数，即 Ci，j对点(x，y)处的电介质的敏感程度。

对式(1)进行离散化和线性化处理，可得到矩阵表示的 ECT系统的正问题模型[1，3-4]：

C为归一化的电容值；G为归一化的介电常数分布，即像素的灰度值；S为归一化的灵敏度矩阵。需要指出的是，式(2)是经过降质处理的简化模型，用它求解逆问题进行图像重建时必然会带来误差，需要对图像进行修正。

1.2 正则化求解系统逆问题

病态逆问题往往是由于缺乏足够的信息而导致的。正则化方法的原理是找到一个由先验信息约束的解集，然后再从中选择1个解。一个ECT系统经过降质处理的正问题的线性化模型如式(2)，是一个病态逆问题求解，而Tikhonov正则化方法是一种应用最普遍的解决病态逆问题的方法。

ECT系统的逆问题就是通过获得的电容测量值去重建介质在检测区域内的介电常数分布图。由于像素个数(文中区域划分为 1 780个)多于观测数据(文中是28个电容测量值)，对于式(2)而言是未知数大于方程个数，是个欠定方程，具有无穷多个解，但有最小二乘最小范数解，因此逆问题模型可以表述如下[5]：

式中，S+为观测矩阵 S的广义逆；G+为 G的最小二乘解，即重建的图像灰度值的估计值。用广义逆求解逆问题具有不适定解，测量数据的微小波动将引起解的较大变化，导致解不稳定。消除这种解不稳定的有效方法之一是采用正则化法。Tikhonov在研究第一类Fred Holm方程时提出了一种正则化算法，这种算法对于每一个正则化参数使下面的泛函达最小[6-7]：

式中，μ为正则化参数，D为降质算子，f为被测信号，g为观测信号。

对应于ECT系统，式(4)使泛函变为：

达最小，即令：

则对于 μ＞0，有正则化解：

SR=(STS+μI)-1ST为Tikhonov正则化广义逆，是一个(1 780×28)维矩阵；I为单位矩阵。正则化参数μ控制着正则化先验知识与测量数据的权重，其取值非常关键，理论上确定μ的大小很困难，通常要根据试验设定。

1.3 基于QR分解的图像重建算法

正则化虽然能使方程系数矩阵的条件数大大降低，但这只是在一定程度上改善了系数矩阵的病态性，方程解的熟练依旧需要较高的迭代次数，因此不能满足过程成像的实时性要求。为此，在此基础上提出了基于QR分解[8]的图像重建算法。

当矩阵条件数较大时，求逆矩阵计算精度不高。为避免对(STS+μI)直接求其逆矩阵可采用先对其求QR分解然后再进行求解。

基于QR分解的图像重建算法是利用经过正则化后对(STS+μI)进行 QR分解，求出初始图像灰度值的估计值，再根据正问题计算出初始图像的电容值，将计算电容值和实际测量值相比较得出1个电容偏差值，再利用QR分解的方法求出相应于电容偏差值的偏差图像，然后进行修正。

具体实现过程如下：如前所述，经Tikhonov正则化后可得到：

因为(STS+μI)是一个(1 780×1 780)方阵，所以可以进行QR分解，即把它分解为1个正交矩阵Q和1个上三角矩阵R的乘积，即：(STS+μI)=QR。通过求解可以得到G的解为：

根据QR分解算法对初始图像进行修正，可以得到修正后的图像模型为：

式中，GQR为基于 QR分解的初始图像，即式(9)，β为优化修正因子，△G为偏差图像：

C为由ECT正问题模型式(2)得的初始电容值。

求解优化修正因子 β[9]：

根据ECT正问题模型式(2)得修正后电容值为：

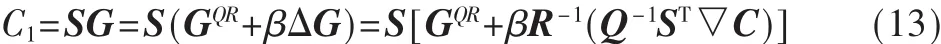
与初始测量电容值比较得电容值误差向量▽C1：

式中，C1为修正后图像测量值，即为根据正问题计算出的初始图像的电容值。

构造函数f为：

由式(14)可知，f是 β的函数，求 β的最优解，就变成使f最小的问题，即求修正因子β，使得电容值误差向量的模最小。为此，对f求导并令其等于零，即：

即：

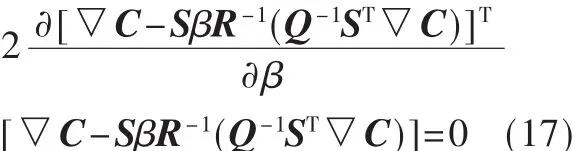
经过求解可得到的表达式为：

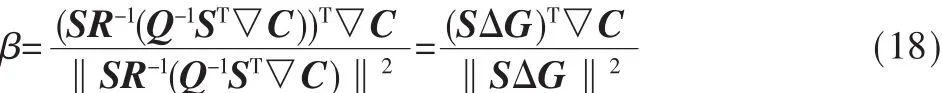
2 成像结果分析

对线性反投影(LBP)法[1]、迭代法[4]、Tikhonov 正则化法、正则化修正算法(ROR)[9]和基于QR分解的重建算法5种图像重建算法的重建图像速率和图像质量进行了比较。成像传感器采用8极板结构，校验用管壁的介电常数为2(满管为2.5)，用尼龙测试棒进行实验测试。

重建图像速率用迭代次数die_num表示，die_num越大则重建时间越长，说明速率越低。由于LBP法、正则化法对数据的处理过程是一样的，都属于单步处理，所以die_num=0；而ROR法和基于QR分解的重建算法的整个数据处理过程是在单步数据处理的基础上增加了1步修正过程，相当于迭代1次，即die_num=1。

重建图像质量采用目前常用的评价指标占空比[1-2，4，10]表示。占空比表示图像面积占整个成像区域面积的百分比，表示为：

Area1为高介电常数部分图像面积，Area为成像区域面积。成像效果图如图1所示。表1给出了不同图像重建算法所重建图像占空比和重建时间的对比结果。

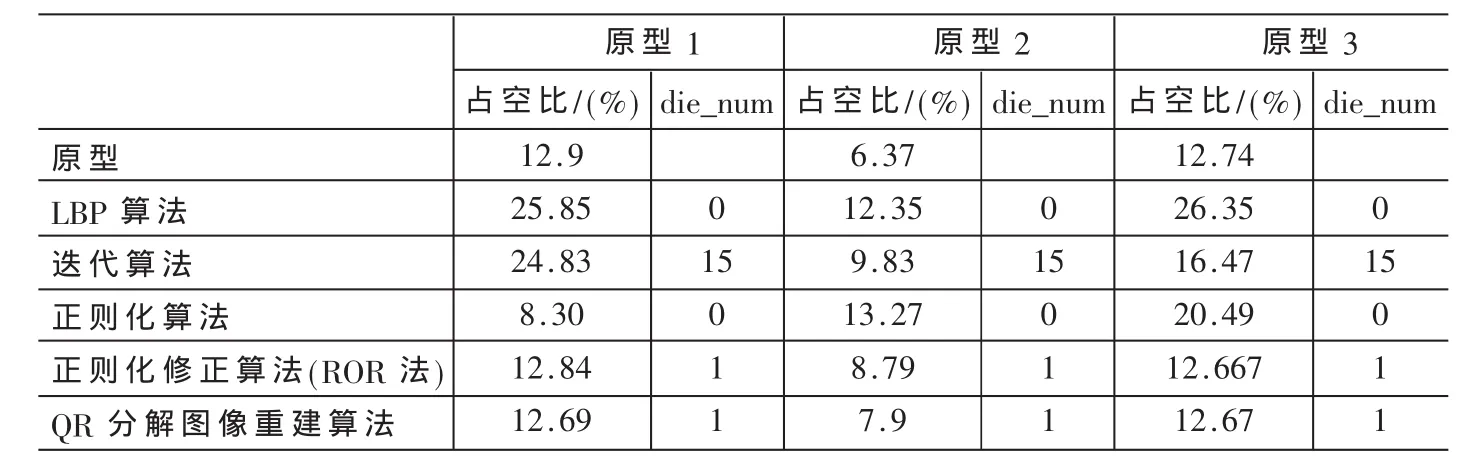
表1 不同图像重建算法所重建图像占空比和重建时间

从表1可以看出：

(1)LBP法和正则化法是单步算法，重建图像时间最短即速率最快但是偏离实际原型太大。

(2)迭代算法迭代10次之后的结果与LBP法和正则化法相比，比较接近实际原型，但是重建时间太长。

(3)从重建图像时间看，ROR法和QR分解图像重建算法仅为迭代法的1/15，而QR分解图像重建算法所重建图像的占空比，比ROR法更接近成像原型。

由图1可以看出：基于QR分解的电容层析成像算法图像重建结果最为接近真实物体，图像质量得到改善。综上成像实验结果表明：基于QR分解的图像重建算法图像重建结果与实际原型较接近，优于其他几种算法。

本文在正则化的基础上提出的基于QR分解的图像重建算法，通过与当前常用的线性反投影(LBP)法、迭代法、Tikhonov正则化法和ROR法的成像实验对比，从占空比和图像重建时间两方面可以表明，用该算法得到的图像具有比较好的图像重建质量和较高的成像速率。

[1]XIE C G，HUANG S M.Electrical capacitance tomography for flow imaging-system model for development of image reconstruction algorithms and design of primary sensors[J].IEEE Proc.G.1992，139(1):89-98.

[2]XIE C G，BECK M S.8-electrode capacitance system for two-component flow identification， Part1；tomographic flow imaging [J]. IEEE Proc. A，1989，136(4):173-183.

[3]ISAKSEN O.A review of reconstruction techniques for capacitance tomography[J].Meas.Sci.Technol.1996(7):325-337.

[4]YANGWQ， SPINKDM，YORK T A，et al.An imagereconstruction algorithm based on land weber’s Iteration method for electrical-capacitance tomography[J].Meas.Sci.Technol.1999(10):106-1069.

[5]KUHNERT F.广义逆矩阵与正则化方法[M].陈杰，译.北京:高等教育出版社，1984.

[6]TIKHONOV A N，ARSENIN V Y.Solution of Ill-posed problems[C].New York:John Wiley，1977.

[7]王延平.信号复原与重建[M].南京:东南大学出版社，1992.

[8]刘会灯，朱飞.MATLAB编程基础与典型应用[M].北京:人民邮电出版社，2008.

[9]赵进创.正则化优化修正的电容层析成像图像重建算法[J].仪器仪表学报，2004，25(1):1-4.

[10]TAPP H S，KEMSLEY E K.Image improvement in softfield tomography through the useofchemo metrics[J].Meas.Sci.Technol.，1998(9):592-598.