也谈交点速度问题的解法

郑 金

(辽宁省凌源市职教中心,辽宁凌源 122500)

本刊2009年第5期刊登了“常见的速度合成问题错解分析”一文,2009年第11期刊登了“对两类速度合成问题错误的再分析”一文,都对交点类、关联类的速度求解问题进行了详尽分析并给出正确的解答方法,读后颇受启发.由于交点速度问题比关联速度问题相对较难且生疏,并具有一定的教学价值,因此本文将对这类问题进行专题探究.所谓交点速度问题,一般是指在同一平面内相交放置的直杆与直杆、圆环与圆环或直杆与圆环,当发生匀速直线运动或匀速圆周运动时,其交点将发生某种运动.若已知直杆和圆环运动的速度,则可求交点运动的速度.对于这类问题的解答,除了速度合成分解法、位移微元法外,还有一种通法,即解析式求导法,下面进行分析.

例1.如图1所示,临界角为45°的液面上有一点光源S发出一束光线,垂直入射到水平放置于液体中且距离液面为d的平面镜M上.当平面镜 M绕垂直过中心O的轴以角速度ω逆时针匀速转动时,观察者发现水面上有一光斑掠过.设t=0时平面镜处于水平位置且镜面向上,试确定观察者所观察到的光斑在水面上移动速度v与时间t的函数关系式.

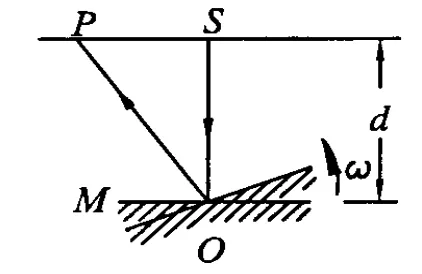
图1

图2

解法1:端速分解法

把光线视为运动的直杆,绕轴 O转动;把水面上光线经过的路径视为静止的直杆,它们的交点沿着水面移动.经过时间 t,平面镜转过的角度为 θ=ω t,光线反射到水面上的P点,由于点O到水面的距离不断增大,则光线在转动的同时,长度还增加,因此可将光斑沿水面的速度分解为沿着光线方向的纵向速度v∥和垂直于光线方向的横向速度v⊥,如图 2所示.

解法2:解析式求导法

建立直角坐标系如图3所示,可知点P的横坐标为x=dtan2θ=dtan2ω t,对时间求导数,得速度

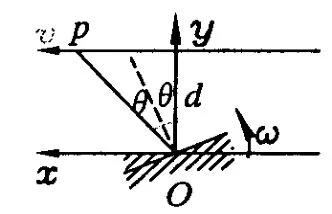
图3

例2.如图4所示,两根细长棒 AB与CD夹角为θ,分别以垂直于自身的速度v1与v2移动,求交点M 的移动速度.

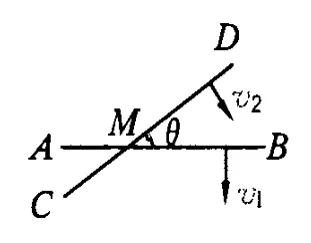
图4

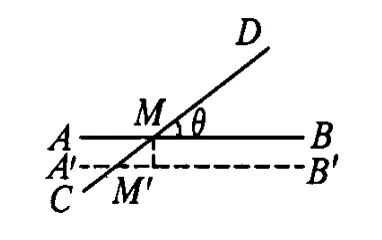
图5

解法1:速度合成分解法

设杆CD不动,只有杆AB移动,则交点沿着杆CD运动,如图5所示.分解速度 v1,沿着杆CD运动的速度为v1′如图6所示.

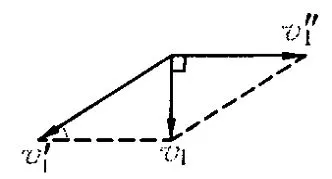
图6

设杆 AB不动,只有杆CD移动,则交点沿着杆 AB运动,如图7所示.

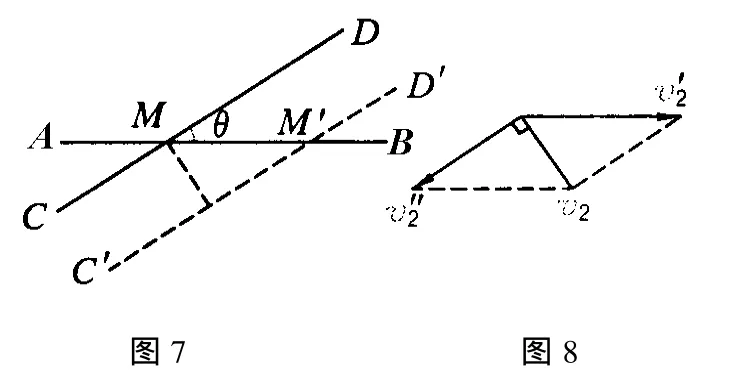
分解速度 v2,沿着杆 AB运动的速度为如图8所示.

由图6和图8可知,分速度 v1′与v2′所成角度为180°-θ,由余弦定理得交点 M的合速度为

解法2:解析式求导法

建立如图9所示直角坐标系,在t=0时刻,两根直杆的交点位于坐标原点,则在任意时刻t,直杆 AB的直线方程为

直杆CD的直线方程为

由方程(1)、(2)可得任意时刻交点的坐标为

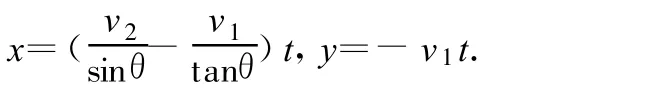
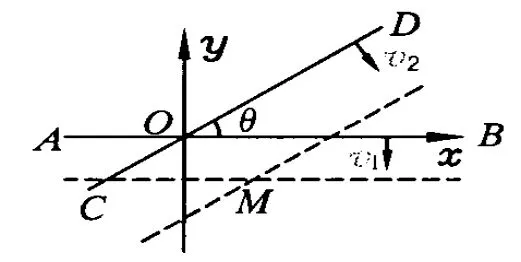
图9

这就是交点的参数方程,表明交点沿坐标轴方向做匀速直线运动,交点沿坐标轴方向的速度分量分别为

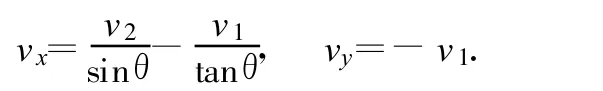
所以合速度为

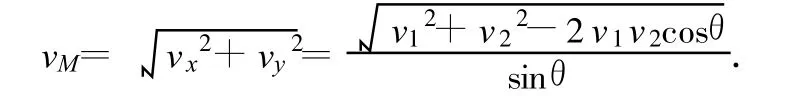
例3.如图10所示,一个半径为 R的轴环O1立于水平面上,另一个同样的轴环O2以速度v从这个轴环旁通过,试求两轴环上交点A的速度vA与两环中心之距离d的关系.轴环很薄,且第2个轴环紧傍第1个轴环通过.

解法1:沿杆同速法

在轴环O2以速度v运动的过程中,因交点到圆心 O2的距离即半径保持不变,则半径 AO2的运动相当于轻杆的运动,其两端点的运动速度分别等于圆心O2和交点的运动速度.交点相对于地面的速度vA沿静止环的切线方向,与半径 AO2的夹角为如图 11所示.

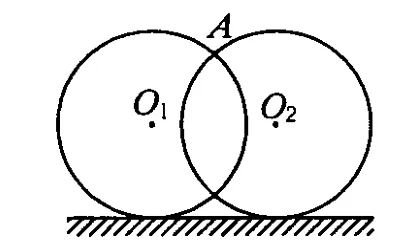
图10

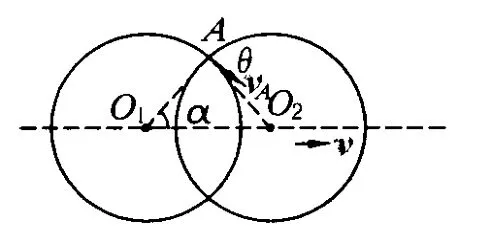
图11

在同一时刻,半径 AO2两端点的沿杆的纵向分速度相等,即“沿杆同速”,可知 vcosα=vAcosθ,即 vcosα=vAsin2α,则

解法2:解析式求导法

建立直角坐标系如图12所示,若从两轴环重合时开始计时,则在任意时刻t两圆心之间的距离为d=vt,因轴环O1的圆心位于坐标原点,则轴环O1所在圆的方程为

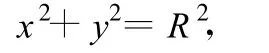
轴环 O2的方程为

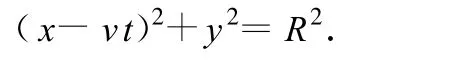
由此可得

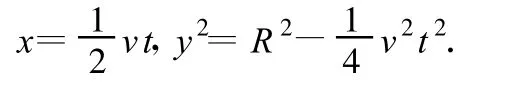
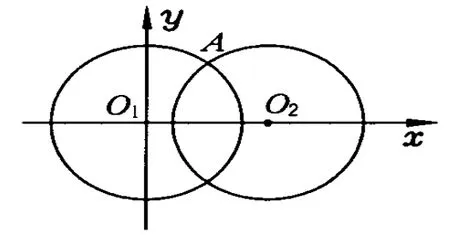
图12

此即为交点 A的参数方程.

分别对时间求导数得

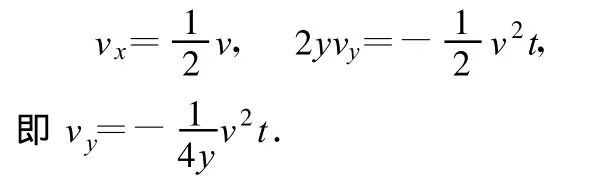
已知 d=vt,还有几何关系

可知合速度的平方为

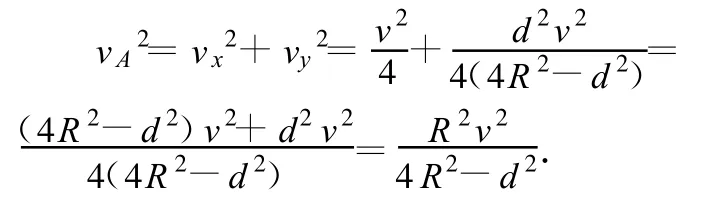
所以合速度即交点 A移动的速度为

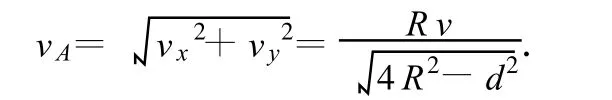
因d=vt为变量,故交点A的速度随时间而变化.

综上可见,对于交点速度问题,解法多样,而利用解析法和导数知识来求解,数理相结合,妙趣横生.

1 郭明远.解运动合成与分解题的思路.中学物理(高中版),1999(12).

2 刘玲.常见的速度合成问题错解分析.物理教师(高中版),2009(5).

3 周栋梁.对两类速度合成问题错误的再分析.物理教师(高中版),2009(11).

4 黄晶.陈题新解温故知新.中学物理(高中版),2009(3).

5 姚昌新.利用解析法求交点速度.中学物理(高中版),2009(10).