仅自变量可重复观测的变系数线性结构型EV模型的参数估计

周跃进 ，陈桂景 ，王 蕊

(1.安徽理工大学 理学院，安徽 淮南 232001；2.安徽大学 数学科学学院，合肥 230039)

0 引言

在许多实际问题中，EV模型的系数往往是随时间等因素变化而变化，并且在EV模型研究中一般都对模型误差方作某种约束，这往往带有主观性。但在一定条件下可作重复观测，利用其结果对误差方差作估计，从而可以避免对其施加人为的约束。在实际问题中，有时只允许模型中自变量可重复观测。如在农业实验中，实验田划分为若干个大地块，以x记地块的肥力，它实际上是该地块上肥力的平均值，而我们只能从该地块各处取样测x，所得结果构成对x的重复观测。但如因变量Y表示地块的单产量，其值一般只需测量一次。这类问题具有一定的普遍性。刘继学在文献[4]中研究了仅自变量有重复观测时常系数线性EV模型的参数估计。本文考虑只允许自变量有重复观测的变系数结构型线性EV模型。

假设在参变量t处自变量x与因变量y满足一元线性关系

这里x,y是随机变量，t是参变量；a(t)，b(t)是t的连续函数且 b(t)≠0。

假定 t1,t2,…，tn,是[0，1]上的 n个设计点，在每个 ti处对作重复观测，获得样本观测值(ti,Xij,Yi)；i=1,…，n；j=1,…，ni。 其中Xij,Yi为真值xi,yi的观测值，xi,yi是不能直接观测的随机变量。本文模型是

其中对模型作如下基本假定：

(1)x1,x2,…，xn是随机变量的iid真实值,EX,EX2存在；

(2)uij（i=1,2,…，ni）为 iid,且

(3),e1,e2,…，en为 iid,且

(4){xi}，{uij}和{ei}相互独立。

在模型（2）中，令 a(t)=a、b(t)=b、a、b 未知，即为文献[4]中所研究的问题。本文感兴趣的是估计模型（1.2）中变系数a(t).

b(t)在t=t0∈(0，1)处的值 a(t0)、b(t0)和本文利用重复观测数据和局部加权的方法，构造出参数a(t0)、b(t0)和测量误

1 a(t0)、b(t0)和的估计

文献[5]对变系数线性结构关系EV模型的参数a(t0)、b(t0)采用加权正交回归最小二乘的方法获得其估计量。如果用文献[5]中的方法，则考虑样本点(Xij,Yi)到(t0-hn,t0+hn)内的局部回归直线y-b(t0)x-a(t0)=0的正交距离平方加权和

达到最小为原则来估计 a(t0)、b(t0)，求出 a(t0)、b(t0)的估计量但由于未必相等，因而不再收敛到 b(t0),因此必须采用另外的估计方法。本文利用t0处重复观测值(ti,Xij,Yi)来估计 a(t0)、b(t0)和首先利用重复观测数据对进行估计，然后利用局部加权方法估计和

如果 Wni(t0)满足(1)，权函数。

关于权函数的选择，可先选定适当的有界概率密度函数K(x),称之为核函数;然后选定窗宽hn∈(0,1/2)。由事先确定的设计点 0≤t1＜t2＜…tn≤1 及 t0∈(0,1),构造权函数：

一般窗宽hn随n增大而减小，理论上hn满足当n→∞时，n→0，nhn→∞。

本文采用以下记号：

2 主要结果

条件保证了[0，1]内的n个设计点不能过于聚集在某点附近。在一些假定条件下，本文得到如下主要结果。

假定设计点 0≤t1＜t2＜…＜tn≤1，且满足：

3 定理证明

为了证明定理的结论，需引入下列引理。引理 1[6]在(5)式定义下，

引理 2[5]设随机变量 ξ,ξ1,ξ2…，ξniidEξ,Eξ2存在，随机变量e1,e2,eniid，Ee1=0,Ee2=σ2<∞有界县在t0附近连续。若→∞(n→∞)，则当n→∞时：

引理 3[5]设随机变量 ξ,ξ1,ξ2…，ξn，相互独立，随机变量e1,e2,en相互独立有界且在 t0附近连续。若则当n→∞时：

引理 4[5]设随机变量 ξ,ξ1,ξ2…，ξniidEξ,Eξ2存在，随机变量 e1,e2,eniid，Ee1=0,Ee2=σ2<∞，f(t)有界县在 t0附近连续。 若则当n→∞时：

引理 5[5]设随机变量 ξ,ξ1,ξ2…，ξn相互独立，随机变量e1,e2,en相互独立,f(t)有界且在 t0附近连续。若则当n→∞时：

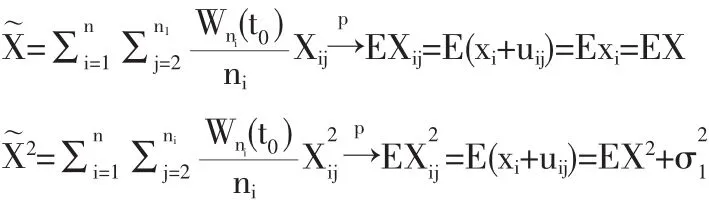
由引理2和引理3知

再由引理2和引理3有：

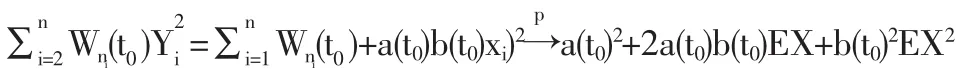
再讨论S2XY的收敛性。

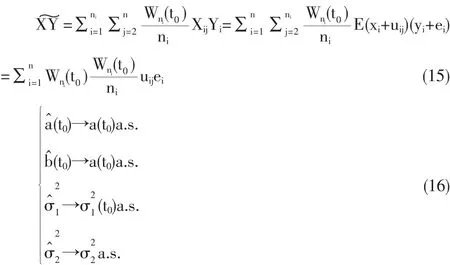
由引理3可得：

由(10)、(11)、(14)、(17)式,可得到

由此，定理得证。

由引理4和引理5，同理可证得定理2。

[1]Wang Qihua.Estimation of Linear Error-in-Covariables Models with Validation Data under Random Censorship[J].J Multivariate Anal.,2000，(73).

[2]ZhangS.G.,Chen X.R.Consistency of Modified MLE in EV Model with Replicted Observations[J].Science in China(Series A),2001,44(3).

[3]Zhang S.G.,Chen X.R.Asymptotic Normality of Parameters Estimation in EV Model with Replicated Observations[J].Acta Mathematica Scientia(Series B),2002,22(1).

[4]Liu J.X.,Zhang S.G.,Chen X.R.EV Models with Replicable Observed Independent Variables[J].Science in China(A),2006,36(5).

[5]Ou Y.G.On Parameter Estimation for Linear Varying-coefficients Structural EV Models[J].Acta Mathematicae Applicatae Sinica,2005,28(1).

[6]Zhang S.G.Research about EV Models PhD[D].Paper,2002.

[7]Stout W F.Almost Sure Convergence[M].New York:Acadamic Press,1974.