船闸通过能力分析中的几个问题探讨

廖 鹏

（东南大学港口航道与水利工程研究所，南京210096）

当船闸提供的通过能力无法满足船舶过闸需求时，容易出现滞航或堵航现象，往往成为内河航道的控制节点、甚至是瓶颈口，影响着整个水运交通网络的运输能力［1］。因此在内河航道（网）规划与评价、船闸规划与设计中，船闸通过能力分析尤为重要。在大中型通航船闸的研究、设计和建设方面，我国已取得了巨大的成就，但在分析和计算其通过能力时，往往忽略了船舶过闸时可能出现的延误（或待闸时间）以及由此产生的经济损失，导致船闸的规划、设计与调度管理存在诸多不合理的现象［2］。

船闸通过能力分析是通航枢纽的交通规划问题，既要考虑船闸所能通过的船舶数量以充分发挥其运输功能，又要将船闸视为一个服务节点而关注船舶和货物是否及时、安全地通过船闸，也就是说船闸通过能力不仅是船闸通过船舶数量的表达，也是船舶通过船闸质量的描述［2］。船闸的通过能力分析不仅要计算船闸通过船舶的数量，也要评价船舶通过船闸的服务质量感受（如过闸时的延误、船员感受等）。据此理念，本文综合阐述了船闸通过能力分析中的几个关键问题［1-5］，并探讨了如何构建船闸服务质量的评价体系。

1 研究回顾

早在20世纪四、五十年代，前苏联和美国学者根据船闸运行的特点，提出了船闸通过能力的计算方法，认为船闸的理想通过能力等于每年实际运行天数中每天过闸次数与一次过闸平均吨位的乘积的总和，实际通过能力等于最大能力除以高峰月通过能力与平均月通过能力的比值［6-7］。稍后，美国学者发现船闸的服务对象更关心的是船舶和货物能否及时、安全地通过船闸，而不是船闸通过的货物总吨位。因此，应用当时兴起的排队理论，研究分析船舶的到达分布和服务时间分布，将船闸视为1个或2个服务窗口（单线或双线船闸）的排队系统，研究船舶的延误［8-9］。采用标准统计分布函数来描述船舶到达和服务时间规律并不具有普遍性，因而更具普遍性的G/G/n排队模型被广泛采用［10］。不过，考虑诸多控制因素的G/G/n模型的求解非常复杂，难以得到明显的表达式，故常用近似简单的模型去逼近或是数字仿真直接求其数值解。由此，数字仿真模型被用来模拟船舶的延误，以便更准确地描述航道网交通流的复杂性［11］。

采用排队理论研究延误是为了给船闸的调度管理提供决策依据［12］，或是为船闸和航道网规划及建设的经济评价提供基础数据［13］。基于大量的实测数据和基础研究，船舶延误研究的对象从点（单级单线船闸和多线船闸）到线（梯级船闸和航道）再扩展到面（航道网），为航道网改扩建工程的规划与评估提供了较可靠的数学模型［14-15］，并成功应用于上密西西比河——伊利诺斯水道扩建工程可行性研究中［16］。总的来说，经过近50年的努力，初步建立了内河水运交通规划与管理的基础理论和数学模型，为解决内河水运工程问题提供了大量的技术支持，有力地促进了美国综合交通运输的发展。

我国的船闸通过能力研究延续了前苏联的办法，在计划经济体制下，强调充分发挥船闸的经济效益，注重分析船闸通过船舶的数量，而忽略了船舶过闸时的延误。《船闸总体设计规范》（JTJ305-2001）［17］（以下简称规范）推荐的船闸通过能力计算方法如下

式中：P1为单向年过闸船舶总载重吨位；P2为单向年过闸客、货运量；n为日平均过闸次数；n0为日非客运、货船过闸次数；N为年通航天数；G为一次过闸平均载重吨位，结合设计船型与闸室有效尺度进行组合来确定；α为船舶装载系数；β为运量不均衡系数，为1 a中最大月货运量与年平均月货运量的比值。长期实践表明，该方法概念清晰，公式结构简单，一定程度上能够满足工程需要。随着近年来货运过闸需求快速增长，大型船闸的建设并投入使用，实践中遇到的许多问题逐渐受到各方的关注。有学者开始对通过能力的计算方法进行探讨［18-19］，另一方面，为提高船闸的通过能力，缓解船闸的堵航程度，开始应用数学模型来优化船闸调度工作［20-22］。

2 船舶平均待闸时间

时间延误是衡量交通系统服务质量的重要指标，也是指导交通设施规划和建设的重要依据［23］。由于种种原因，国内缺乏系统的船闸运行实测数据，相关的文献报道非常少。下面据京杭运河施桥船闸的实测数据［2］，提出繁忙船闸的船舶待闸时间的估算模型。

2.1 平均待闸时间分布特性

根据施桥船闸2001～2004年共约117.8万艘次单机船和驳船的待闸时间资料，采用小时为单位，将船舶待闸时间按间距2 h分成若干等级，统计每个等级所出现的船舶数，计算其对应的比例，绘出船舶待闸时间的分布图。限于篇幅，图1仅给出了该断面全部过闸船舶的待闸时间分布。

可以看出，尽管影响船舶待闸时间的因素较为复杂，但其仍有规律可循：（1）船队的待闸时间主要分布在16 h以内，其中2 h以内的船队比例约34%，不待闸的船队比例最大可达12%；（2）单机船的待闸时间主要分布在6 h以内或者14～22 h，2个待闸时间区间平均相差约10 h，主要是因为部分单机船夜间不过闸），分别占67%和28%，其中在2 h以内的平均约占40%，不待闸的单机船比例仅约4%。

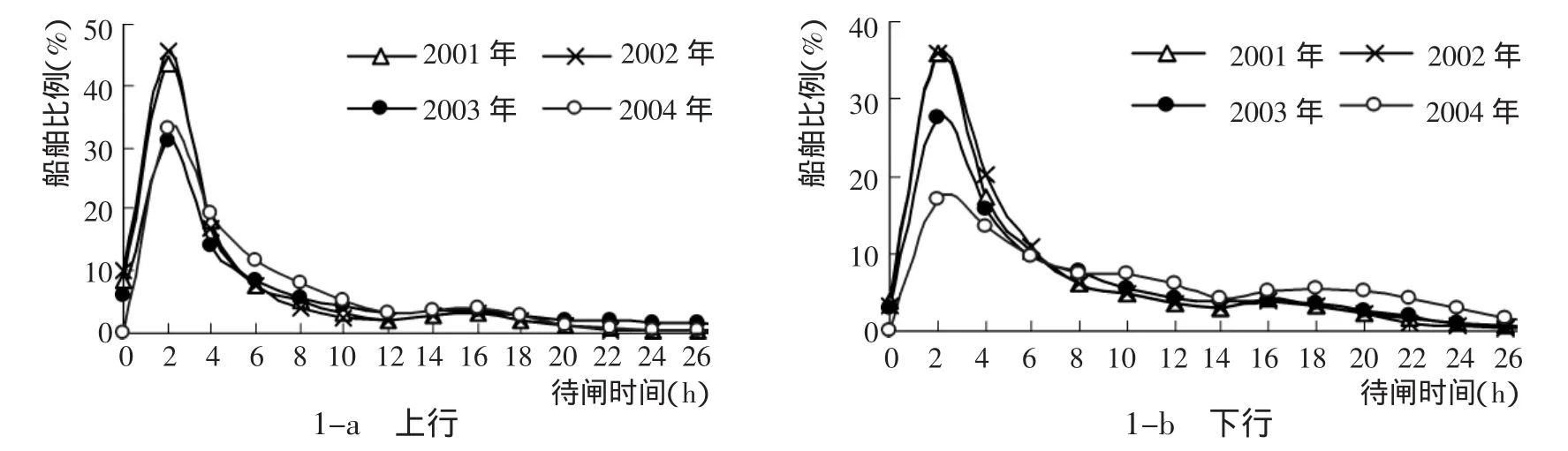
图1 施桥船闸的船舶待闸时间分布Fig.1 Distribution of delays at Shiqiao lock

从年际间不同流向船舶来看，下行船舶的待闸时间较上行船舶的长，而且船舶的待闸时间总体上在逐年增加，尤以2004年下行船舶的增幅最大。例如，2001～2004年下行船舶待闸时间在20～40 h的比例分别为4.8%，3.1%，6.8%和13.6%。这主要与船闸不同航向上的年船舶通过量有关，通过量越大，即交通负荷越大，船舶的平均待闸时间就可能越长。2003年的船舶待闸时间较长主要与船闸7月份的停航有关。

2.2 平均待闸时间的估算模型

采用船舶到达和服务时间均为一般分布的G/G/n排队模型来研究船舶的待闸时间。单线船闸可采用G/G/1模型，双线船闸一般采用G/G/2模型。我国多数双线船闸的尺度接近并进行联合调度，为简化问题，可将船闸的2个闸室看作1个统一的大闸室（如施桥船闸），或者因船闸的调度原则可看作单线船闸（如三峡船闸的北线上行、南线下行），统一采用先到先服务的G/G/1模型来研究船舶的待闸时间。

定义船舶到达的间隔时间序列独立、服从一般分布F（t），令平均到达间隔时间为；船舶一次过闸时间序列独立、服从一般分布G（t），t≥0，记平均一次过闸时间为。若令 Wq，m为第m条船舶的待闸时间（排队等候时间），Wq（t）为系统平衡时船舶待闸时间的分布函数［24］，有

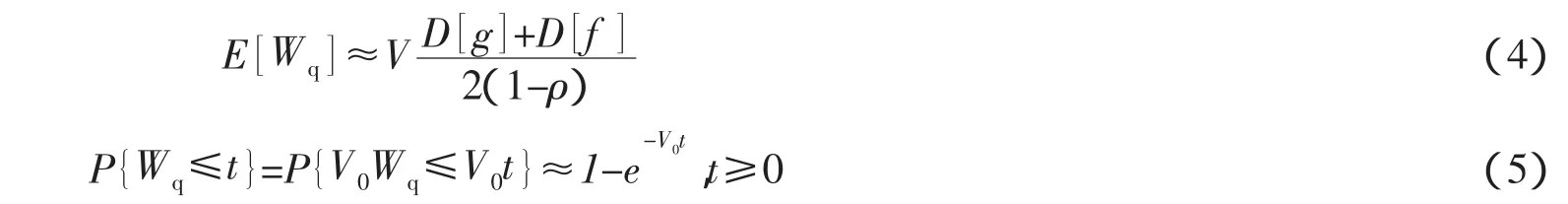
式中：E［Wq］为船舶的平均待闸时间；D［g］和D［f］分别为服务时间和到达间隔时间的方差。也就是说，在高负荷状态下，船舶待闸时间的分布近似为负指数分布，均值即为平均待闸时间。由此可以看出，船舶待闸时间的长短不仅与断面船舶流量以及船舶过闸量的大小（交通负荷）有关，还与船舶到闸和过闸的离散程度有关，这与船闸运行管理的实际经验一致。

2.3 结果与验证

表1根据施桥船闸的到闸和过闸船舶小时流量统计了G/G/1排队模型中的V和C（均为船闸系统忙期的均值），由ρ≈1可知，施桥船闸在忙期处于高负荷状态，可采用式（4）近似求解船舶的平均待闸时间，结果列于表1，其中Wq为模型计算结果，Wo为实际统计结果。同时以2004年全部待闸船舶的待闸时间分布为例，按式（5）给出了其理论分布见图2（实际分布见图1）。

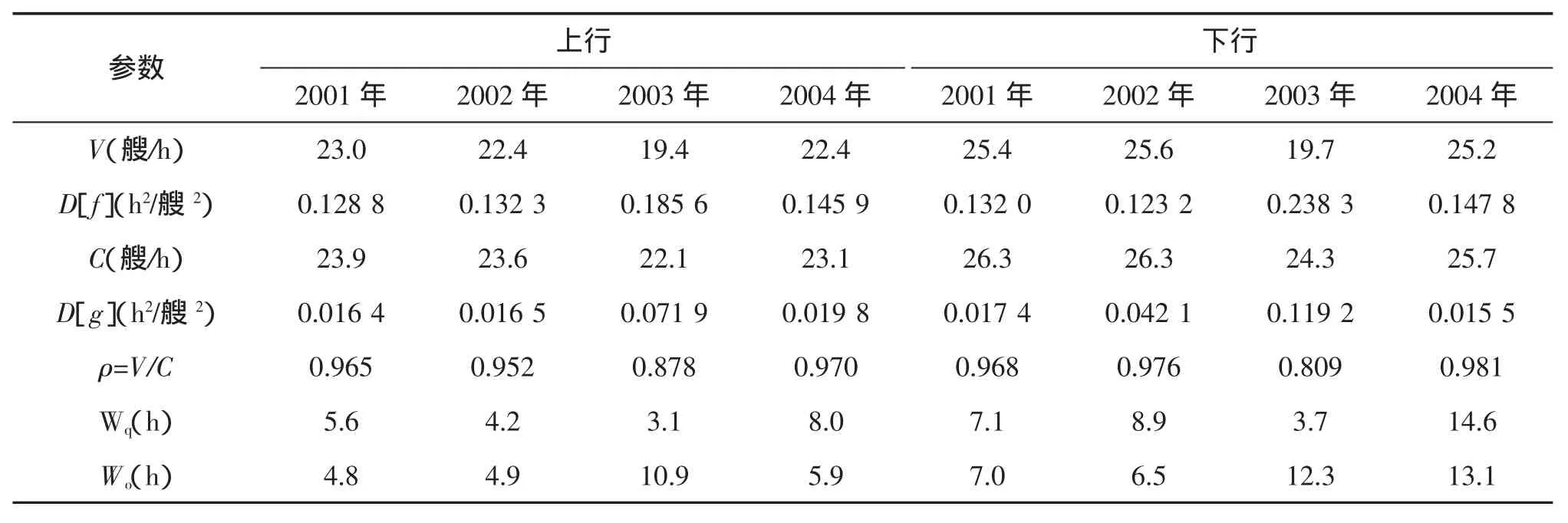
表1 施桥船闸船舶待闸时间计算参数与结果验证Tab.1 Calculation and validation of approximate delays at Shiqiao lock

从计算结果可以看出，尽管采用了诸多假设和近似条件，G/G/1排队模型仍能合理地给出船舶的平均待闸时间，而且船舶待闸时间的理论分布与实测数据点吻合程度良好。2003年存在较大偏差是由于船闸7月份停航，而该模型不能对此进行合理模拟而造成的。因此G/G/1排队模型及其近似解能够用来估算施桥船闸正常运行时的船舶待闸时间，也可应用于类似繁忙船闸的船舶待闸时间研究。

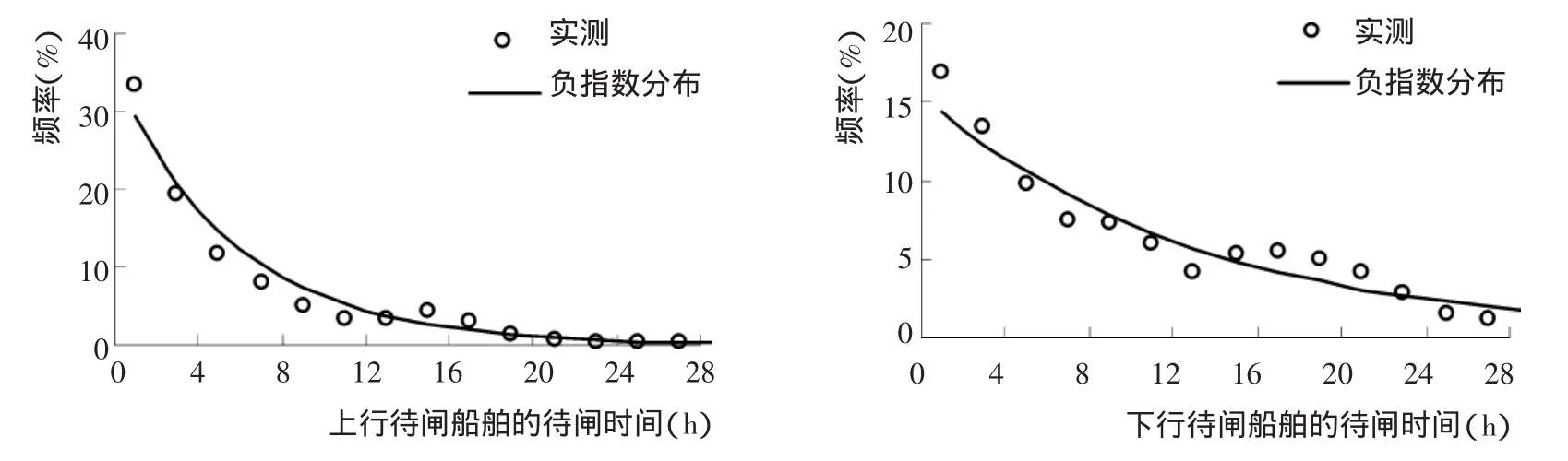
图2 施桥船闸2004年船舶待闸时间的理论分布Fig.2 Theoretical distribution of delays at Shiqiao lock in 2004

3 一次过闸平均载重吨位

影响船闸通过能力的因素非常多，其中一次过闸平均吨位集中反映了过闸船舶的类型和组成及其过闸特点等，是船闸通过能力计算中的关键内容。《规范》推荐通过对不同设计船型、船队进行组合来确定一次过闸平均吨位。由于该方法需要确定设计船型及其组合这2个耦合因素，是目前船闸通过能力计算中的难点。为回避过闸设计船型的选取及其组合等不确定性因素，下面根据船闸和船舶的交通特性，基于过闸船舶的吨位与面积关系［5］，研究一次过闸平均吨位的计算模型，为船闸通过能力的计算提供新思路。

3.1 模型的建立

船舶是籍水浮力随船闸闸室内水体的升降来克服航道上下游的集中水位差，也就是说，船舶过闸需要的是闸室内的水域面积（假定水深条件满足），闸室内水域面积越大，所能容纳的船舶面积就越多，一次过闸平均吨位就越大。由此可以看出，尽管一次过闸平均吨位的确定涉及到许多复杂的动态因素，但关键还是闸室的有效面积和过闸船舶的面积。因此，根据船闸闸室有效面积内的船舶面积，再通过船舶吨位与面积之间的关系，得到一次过闸平均载重吨位G计算模型

式中：ga为过闸船舶的平均吨位；λ为闸室利用率；S为闸室有效面积；s（ga）为过闸船舶的平均面积，由函数s（g）和ga确定。该模式结构简单，回避了过闸设计船型的选取及其组合等不确定性因素，根据实际或预测的船舶平均吨位即可连续计算一次过闸平均吨位，提高了预测工作的可操作性、可靠性和效率。

3.2 内河船舶的吨位与面积关系

通过分析，内河船舶的吨位与面积关系s（g）是确定的，可采用线性、二次多项式等进行最小二乘回归分析得到，具体分析内容参见文献［5］。表2给出了根据京杭运河标准船型以及京杭运河施桥船闸断面2001～2004年每年7月的实际船舶资料分析得到的结果（a1，a2，b1，b2，c2均为回归系数，r为相关系数）。

表2 实际船舶和标准船型的吨位与面积关系的回归系数Tab.2 Regression coefficients for function of the area and tonnage of actual and standard vessels

3.3 闸室利用率λ

理论上，0＜λ＜1，其最大值与闸室有效面积、过闸船舶的尺度和标准化程度有关，其平均值还与船舶到达的统计分布以及船闸的繁忙程度等有关。以京杭运河施桥船闸为例，根据该船闸2001～2005年的一次过闸资料，按不同闸室和航向，计算了总计超过13万个闸次的闸室利用率。为便于统计分析，将闸室利用率按间距0.1分成10个等级，统计每个等级所出现的闸次数，计算其对应的比例，绘出闸室利用率的分布图。图3给出了一线上行和二线下行的统计分析结果。总体上闸室利用率近似正态分布，尽管随时间有右偏趋势，但仍比较稳定，多年平均值为0.55，表明闸室利用率的统计量是个比较稳定的参量。此外还收集了葛洲坝和三峡船闸的年平均闸室利用率（表3和表4），可以看出，这2个船闸的闸室利用率也比较稳定，其值在0.52～0.78，多年平均值分别为0.58和0.74，与施桥船闸的统计结果非常接近。

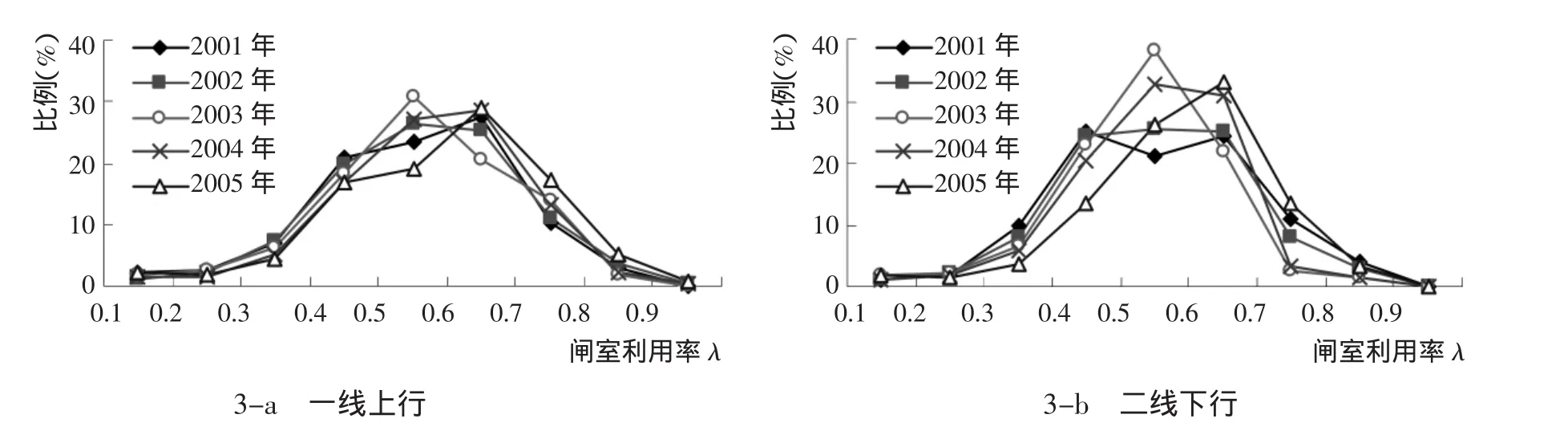
图3 京杭运河施桥船闸的闸室利用率分布Fig.3 Distribution of the percent of available chamber at Shiqiao lock

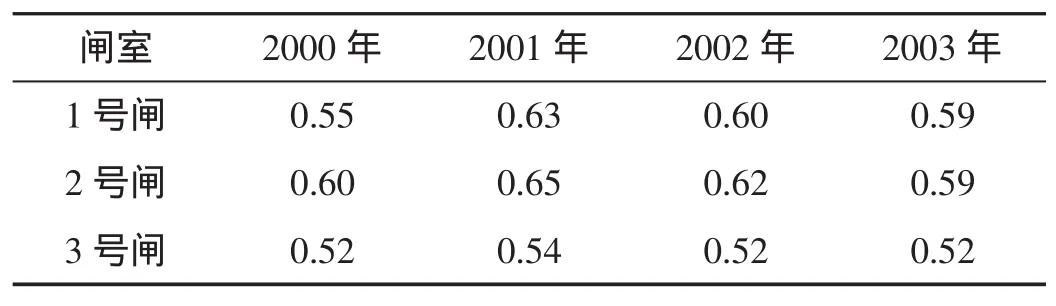
表3 葛洲坝船闸闸室利用率平均值Tab.3 Averaged values of the percent of available chamber at Gezhouba lock

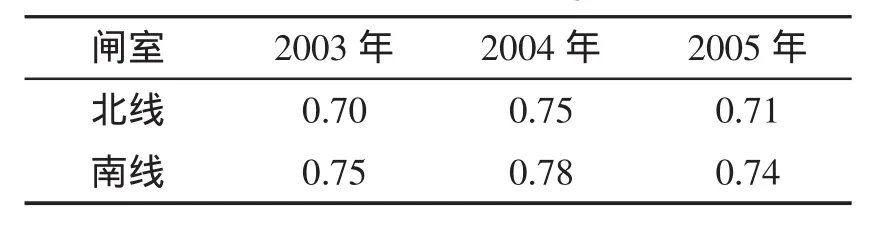
表4 三峡船闸闸室利用率平均值Tab.4 Averaged values of the percent of available chamber at the Three Gorges lock

3.4 实例验证

以京杭运河施桥船闸一线上行和二线下行为例，采用式（6）计算一次过闸平均吨位（表5）。表5中，λ为统计的年平均值；ga为统计的过闸船舶的平均吨位；m为统计的实际一次过闸平均艘数；G0为统计得到的实际一次过闸平均吨位；G2p和G1p分别为采用各自年份实际抽样船舶的吨位与面积的二次多项式和线性关系（回归系数见表2）计算的一次过闸平均吨位（其中2005年实际船舶的s（g）借用2004年值）；G2d、G1d分别为采用表2中京杭运河标准船型吨位与面积的二次多项式、线性关系计算的一次过闸平均吨位；r2p、r1p、r2d、r1d分别对应 G2p、G1p、G2d、G1d与 G0的相对误差。

总体上计算的一次过闸平均吨位值偏小，相对误差主要在10%以内，其（绝对值）平均值为4.8%，而且G1d的相对误差最大仅6.0%，表明该方法合理可行。从各种s（g）计算的结果来看，采用各自年份实际船舶资料得到的一次过闸平均的相对误差总体上与标准船型相当，考虑到往往难以获得大量实际船舶资料，而且其s（g）的回归系数是随着实际船舶的动态发展而变化，应用时宜采用该航道标准船型得到的s（g）。至于采用何种s（g）关系，可根据实际情况具体分析，如无特别要求，可采用形式简单的线性关系。

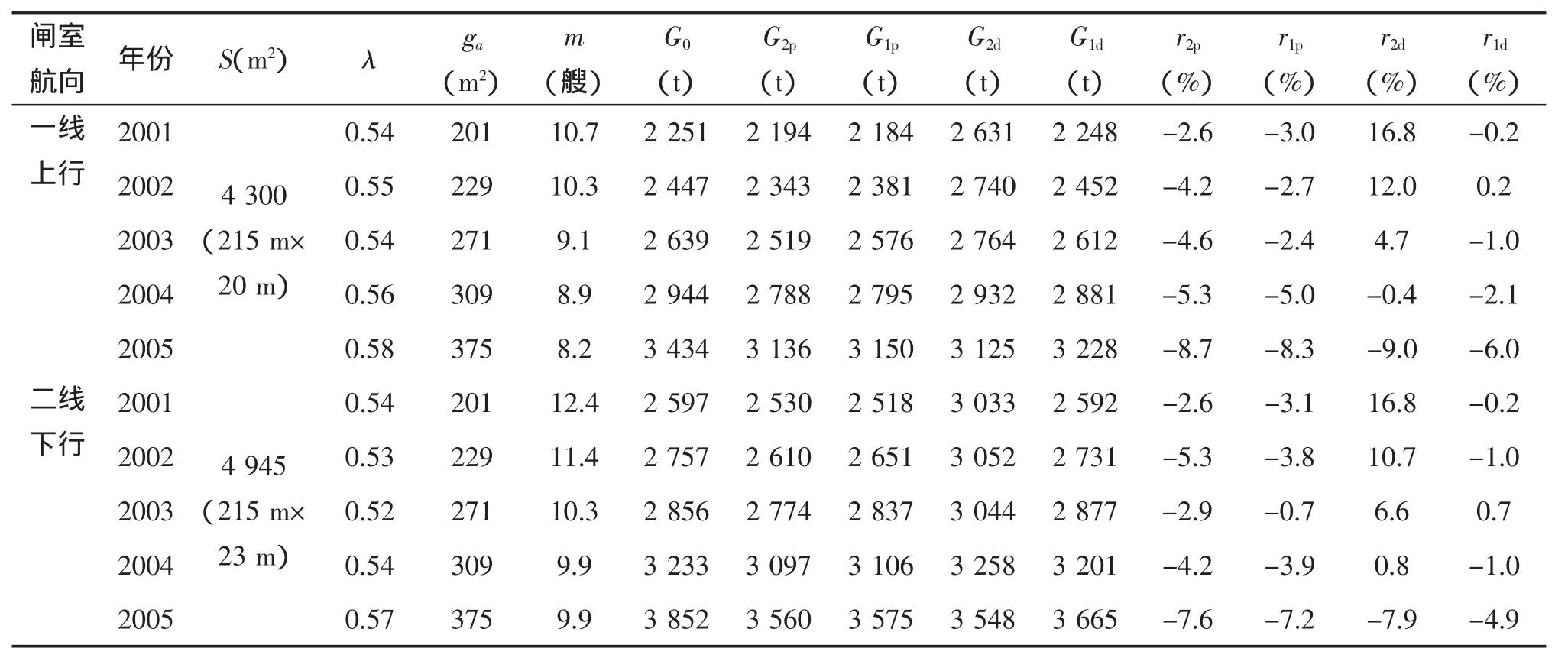
表5 施桥船闸一次过闸平均吨位计算验证表Tab.5 Validation of average tonnage for one lockage at Shiqiao lock

4 船闸服务质量的评价

船闸通过能力不仅是船闸通过船舶数量的表达，还应是船舶通过船闸质量的描述。船闸的通过能力分析不仅要计算船闸通过船舶的数量，也要评价船舶通过船闸的服务质量感受（如过闸时的延误、船员感受等）。或者说既要充分考虑船闸工程的效益，也要兼顾过闸船舶的效益，只有这样，才能全面反映船闸的实际运行情况，船闸工程的综合效益才能达到最优，就如港口规划中，使港方和船方总费用最小的码头最优泊位数和泊位利用率［26］。基于此，廖鹏［2］和张玮等［27］据京杭运河施桥船闸、三峡船闸等船闸的运行资料，通过对内河船舶交通（流）特性的分析，引入船闸服务水平概念，从船闸通航基础设施的角度来评价反映船闸的服务或运行质量，初步阐述了船闸服务水平的定义、划分标准、评价指标及其计算方法、工程应用等，建立了基于服务质量的船闸通过能力研究新方法。限于资料和认识水平，在服务质量的等级划分中尚未考虑船员的感受。

另一方面，在道路通行能力研究中，一直非常重视道路使用者从道路状况、交通条件、道路环境等方面可能得到的服务程度或服务质量，如可提供行驶速度、舒适、方便以及经济安全等方面所达到的实际效果，并采用服务水平指标来衡量交通设施的运行状况以及使用者对设施运行质量的感受，量化道路的综合服务质量。例如，高速公路基本路段的服务水平主要以道路上的车辆运行速度和交通量与可能通行能力之比来综合反映［28］。信号交叉口道路的服务水平评价，近年来更加强调驾驶员的感受，通过建立影响驾驶员对服务水平感受的指标体系，利用回归模型或综合评价方法，预测驾驶员对信号交叉口服务水平的感受的量化值［29］。相比之下，目前关于船闸通过能力研究的已有成果，在研究的理念、理论基础和研究内容上均存在较大的差距，需要依托丰富的船闸运行基础数据，深入分析内河船舶交通（流）的特性，改进现有船闸通过能力（过闸船舶总吨位和货运量）的计算方法，分析并建立过闸船舶的延误模型，预测船员对船闸服务质量感受的量化值，在此基础上构建船闸服务质量的指标和评价体系，建立基于服务质量的船闸通过能力分析新方法，以及船闸运行服务质量的评价模型。

5 结语

随着内河水运在综合运输体系中日益受到重视，在京杭运河、长江上游、西江航运干线等航道上，越来越多的大型现代化船闸即将建设并投入使用，如果对交通规划、设计与评价缺乏科学合理的指导，这些大型永久设施将为我国内河水运的可持续发展埋下隐患。因此有必要及时建立船闸通过能力分析的新方法，以期对现有的计算方法进行改进、补充和完善，更加科学合理地指导船闸的规划、设计与调度管理，从而推动内河水运交通规划与管理的理论研究。需要强调的是，内河航道和船闸的交通问题具有很强的实践性，需要基于大量的系统完整的观测数据和资料开展工作，内河航道船舶流和船闸运行数据和资料的收集和整理是一项非常重要的基础性工作，而这恰恰是目前国内比较薄弱的环节，需要引起各方的重视。

［1］廖鹏.内河船闸通过能力研究进展［J］.水利水运工程学报，2009（3）：34-40.LIAO P.Review on research of lock capacity at inland waterway locks［J］.Hydro-Science and Engineering，2009（3）：34-40.

［2］廖鹏.船闸通过能力研究［D］.南京：河海大学，2007.

［3］廖鹏.繁忙船闸的船舶待闸时间分析与估算［J］.东南大学学报，2009，39（2）：408-412.LIAO P.Estimation and analysis on delays at busy waterway lock［J］.Journal of Southeast University，2009，39（2）：408-412.

［4］廖鹏，张玮.船闸一次过闸平均吨位计算模型［J］.东南大学学报，2010，40（1）：207-212.LIAO P，ZHANG W.Analytical model for average lockage tonnage of waterway lock［J］.Journal of Southeast University，2010，40（1）：207-212.

［5］廖鹏，张玮.内河运输船舶的吨位与面积关系研究［J］.武汉理工大学学报：交通科学与工程版，2009，33（4）：639-642.LIAO P，ZHANG W.Research on relationship between the tonnage and area of inland vessels［J］.Journal of Wuhan University of Technology：Transportation Science&Engineering，2009，33（4）：639-642.

［6］米哈依洛夫 A B.船闸［M］.上海：科学技术出版社，1957.

［7］Bottoms E E.渠化水道的实际通过能力［J］.水运工程专题情报，1974（3）：1-9.Bottoms E E.Practical channel capacity［J］.Special Information of Port and Waterway Engineering，1974（3）：1-9.

［8］DeSalvo J S，Lave L B.An analysis of towboat delay［J］.Journal of Transportation Economy Policy，1968，2：232-241.

［9］Wilson H G.On the application of queuing theory to lock capacity analysis［J］.Transportation Research，1978，12（3）：176-180.

［10］Dai M D M，Schonfeld P.Metamodels for estimating waterway delays through series of queues［J］.Transportation Research：Part B，1998，32（1）：1-19.

［11］Martinelli D，Schonfeld P.Approximating delays at interdependent locks［J］.Journal of Waterway，Port，Coastal and Ocean Engineering，1995，121：300-307.

［12］Ting C J，Schonfeld P.Control alternatives at a waterway lock［J］.Journal of Waterway，Port，Coastal and Ocean Engineering，2001，127：89-96.

［13］Jong J C，Schonfeld P.Genetic algorithm for selecting and scheduling interdependent projects［J］.Journal of Waterway，Port，Coastal and Ocean Engineering，2001，127：45-52.

［14］Wang S L，Schonfeld P.Scheduling interdependent waterway projects through simulation and genetic optimization［J］.Journal of Waterway，Port，Coastal and Ocean Engineering，2005，131：89-97.

［15］Wang S L，Schonfeld P.Demand elasticity and benefit measurement in a waterway simulation model［J］.Transportation Research Record，2007，2 033：53-61.

［16］National Research Council.Review of the U.S.Army Corps of Engineers restructured Upper Mississippi river-Illinois Waterway feasibility study［R］.Washington：The National Academics Press，2004：1-80.

［17］JTJ305-2001，船闸总体设计规范［S］.

［18］闵朝斌.水资源综合利用与航运现代化［M］.北京：中国水利水电出版社，2005.

［19］张玮，廖鹏，梁应辰，等.船闸通过能力计算中的若干问题研究［J］.武汉理工大学学报：交通科学与工程版，2005，29（5）：681-684.ZHANG W，LIAO P，LIANG Y C，et al.Discussion on the calculation of lock capacity［J］.Journal of Wuhan University of Technology：Transportation Science and Engineering，2005，29（5）：681-684.

［20］肖恒辉，齐欢，王小平，等.船舶调度闸外编排算法［J］.交通运输工程学报，2007，7（1）：26-29.XIAO H H，QI H，WANG X P，et al.Arrangement algorithm outside ship lock during ship scheduling［J］.Journal of Traffic and Transportation Engineering，2007，7（1）：26-29.

［21］ZHANG X P，YUAN X H，YUAN Y B.Improved hybrid simulated annealing algorithm for naviagation scheduling for the two dams of the Three Gorges Project［J］.Computers and Mathematics with Applications，2008，56：151-159.

［22］丰玮，吴凤平，张玉韬.闸室船舶组合优化动态模型［J］.河海大学学报：自然科学版，2006，34（6）：697-700.FENG W，WU F P，ZHANG Y T.Dynamic optimization model for ship combination in lock chambers［J］.Journal of Hohai U-niversity：Natural Sciences，2006，34（6）：697-700.

［23］Gartner N H，Messer C J，Rathi M.Revised monograph on traffic flow theory［R］.Washington，D.C.：Federal Highway Administration，1996.

［24］唐应辉，唐小我.排队论：基础与分析技术［M］.北京：科学出版社，2006.

［25］Kleinrock L.Queueing systems volume I：Theory［M］.New York：John Wiley&Sons Inc，1975.

［26］洪承礼.港口规划与布置：2版［M］.北京：人民交通出版社，1999.

［27］张玮，廖鹏，陶桂兰，等.船闸服务水平概念的引入及其确定方法［J］.中国港湾建设，2004（1）：10-14.ZHANG W，LIAO P，TAO G L，et al.Study on level of service at a waterway lock［J］.China Harbour Engineering，2004（1）：10-14.

［28］Transportation Research Board.Highway Capacity Manual，4th ed［M］.Washington，D.C.：National Research Council，2000.

［29］Wang X S，Abdel-Aty M，Almonte A M，et al.Incorporating traffic operation measures in safety analysis at signalized intersections［J］.Transportation Research Record，2009，2 013：98-107.