船闸闸首非线性有限元计算分析

杨 斌，朱 旭

（1.重庆交通大学 河海学院，重庆400074；2.广州港工程设计所，广州 510700）

闸首是船闸的关键部位，闸首结构的安全稳定是整个船闸正常工作的保证［1］。闸首由两侧边墩和底板构成，设有闸门、阀门及启闭机械。布置在闸首的设备较多，轮廓形状不规则，且受力状态十分复杂，承受的荷载既有垂直于船闸纵轴线方向的横向荷载和竖向荷载，又有平行于船闸纵轴线方向的纵向荷载，还有由闸门传来的巨大集中力。纵向荷载和竖向荷载沿船闸纵轴线方向变化较大，横向荷载沿船闸纵轴线方向也有变化［2］。因此闸首结构是一个典型的空间受力结构。

许多学者采用不同的手段和方法对闸首结构进行了研究。河海大学的冯大江［3］将结构、土体与结构接触面看成一个系统中相互作用的3个方面，采用Duncan等提出的土的非线性本构模型和Desai接触面单元，应用Biot固结理论，结合考察施工宽缝封合前后，地基固结时间效应，结构物浇筑、边墩墙后回填土填筑，地下水位控制的相互作用与影响，对结构施工进度及加载过程进行模拟，得到了与原型观测较为接近的结果。2003年周清华［4］结合Biot固结理论和Duncan&Zhang双曲线本构模型，既考虑土体材料的非线性，又考虑变形协调条件对固结过程的总应力的影响，研究了墩底分浇式船闸闸首底板的算法，实测数据验证表明，应用Biot固结理论法能较好地反映地基与结构共同工作过程中的力学特性。冯夏庭、张治强和盛谦等［5］设计三峡第三闸首结构时，根据闸首结构受力特点，采用了合理的计算假定和计算方法，对结构进行整体稳定验算和应力、变形及锚杆受力计算。经计算分析，闸首结构在各设计工况下，均能靠结构自重满足整体抗滑稳定和抗倾稳定要求。汪基伟［6］通过对船闸裂缝成因及加固措施的研究，找出了裂缝产生的主要原因，并提出相应的预防措施。周作茂［7］在株洲航电枢纽船闸上下闸首设计中，模拟了软弱岩石地基对闸首不均匀沉降的作用，找到了闸首裂缝产生的原因，并提出了相应的预防措施和对策。重庆交通大学的吕洪根［8］根据规范设计的底板计算结果与原型观测结果、三维有限元计算结果进行对比，认为按规范的设计方法，底板强度计算结果在门前段偏小，即规范的设计方法对底板负弯矩值估计不足，也无法考虑局部应力集中现象，可能对船闸底板受力带来不利影响。

尽管有些学者对船闸闸首结构的受力情况进行了一些研究，但是并没有充分考虑土体的非线性、闸首结构物与土体的相互作用以及闸首结构物在各种水位作用下的受力变形分析。本文采用ANSYS10.0通用计算软件，建立三维非线性弹塑性有限元模型，采用D-P准则进行闸首结构计算，求解闸首结构的应力及变形分布规律。

1 非线性有限元方法

1.1 基本理论

随着科学技术的发展，线性理论已经远远不能满足工程设计的要求，工程问题的求解己经由线性问题求解发展到非线性问题分析。如岩石、土壤、混凝土等，仅靠线性计算理论已经不足以解决遇到的问题。有限元解决非线性问题的基本思路就是用一系列线性问题的解来逐步逼近非线性问题的解，非线性问题的解可以理解为一系列线性解的迭代结果。

近似的非线性求解是将载荷分成一系列的载荷增量。可以在几个荷载步内或者在一个荷载步的几个子步内施加荷载增量。每一个增量求解完成后，继续进行下一个荷载。增量之前，程序调整刚度矩阵来反映结构刚度的非线性变化［9］。

处理材料非线性问题，不需要重新列出整个问题的表达形式，只要将材料本构关系线性化，就可将线性问题的表达形式推广用于非线性分析。一般来说，通过试探和迭代过程求解一系列线性问题，若在最后阶段，材料的状态参数被调整得满足材料的非线性本构关系，则最终得到问题的解答。而非线性问题的有限元形式都涉及求解非线性代数方程组。

Newton-Raphson方法是求解非线性方程组（1）的一个著名方法，简称Newton法

设 ψ（δ）为具有一阶导数的连续函数，δ=δi是式（1）的第 i次近似解。若

式（1）的近似解为

将式（3）代入式（1），并在 δ=δi附近按一阶 Tayor级数展开，则 ψ（δ）在 δi处的线性近似公式为

Newton法的收敛性较好，但对于某些非线性问题，如理想塑性和塑性软化问题，在迭代过程中KT可能是奇异或病态的，于是KT的求逆就会出现困难。为此可引入一个阻尼因子η，使矩阵或成为非奇异，或使其病态减弱［10］。

1.2 本构模型选取

岩石、土体属于弹塑性材料，弹塑性材料的一个显著特点是应力超过屈服点后，应力应变关系呈非线性，且加载与卸载的应力路径不一样。鉴于摩尔-库仑准则在计算上收敛的困难性，弹塑性有限元程序中大都采用德鲁克-普拉格准则［11］。

地基土材料和回填土均考虑成Drucker-Prager屈服准则的弹塑性材料，Drucker-Prager屈服准则为

式中：a和k分别为岩土体材料粘结力c和内摩擦力Ф的相关系数；I1为应力张量第一不变数；J2为应力偏张量第二不变数。

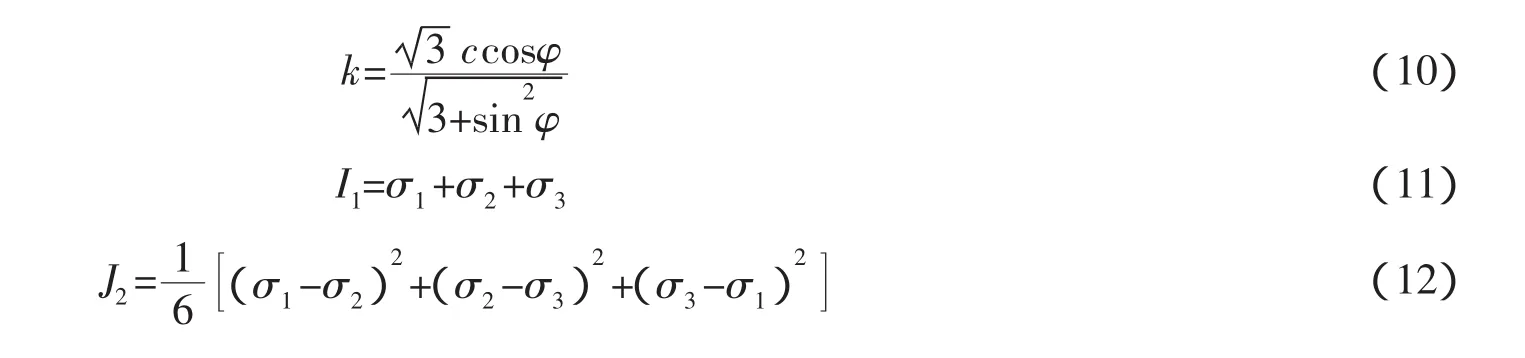
2 算例及分析

本次计算以嘉陵江新政船闸闸首为基本计算结构。该船闸闸首边墩高18.7 m，宽12 m，长14 m，2个边墩之间的距离为16 m，左右边墩对称布置；底板布置在2个边墩之下，厚度为5.1 m。该船闸修建在砂质粘土岩地基之上，左侧边墩后有回填土体。工程材料详细参数见表1。

表1 材料参数Tab.1 Parameters of material

2.1 模型建立

用ANSYS有限元软件建立船闸闸首结构模型［12］。由于闸首底板排水廊道采用C30聚丙烯纤维砼加固，在进行有限元整体分析时，考虑底板是一个整体。选取上闸首底板以下35 m作为地基，根据设计，边墩后部回填土长度约为35.1 m。模型采用笛卡尔直角坐标系，Z轴与船闸纵轴线一致，指向下游为正；沿铅垂向为Y轴，向上为正；X轴以右手法则确定；坐标原点位于地基的左下角靠近上游的顶点。由于闸首结构物的边墩在长度和宽度方向上都较大，且有较大的刚度，为了分析出闸首在较不安全情况下的受力特征，假设闸室墙没有与闸首墩相互作用，选取图1所示的实体模型。

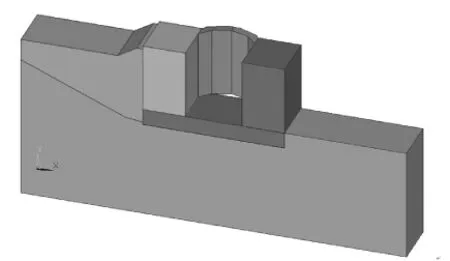
图1 船闸闸首模型图Fig.1 Model of lock head

2.2 网格划分

由于模型中基础和回填土的几何尺度比较大，采用自由网格划分技术，单元形状采用四面体Tet单元；闸首底板、边墩和闸门几何尺寸较复杂，也采用四面体Tet单元。在各部分连接区域采用相同的网格尺寸，以使连接处的分界网格节点能够很好的对应（节点坐标相同）。本模型中共划分了81 270个单元，65 727个节点。计算网格模型见图2。

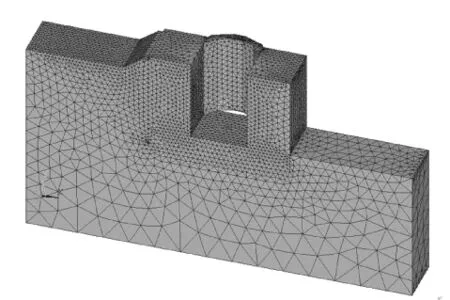
图2 船闸闸首网格图Fig.2 Mesh of lock head

2.3 载入和求解

对船闸闸首结构进行线性弹性计算，地基和回填土体采用弹塑性D-P本构模型进行非线性计算。为了更好地模拟工程的实际受力情况，须进行分步加载。首先对地基结构施加重力。模型建立后，为了使地基上的建筑物和回填土荷载在地基施加重力场后再载入在地基上，采用ANSYS杀死单元技术，杀死建筑物、回填土和闸门的所有单元。为了能顺利杀死建筑物和回填土单元，需要把ANSYS的大变形和线性搜索打开，设置好时间步，选用Full N-R求解。采用同样的方法对模型依次施加上闸首结构物荷载、回填土荷载和闸门上的水压力等荷载。

2.4 计算成果及分析

2.4.1 完建工况分析

在完建工况下，闸门上不受水压力，但左侧的边墩受到较大的回填土荷载作用。

（1）位移结果。

计算结果表明，完建工况下在Y方向上整个闸首建筑物和回填土都向下沉陷。最大沉降位移发生在回填土的中部，达到最大值8.1 cm。结合前面只有地基土体荷载的情况进行对比分析发现，在回填土体和闸首结构物自身的重力作用下，地基的位移云图在接近结构物的地方有较大的变化，离闸首结构物和回填土体较远的右侧土体受影响相对较小。在同一个边墩上，墩顶的沉降大于墩底，并且从墩底到墩顶逐渐增加，左侧边墩位移大于右侧边墩。X方向左侧边墩由于受到回填土荷载作用，在土压力作用下产生较大位移，而右侧的边墩支持墙，由于没有回填土压力的直接作用，位移相对较小，闸首底板受到各方面的约束，在X方向的位移很小。没有闸门水压力的推力作用下，整个结构物在Z方向（船闸纵轴线方向）上的变形很小。图3为完建工况的位移云图。

（2）应力结果。

计算结果表明，在回填土和闸首结构物重力作用下，在闸首底板中间的上部产生拉应力。第一主应力的最大拉应力为0.68 MPa，第三主应力的最大拉应力为0.13 MPa。由于闸首底板采用C25钢筋混凝土材料，所产生的拉应力没有超过材料强度。第一主应力产生的最大压应力在地基土体的左下角底部，为0.5 MPa，第三主应力产生的最大压应力在回填土和闸首底板相交的部位，最大值为2.9 MPa；边墩对地基应力的影响在边墩一半高度左右。离闸首结构较远的位置，地基应力受影响明显较小，且呈均匀分布。图4为模型的vos Mises应力云图。

2.4.2 运用高水工况分析

选取上游最高通航水位和下游最低通航水位组合。闸首门坎高程为306.1 m，闸首顶高程为325.6 m，上游最高通航水位为324 m，下游最低通航水位为309.9 m。在闸门、边墩内侧和闸首底部上均作用有水压力，同时上、下游水位差会对闸首底板产生扬压力等。上述荷载在ANSYS中均采用梯度加载法，分别加载在底板上下两面、支持墙内侧及闸门上。

（1）位移结果。

运用高水工况下，闸首主要承担来自闸门的水压力作用，水压力通过闸门的支枕垫传递给边墩，分解为向下游的推力和向内侧的推力；闸首结构物由于边墩刚度较大，回填土和地基受到闸门推力产生的在Z方向的位移很小，主要发生在闸门上。但对比完建工况下Z方向上的位移结果可以看出，在水压力和底板上扬压力作用下，闸门在Z方向上的位移远大于完建工况。右侧边墩没有受到土体的约束作用，在Z方向上产生的位移大于左侧边墩。最大位移产生在右侧边墩内侧，为0.184 cm。图5为运用高水工况的位移云图。

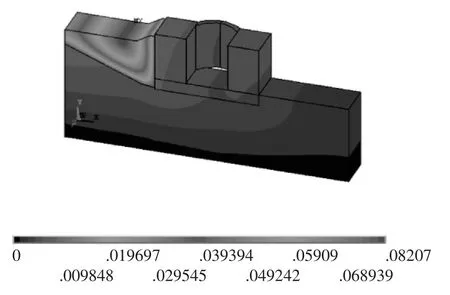
图3 完建工况总位移云图Fig.3 Total displacement contour under construction completion condition

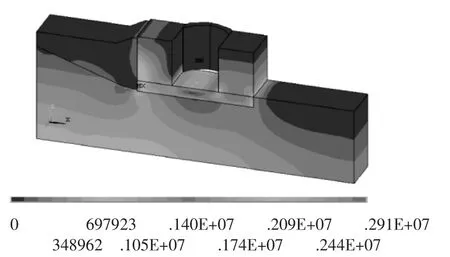
图4 完建工况vos Mises应力云图Fig.4 Stress contour under construction completion condition for vos Mises

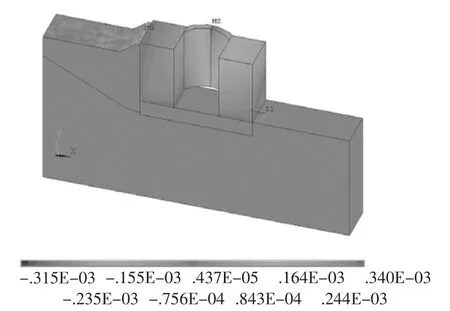
图5 正常运用高水位Z方向应变云图Fig.5 Strain contour of normal use of the high water level in Z direction

（2）应力结果。

正常运用高水位工况下，模型的应力计算结果表明，由于水压力和底板上的扬压力的出现，第一主应力最大拉应力出现在闸门上，约为5.6 MPa；第一主应力最大压应力出现在地基体的左下角，约为0.81 MPa。第三主应力最大压应力出现在闸门底端靠近边墩的顶部，约为7.2 MPa；第三主应力最大拉应力出现在闸首底板表面，约为0.21 MPa。地基应力值向上逐渐递减，地基表层应力值最小，出现了很小的拉应力。在闸首底板的边界部位均出现应力集中。图6为模型的vos Mises应力云图。

2.4.3 计算结果验证

选取船闸闸首在完建工况和正常运用高水工况下的外边墩前趾进行应力有限元计算和解析法计算对比分析。

在完建工况下，边墩前趾最大应力值解析法计算为0.953 MPa，有限元计算结果为0.951 MPa，计算结果表明，完建工况的解析法和有限元计算结果相差较小，主要是由于在完建工况下，边墩没有受到闸门水压力的作用，回填土荷载也主要作用在左侧的边墩上，左侧边墩刚度较大，回填土荷载对右侧边墩的作用影响较小，解析法计算时所简化的条件较少，因此2种方法的计算结果较为接近。在高水位工况下，边墩前趾最大应力值解析法计算为1.046 MPa，有限元的计算结果为1.342 MPa，计算结果表明，在正常运用高水工况下，由于闸门上有较大的水压力作用在边墩上，考虑到解析法计算中运用了许多假设条件，必然会对计算结果产生一定的影响。

鉴于有限元方法是根据现实对象的实际结构建立三维实体几何模型，将三维实体模型离散化，并将结构体所受实际载荷分别作用于各单元体上，最后求出各单元体节点力和位移。因此有限元法计算结果能够较真实地反映结构物的实际受力情况。

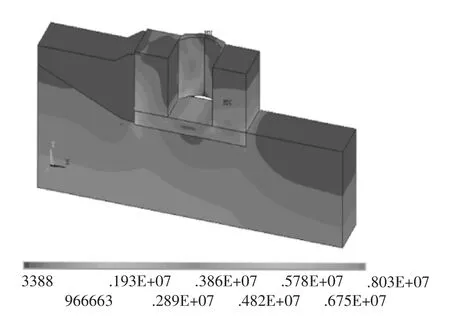
图6 正常运用高水位vos Mises应力云图Fig.6 Stress contour of normal use of the high water level for vos Mises

3 结语

（1）作用于船闸闸首结构上的地基和回填土体是典型的弹塑性材料，考虑工程的实际情况，对其进行非线性结构计算更为合理。

（2）本文运用ANSYS10.0软件，对船闸闸首在完建工况和正常运用高水工况下的应力、应变特征进行三维非线性弹塑性有限元分析。同时结合解析法计算结果，验证了模型的正确性和实用性。

（3）利用有限元计算结果对闸首的计算，工程设计人员可以很清晰地掌握整个船闸结构的变形和应力分布规律，为工程设计和研究提供了依据。

［1］王作高.船闸设计［M］.北京：水利电力出版社，1992.

［2］王丽军.船闸结构内力的分析与研究［D］.合肥：合肥工业大学，2006.

［3］冯大江.应用Biot固结理论的船闸闸首结构非线性有限元分析［D］.南京：河海大学，2005.

［4］周清华，边立明，徐泽中.墩底分浇式船闸闸首底板算法研究［J］.水运工程，2003（1）：43-46.ZHOU Q H，BIAN L M，XU Z Z.A Study on Algorithm for Lock Head Floor of Shiplock of Separately Casted Floor and Piers［J］.Port&Waterway Engineering，2003（1）：43-46.

［5］冯夏庭，张治强，盛谦，等.三峡工程永久船闸三闸首区开挖变形特征的智能分析［J］.岩石力学与工程学报，2001（5）：633-637.FENG X T，ZHANG Z Q，SHENG Q，et al.Intelligent Analysis of Deformation Behaviors of Permanent Shiplock of the Three Gorges Project［J］.Chinese Journal of Rock Mechanics and Engineering，2001（5）：633-637.

［6］汪基伟.船闸裂缝成因及加固措施的研究［J］.水利水电技术，2001（9）：5-9.WANG J W.Study on Cause of Cracking and Improvement Measures of a Lock［J］.Water Resources and Hydropower Engineering，2001（9）：5-9.

［7］周作茂.株洲航电枢纽船闸闸首设计［J］.水运工程，2007（8）：89-92.ZHOU Z M.Lock Head Design of Zhuzhou Navigation Power Junction［J］.Port&Waterway Engineering，2007（8）：89-92.

［8］吕洪根.坞式闸首底板计算方法的分析［J］.重庆交通学院学报，1989，28（1）：81-89.LU H G.Analysis of Calculating Method to Lock-Head Floor of Dock Mode［J］.Journal of Chongqing Jiaotong University，1989，28（1）：81-89.

［9］郑颖人，沈珠江，龚晓南.广义塑性力学—岩土塑性力学原理［M］.北京：建筑工业出版社，2002.

［10］王靖涛.建立岩土本构模型的数值方法［J］.华中科技大学学报：城市科学版，2002，19（1）：44-47.WANG J T.Numerical Method in Modeling the Constitutive Relations of Rock and Soil［J］.Journal of Huazhong University of Science and Technology：Urban Science Edition，2002，19（1）：44-47.

［11］赵尚毅，郑颖人，刘明维，等.基于Drucker-Prager准则的边坡安全报系数定义奇迹转换［J］.岩石力学与工程学报，2006，25（1）：2 730-2 734.ZHAO S Y，ZHENG Y R，LIU M W，et al.Definition and Transformation of Slope Safety Factor Based on Drucker-prager Criterion［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25（1）：2 730-2 734.

［12］王国强.实用工程数值模拟技术及其在ANSYS上的实践［M］.西安：西北工业大学出版社，1999.