基于人工神经网络的胶州湾浮游植物生物量模拟

石洪华 ，方国洪 ，孙玉茗 ，郑 伟 ，胡 龙

（1.国家海洋局第一海洋研究所，青岛266061；2.中国科学院海洋研究所，青岛266071；3.中国海洋大学 数学科学学院，青岛266100；4.复旦大学 数学科学学院，上海200433）

在生物与环境关系的研究中，基于数学模型的统计和趋势预测方法已得到了成功应用。这些方法在不同预测中体现出各自的优势，因其给出了具体的函数关系，意味着将系统演变规律化、公式化。然而海湾生态系统的演变具有复杂的动力学机制，因此该类方法限制了预测的准确性。海湾生态系统变化的驱动因素非常复杂，目前还难以找到合适的表征海洋生物变化的环境因子或组合，其相关研究仍在进一步探索之中。

人工神经网络的预测方法建立在对输入和输出变量的非线性映射之上，只和训练样本及目标有关。该方法不仅克服了具体函数表达式的局限性，还能通过学习、训练过程，选择相对最优网络对目标值进行预测。BP网络是典型的前向型网络，在网络结构和学习算法上比较成熟，因其强大的并行处理能力和非线性映射技术，在很多领域有很好的应用。很多研究者采用前向型网络，模拟了浮游植物藻华发生的时间和量级，预测了其生物量丰度［1-5］。与其他方法相比，神经网络模型在藻类浓度预测方面具有较高的精度，已经成为环境系统模拟的有用工具［3，6］。

本文选择海洋浮游植物生物量的代表性生物因子叶绿素a（Chl a）作为研究对象，做了三方面工作。首先以胶州湾为例，构建BP人工神经网络模型；利用不同站位不同月份的观测资料检验了该模型可靠性；建立了ANN模型参数灵敏度分析模型，分析了各模型输入参数对预测结果的贡献。

1 调查站位与数据

胶州湾位于黄海西部，山东半岛南岸，以团岛头与薛家岛脚子石连线为界，是与黄海相通的半封闭海湾，海湾东西宽27.8 km，南北长33.3 km，海湾面积为387 km2（其中水域面积约320 km2），海湾岸线长187 km，口门宽度3.14 km。近年来，随着青岛市经济持续快速发展、人口不断增加，胶州湾海域水质不断恶化，海域生态系统结构发生了较大改变，生态系统服务功能退化，赤潮等海洋生态灾害频发。

2003年1月～12月，国家海洋局第一海洋研究所在胶州湾进行了连续观测，观测要素包含常规化学指标、生物指标和部分水文指标，共设置9个站位（图1），调查频率为每月一次。本文所用水环境指标包括溶解氧浓度DO、pH值、化学需氧量浓度COD、DIP浓度、DIN浓度、硅酸盐浓度、石油类浓度和海水表层温度，采用表层叶绿素a浓度含量代表浮游植物生物量。

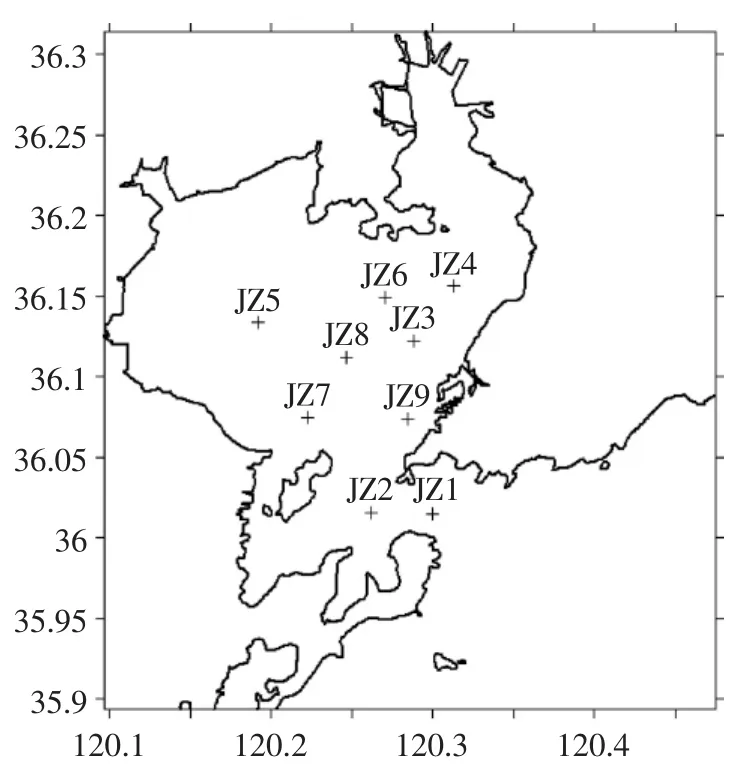
图1 研究区和调查站位Fig.1 Study area and sampling stations

2 BP人工神经网络模型

本文采用多输入单输出的三层网络结构。根据所获数据特点，用8项水环境参数预测生物量的变化。

2.1 数据标准化方法

为保证网络有好的收敛性和映射能力，将数据映射到［0，1］区间内。数据标准化公式

式中：xmax为最大观测值；xmin则为最小观测值；xi为第i个实际观测值；xi′为其标准化变量。

2.2 隐层神经元个数的选择

在BP网络中，隐层节点数不仅对神经网络模型性能影响很大，而且是训练时出现“过拟合”的直接原因，但是目前理论上还没有一种科学的和被广泛接受的确定方法。隐层节点数不仅与输入、输出层的节点数有关，更与问题的复杂程度、转换函数的型式以及样本数据的特性等因素有关。本文在保证一定精度、确保足够高的泛化能力前提下，选取隐层神经元个数的基本原则为：（1）取尽可能紧凑的结构，取尽可能少的隐层节点数；（2）隐藏层神经元个数必须小于训练样本数；（3）训练样本数必须多于网络模型的连接权数（一般为2～10倍）。本文拟选取的隐层神经元个数满足以下公式

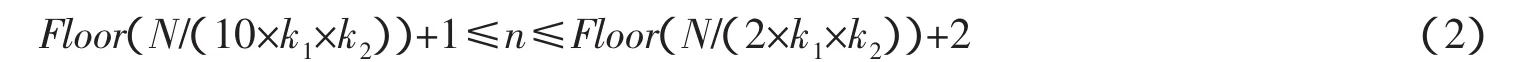
式中：Floor（·）为取下整的函数；n为隐含层神经元个数；N为训练样本数；k1为网络输入层节点数；k2为网络输出层节点数。

对满足式（1）的每一个隐层数分别建立BP神经网络（网络其他参数相同），训练网络后，针对每一个网络对检测集进行模拟得出模拟值，将模拟值与真实值做均方差，最后找出最小的均方差所对应的隐层数作为本试验最优的隐层数进行试验。

2.3 人工神经网络训练

将所获数据分为训练集和检测集2大类，而每一类集合分别包含输入子集和输出子集。其中，检测集样本应独立于训练集，具有代表性，样本选择尽量分散，样本数不低于选练集样本数的10%。设置误差限、学习率、传递函数等，根据上述方法将数据标准化、确定隐神经元个数范围后，对网络进行训练，选择隐层最优神经元个数的网络作为仿真和预测的网络。

2.4 BP人工神经网络检验

为检验BP人工神经网络预测的准确性，将网络输出与检验样本中原始数据进行比较。定义相对误差指标如下

3 胶州湾浮游植物量模拟的BP网络与精度检验

3.1 模型建立

以胶州湾2003年1～12月各站点数据为样本，分为训练集和检测集两大类，而每一类集合各自又分为输入集和输出集2种。从代表性和分散性的角度，选择8套数据构成检验样本（表1）。

表1 检测集站位及预测误差Tab.1 Test set station and prediction error

以周年连续生态环境监测资料作为训练样本。本文应用的BP网络均设计为单一输出型，尝试通过水质参数预测生物量（叶绿素a）的情形。经过反复试验，综合考虑网络的收敛性和误差等因素，选用包含3个隐层神经元的三层网络（BP）作为预测网络。

网络训练次数为50 000次，训练误差限设为0.01，学习率设为0.02。训练完后，将检测集带入到网络中模拟，得到网络模拟值，再将模拟值逆归一化，最终得到模拟值。

3.2 有效性检验

网络训练后，选择检验集对模型有效性进行检验（表1）。在此基础上，绘出检测集各站点观测值与网络预测值对比图（图2）。结果表明，检验样本相对误差最大值出现在6月份的JZ6站，其值为30.04%。网络的平均相对误差为0.84%，平均绝对误差为11.33%，检验样本预测值与观测值的相关系数为89.43%。因此，认为该BP人工神经网路可以满足一般预测的精度要求，可用于预测研究。

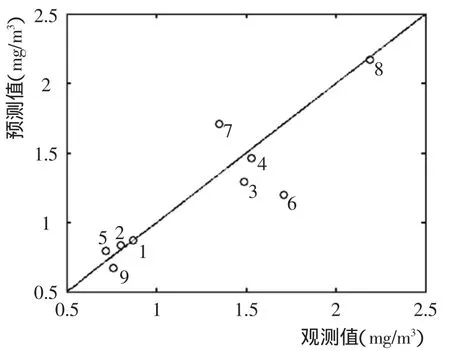
图2 胶州湾Chl a预测值与观测值比较Fig.2 Comparison between the predicted and observed value of Chl a in Jiaozhou Bay

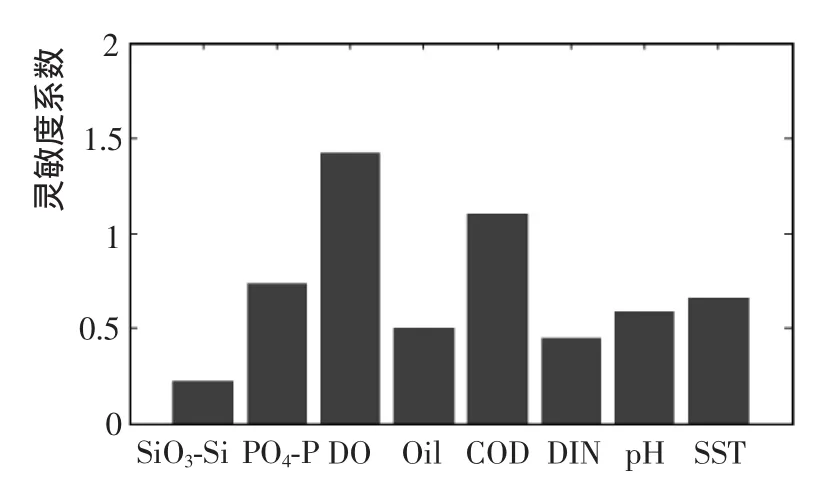
图3 浮游植物生物量对各水环境指标变化响应的平均灵敏度系数Fig.3 Average sensitivity coefficient of the response of phytoplankton biomass to water environment index change

4 网络输出对输入变化的响应

4.1 灵敏度模型及计算方法

网络训练成功后，便可用于预测和仿真。本文为部分揭示所建ANN模型的内部机制，特别是研究网络输出对输入的敏感性，设计了灵敏度指标。该指标定义如下

本文采用网络中训练集作为灵敏度分析的数据来源（这里不用检测集是因为用人工神经网络模拟训练集的结果比模拟检测集的精度要高），每次试验中，每组数据仅有一维变化10%，其他维值不变，然后输入网络仿真，所得值与原来未变化时的值进行比较，最后得到灵敏度变化的矩阵，矩阵的每一列即为每一个因子对叶绿素变化的影响大小。本文所定义的灵敏度可称为全局灵敏度。由于对所有训练样本的输入都作了分析，这些输入样本的分布高度离散，基本代表了不同的初始位置。

4.2 灵敏度分析

对灵敏度矩阵的每一列取平均值，可得到不同环境因子的平均值灵敏度。计算结果表明，浮游植物生物量对各环境要素响应的平均敏感性从大到小为DO＞COD＞PO4-P＞SST＞pH＞Oil＞DIN＞SiO3-Si（图3）。

5 讨论

从以上模型结果可知，BP网络预测可靠性较高，都有较高的拟合度。此例主要是说明应用人工神经网络技术来预测海湾浮游植物生物量，不仅对检验样本有较好的拟合，还可以利用网络优化来提高网络预测性能。更主要的是人工神经网络预测不需要知道预测因子和预测量之间的函数关系，事实上很多关系不是确定的物理关系，只是一种统计意义上的关系。由于BP网络有较强的非线性映射能力，避开了预测因子与预测量的简单确定函数关系。同时又因为网络的黑箱效果，没有把预测因子和预报量的非线性关系限制在固定函数上，在海湾生态系统变化机理尚未完全明确的前提下，该方法提供了一种可行的预测途径。灵敏度分析表明，利用人工神经网络法还可以计算网络输出（浮游植物生物量）对输入（水环境因子）变化的响应。从而在一定程度上揭示了浮游植物变化的动力学机制。本文仅列出全局意义下浮游植物生物量对环境因子变化响应的平均灵敏度系数，不同环境状况下的灵敏度也可同理得出。

致谢：本研究得到丁德文院士和王宗灵研究员的支持和帮助。

［1］Yabunaka K，Hosomi M，Murakami A.Novel application of a back-propagation artificial neural network model formulated to predict algal bloom［J］.Water Science and Technology，1997，36（5）：89-97.

［2］Recknagel F.ANNA—artificial neural network model for predicting species abundance and succession of blue-green algae［J］.Hydrobiologia，1997，349：47-57.

［3］Maier H R，Dandy G C.Neural Network Based Modelling of Environmental Variables：A Systematic Approach［J］.Mathematical and Computer Modelling，2001，33：669-682.

［4］Hou G X，Song L R，Liu J T，et al.Modeling of cyanobacterial blooms in hypereutrophic Lake Dianchi，China［J］.Journal of Freshwater Ecology，2004，19（4）：623-629.

［5］Recknagel F，Kim B，Takamura N，et al.Unravelling and forecasting algal population dynamics in two lakes different in morphometry and eutrophication by neural and evolutionary computation［J］.Ecological Informatics，2006（2）：133-151.

［6］丁德文，石洪华，张学雷，等.近岸海域水质变化机理及生态环境效应［M］.北京：海洋出版社，2009.