基于技术站中转作业的集装箱空箱调配模型

刘 鹏，彭 昕，曲思源

（1.同济大学 交通运输工程学院，上海 201804；2.中鹏实业发展有限公司，广东 广州 510260;3.上海铁路局 调度所, 上海 200071）

传统理，的并铁以路空空车车走调行整距模离型最大小多化将为其目作标为构简建单模的型运获输得问路题网处供需节点间的空车最优分配方案，该模型已在全路技术计划管理信息系统中采用[1]。国内有关运输问题已经取得一些研究成果：有关运输问题的算法将运输问题的启发式算法与传统经典算法进行比较，表明有关运输问题的算法已日趋完善[2]；考虑路网运输能力限制并采取迭代算法进行分步优化，使得模型进一步符合运输实际[3]；通过路网等边界条件的设定使模型具有严密性[4]。然而，传统模型仅考虑空车流在路网上分配的静态效用，只是满足一定约束条件的确定性模型，且忽视空车在技术站的中转作业，不符合运输生产实际，没有技术站参与的空车调配是不完整的。文献[5]研究的技术站空车调整问题仅仅是一个特例[5]，条件是卸车站产生的空车全部在技术站改编后重新分配，路网空车调整的实际情况是既有卸车站发出的空车以专列方式送到装车站，还有部分空车通过小运转或空重混编列车的方式到技术站进行无调中转或改编后重新分配等复杂情况。因此，基于技术站中转作业的集装箱空箱调配模型，将通过对传统模型的研究，借鉴空车调配模型，以集装箱空箱走行里程最少为目标，提出其研究条件和步骤，并结合实例进行分析。

1 建立集装箱空箱调配模型

1.1 前提假设

铁路网是一个封闭的系统结构，在系统内研究集装箱空箱调配问题，节点间不发生空箱对流现象，集装箱卸车站和装车站空箱流供需平衡(对实际不平衡问题采取增设虚拟供需节点的方法构建模型)，集装箱空箱运输过程保持静态稳定。

1.2 构建模型

基于技术站改编作业的集装箱空箱调配问题是扩大化的运输问题。从集装箱卸车站发出的空箱有2 种组织方式：①整列空箱专列以基地直达、阶梯直达、随小运转列车等方式组织空箱整列 (未达到平均编组辆数) 到达集装箱装车站 (以下简称“装车站”)，若经过技术站则为无调中转过程。②部分空箱随空重混编列车方式组织到达相邻技术站集结改编后，由技术站以始发空箱专列或小运转(摘挂列车)方式到达集装箱卸车站 (以下简称“卸车站”)，整个过程需要进行有调中转作业。因此，装车站的空箱到达需要经过卸车站和技术站共同组织，集装箱空箱调配不仅是供需两点间的配空问题，需要研究卸车站对于空箱的装车站直达组织和到达技术站的中转作业组织。

定义路网结构G＝(V，L)，其中，V 为网络中节点的集合；L为边集，即路网所有路段的集合。设V＝(A，C，B)，A、C、B 分别表示卸车站、技术站和装车站的集合，A ＝{a1，a2， …，am}，C ＝{c1，c2，…，cq}，B＝{b1，b2，…，bn}；各路段的容量和流量分别为 Fl和 fl；各技术站改编空箱数和改编能力为 fc和 Fc；ai到 bj距离为 lij；xij为决策变量ai到 bj的空箱数；xi,n+k表示 i 站发出的空箱经由 k 站中转，xm+k,j表示经 k 站中转的空箱到达 j 站。以空箱在路网上走行里程 z 最少为目标建立模型：

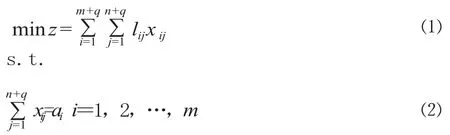
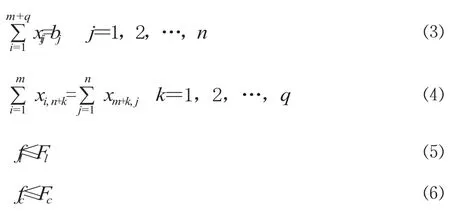
限制条件中，式⑵、式⑶表示供需平衡；式⑷表示技术站出入空箱流平衡；式⑸表示路段运输能力限制；式⑹表示技术站中转作业能力限制。

2 模型求解步骤

第一步：为确保空箱不对流，先规定空箱流方向。一般原则是卸车站与装车站、技术站节点相邻时，由卸车站指向装车站或技术站；两个卸车站或装车站节点相邻时，可先不确定方向，最后检查分配方案后灵活调整。

第二步：按照节点空箱流方向计算卸车站到装车站和技术站间的最短距离。当路网上的节点较多时，可以通过最短路径 ( Dijkstra 或 Flody 等) 算法求得。若存在路权相等的情况可任选其一，求得路网中供需节点间最短路径为初始路径。

第三步：先不考虑路网运输能力限制和技术站中转作业能力限制，当有多个技术站时，为确保运输资源充分利用，规定每个技术站的空箱调整服务范围，综合考虑技术站中转空箱的限制数量和路网通过能力限制，确定带有转运性质的供需空箱流平衡表，据此构建基于技术站中转作业的空箱调整模型。

第四步：利用 LINGO 8.0 软件求解[6]，求得空箱走行距离最小的空箱调整方案。若不能满足需求，则应平衡各技术站间的空箱流，组织某一技术站向另一技术站排空，以求得最终空箱流在路网上的最优分配方案。

3 算例分析

设有 6 个卸车站 (空箱发送量分别是100 TEU、200 TEU、160 TEU、185 TEU、300 TEU、90 TEU)、6 个到达站 (空箱需求量分别为165 TEU、105 TEU、190 TEU、175 TEU、110 TEU、290 TEU)、2 个技术站，空箱总计为 1 035 TEU，节点间的路网结构如图1 所示，图1 中数字为路段长度，km，c1服务范围为a1～a3、b1～b4，改编能力为300 TEU；c2服务范围为a3～a6、b4～b6，改编能力为 400 TEU。其中，a3、a4、b4的空箱配送可以由 2 个技术站共同完成，即技术站可以向相邻技术站配送空箱。

在路网上进行空箱流方向标号 (箭头方向) 如图1 所示，相关运输问题供需平衡表如表1 所示。利用计算机软件经过 16 次迭代求解，可得到空箱走行里程最小 (283 600 km) 的空箱流分配方案如表2 所示。

表1 运输问题供需平衡表 TEU

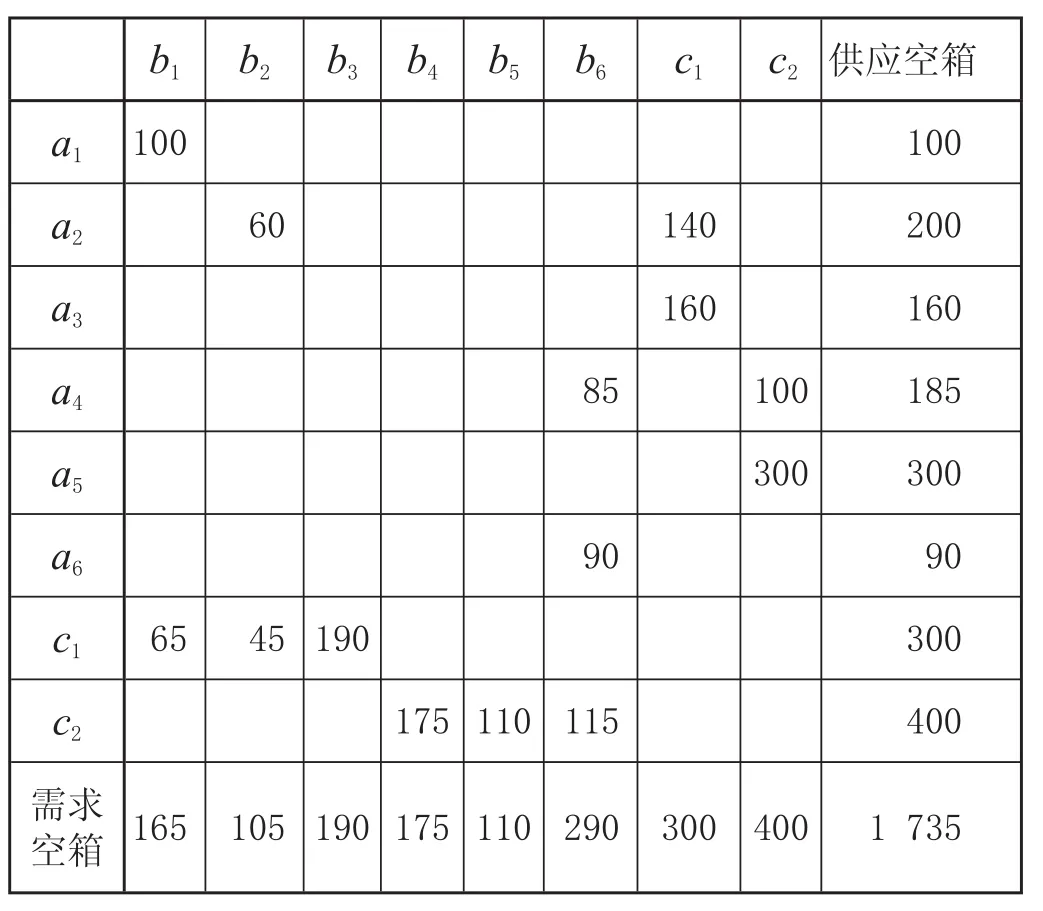
表2 最优配空方案 TEU

4 结束语

铁路集装箱运输中的空箱调整是一个复杂的、受多种不确定因素影响的多目标优问题，涉及车流组织和调度指挥等运输组织环节。在实际空箱调整中，最短路径不一定是最经济合理的，应从空箱调整中产生的运输费用，以及各种因素对配空调整的影响波动和随机性进行深入研究。

[1]刘洪涛. 技术计划空箱调整的数学模型[J]. 铁路计算机应用，2005(7)：21-23.

[2]杜艳平，尹晓峰，刘春煌. 采用蚁群算法求解铁路空箱调整问题[J]. 中国铁道科学，2006 (4)：119-122.

[3]林柏梁，乔国会. 基于线路能力约束下的铁路空箱调配迭代算法[J]. 中国铁道科学，2008(1)：93-96.

[4]闫海峰，谭云江，朱健梅. 铁路空箱调整蚁群算法的研究[J]. 铁道运输与经济，2006，28(8)：31-34.

[5]张金阁，程学庆. 带有技术站改编的空箱调整研究[J]. 铁道运营技术，2007(4)：12-14.

[6]谢金星，薛 毅. 优化建模与LINDO/LINGO软件[M]. 北京：清华大学出版社，2005.