基于滑移线场理论的边坡稳定性有限元分析

李 凯,陈国荣

(1.安徽省交通规划设计研究院,安徽合肥 230088;2.河海大学土木与交通学院,江苏南京 210098)

运用有限元法进行边坡稳定性分析时,稳定分析研究集中在2个问题上,一是安全系数,二是确定临界滑动面.有些方法从安全系数入手,如建立在极限分析理论上的强度折减法[1-3],就是通过对材料强度参数的折减,直接计算安全系数.同样,如果能求得滑动面,也可以容易地计算出安全系数.目前搜索滑动面的方法主要分为模式搜索法和数值规划法.数值规划法在我国应用较早.该方法把滑动面的函数看成变量,把安全系数看成这些变量的泛函,通过变分法寻找安全系数最小时对应的滑动面.

试验证明,岩土中有一点遭到破坏的时候,该点必然存在2个破裂面.在二维空间里,可以用2条相交的直线表示这个点的破坏方向,经典塑性理论抽象地称之为滑移线.假如把整个区域离散成很多点,所有的点都发生破坏,就能得到这些破坏点的滑移线场.根据该滑移线场的走势,可以从宏观上分析整个区域破坏的轨迹.但是这个方法存在2个问题:(a)经典滑移线理论是建立在Mohr-Coulomb准则上的,由于Mohr-Coulomb准则在 π面上是不规则图形,不适合数值计算,为了和有限元结果耦合,需要建立理论上更完善的滑移线场方程.(b)边坡很多部分仍然在弹性状态下,这时传统的滑移线理论和现实存在较大的差异,要求对滑移线理论进行合理的拓展.

文献[4]将经典滑移线理论加以推广,提出了潜在滑移线理论;文献[5]发展了一套基于滑移线场理论的搜索临界滑动面的数值方法.本文在文献[4-5]的基础上,引入统一材料参数定义,依据统一屈服准则建立适合数值计算的全区域滑移线场方程.再根据有限元计算结果数值模拟滑移线场,由滑移线场追踪出临界滑动面,求得安全系数,并在此基础上讨论屈服准则的影响.

1 统一平面滑移线场理论

1.1 塑性区的滑移线场

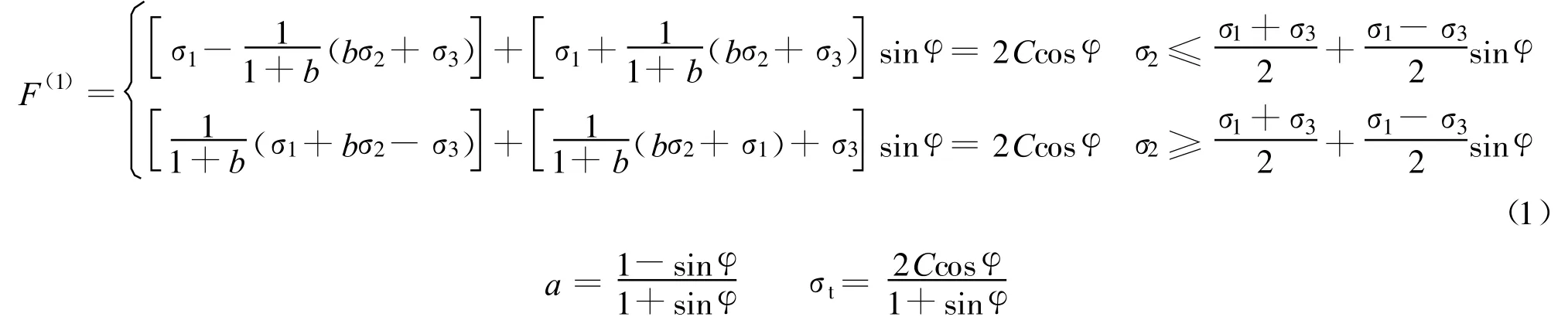
材料的屈服准则是材料破坏的判定标准,为了方便全面分析,采用双剪统一强度理论[6]:式中b(0≤b≤1)是一个加权参数,反映了中间剪应力及相应作用面上的正应力对材料屈服或破坏的影响.随着加权参数b值的不同,双剪统一强度理论可以分别蜕化成Tresca准则(当a=1,b=0时)、Mises准则(当a=1,b=1/2或b=1/(1+3)时,为线性逼近)、Mohr-Coulomb理论(当a≠1,b=0时).当b取其他不同值时,可以得到一系列新的强度准则.

根据Prandtl-Reuss假设[7]

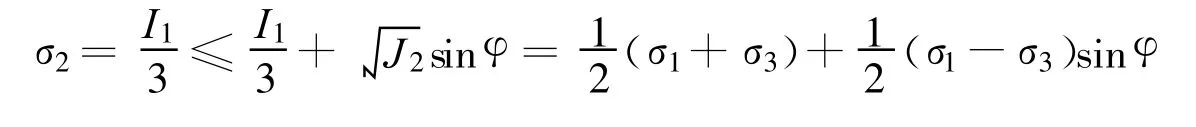
式(1)可以写成

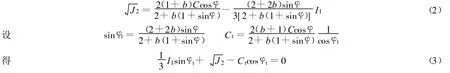
式中:φ,C——初始材料参数;φt,Ct——统一材料参数;J2——应力偏量的第2不变量,以逆时针方向为正.式(3)和岩土有限元分析中常用的DP准则形式相近,可以方便地引入数值计算中.将式(3)代入平衡方程:

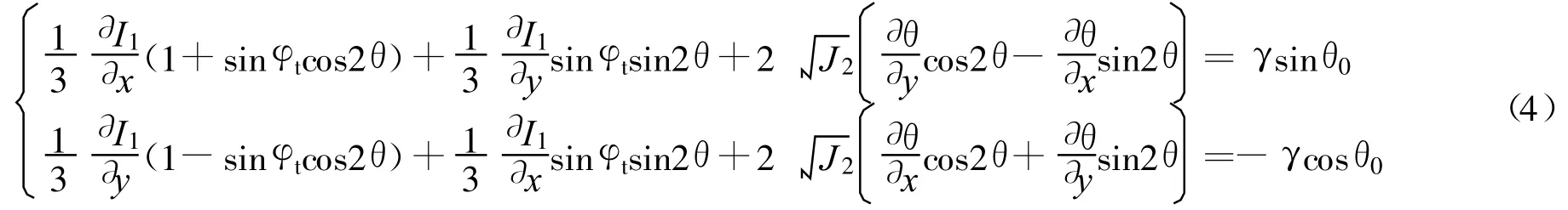
式中:θ——x轴和σ1之间的夹角;θ0——重力的反方向和y轴之间的夹角.式(4)通过特征线的方法求解[8-9]

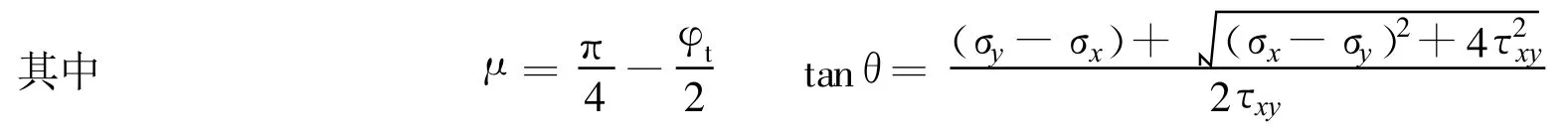
式(5)是控制方程(4)的2个不同的实数根,依据经典塑性理论定义,式(5)也称为滑移线方程[9],即塑性区域内的滑移线方程.滑移线见图1.

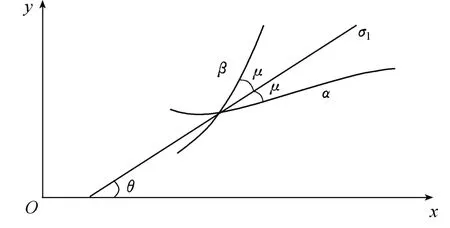
图1 滑移线和主应力迹线Fig.1 Slip lines and traces of principal stresses

1.2 弹性区的滑移线场

当材料处在弹性区间内,虽然没有发生破坏,但材料内过每一个点的无数个面上肯定有个面最容易发生破坏,称之为潜在滑动面[10].由于边坡破坏一般是剪切破坏,定义安全系数F为最大剪应力和实际剪应力的比,那么安全系数最小的面最容易发生破坏.定义α为这个面的方向角,得到

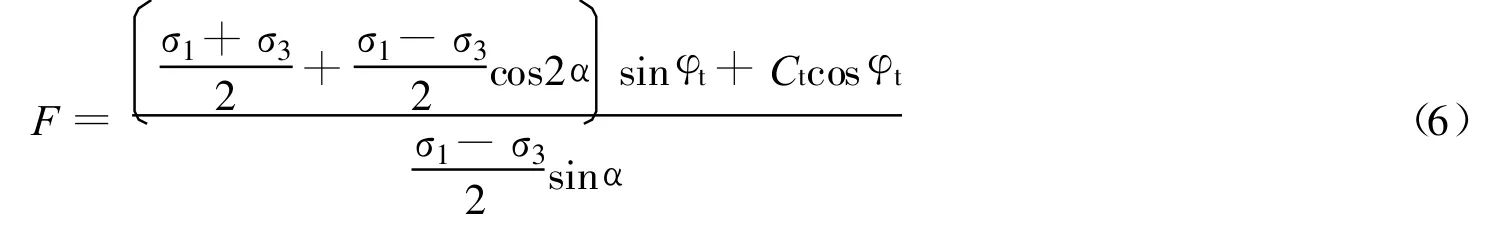
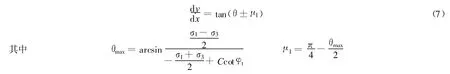
这样式(5)和式(7)即为全区域的滑移线方程(下文将滑移线、潜在滑移线统一称为滑移线).

2 数值模拟滑移线场和搜索临界滑动面

2.1 模拟滑移线场

本文是从宏观上分析全区域破坏的迹线,所以首先需要模拟出全区域的滑移线场.将模型离散,利用有限元计算软件ANSYS分析出各个离散点的应力和坐标值.为了便于编程处理,节点要规则分布,如图2所示.

塑性区间由式(5)、弹性区间由式(7)就能得到每个离散点的dy,即dx每个离散点的滑移线方向 φ,过该点和该方向可画出该点的滑移线,控制线长可得到全区域滑移线场示意图(图3).

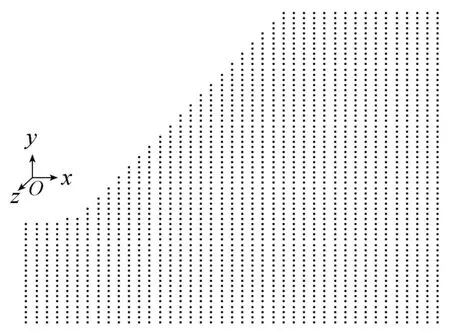
图2 离散点Fig.2 Discrete nodes

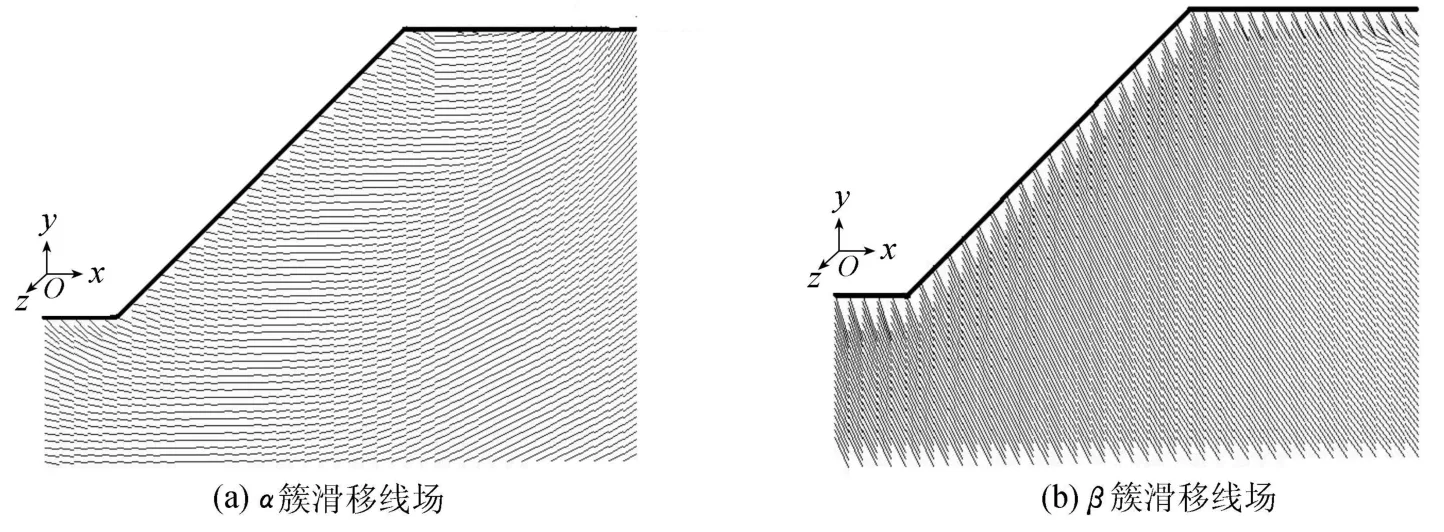
图3 滑移线场示意图Fig.3 Slip line fields

2.2 搜索临界滑动面

有2个滑动场,按工程经验选择1个进行分析,然后通过滑移线场追踪滑动面.如图4所示,离散点规则排列,从出口的一点A出发,点A坐标为(x,y),方向为φ,以此作一条直线.这条直线和经过邻近一竖列离散点的直线交于B(x1,y1).B点不一定是给定的离散点,但它必定在2个离散点之间.设这2个离散点为C(x2,y2),D(x3,y3),方向为 φ2,φ3,通过插值法就可以求出点B的滑移线方向φ1:

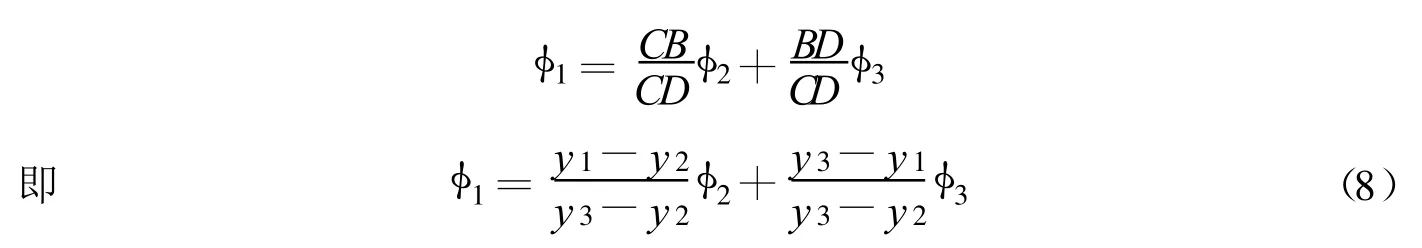
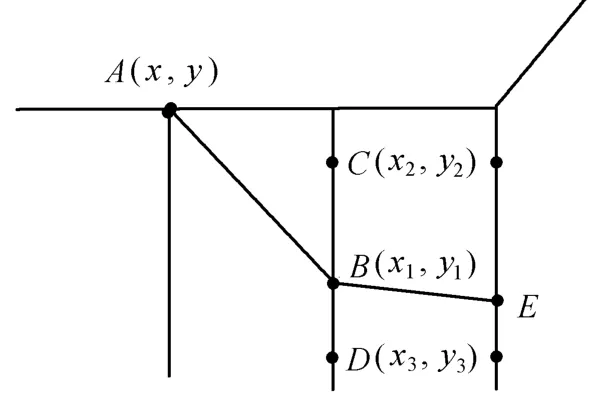
图4 追踪示意图Fig.4 Pursuing of slip surface

依次类推,得到E点,一直追踪下去,就可以得到1条连续的曲线.设定不同的起点,可得到一系列曲线,称之为潜在滑动面.在这些滑动面上,每个点的正应力 σ和剪应力τ也可以按相同的插值法求出.由抗剪安全系数F可得到这些潜在滑动面的安全系数:

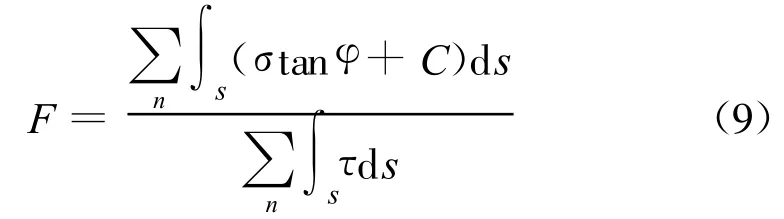
其中安全系数最小的就是临界滑动面,如图5所示.

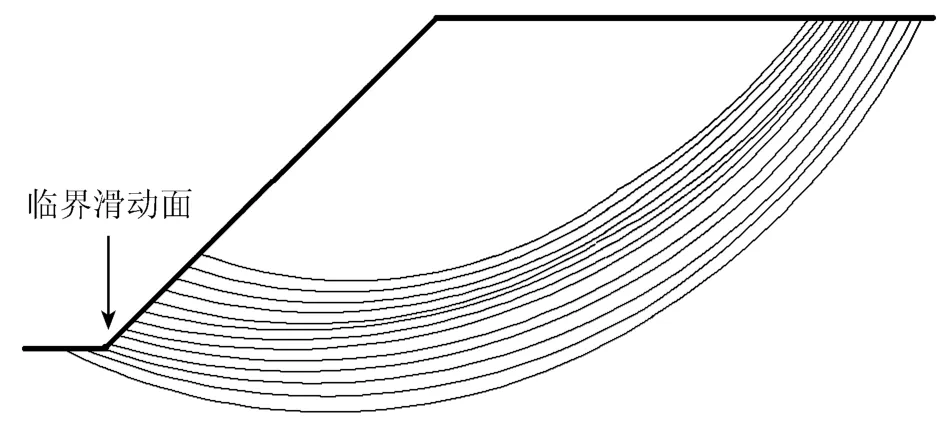
图5 滑动面示意图Fig.5 Slip surface

3 算 例

某一均质土坡,坡高H=20m,黏聚力c=42kPa,土的密度 ρ=2000t/m3,内摩擦角 φ=17°,泊松比 ν=0.3,弹性模量E=100MPa,求坡角 β=45°时边坡的稳定安全系数以及对应的滑动面.取b=0,0.2,0.4,0.6计算,得到统一材料参数φt和材料参数b的关系,见图6.

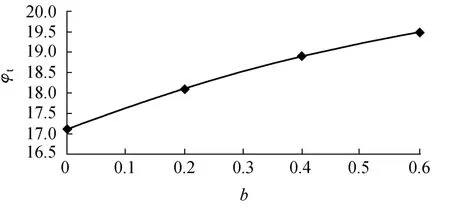
图6 φt和 b的关系Fig.6 Relationship between φtand b

运用ANSYS软件计算出离散点的应力值和弹塑性区间,按上文讨论的方法编程计算出最小安全系数,并和Spencer法[11]计算的结果比较.当b=0,0.2,0.4,0.6时,最小安全系数分别为1.182,1.210,1.232,1.246,而用Spencer法的计算结果为1.206.

图7(a)为b=0.2时的临界滑动面计算结果,图7(b)为该条件极限状态下的塑性区间分布,图7(c)为b不同取值时的临界滑动面.

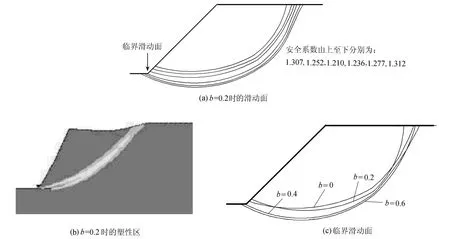
图7 计算结果示意图Fig.7 Calculated results

从图7可看出,临界滑动面贯穿于塑性带内,说明求得的临界滑动面位置是合理的.另外,临界滑动面和它上下2条潜在滑动面的安全系数相差不大,而且都处在塑性区内,表示它们都有可能发生滑移,滑移不一定是在一个面上,而是有一定厚度的,这比较符合实际情况.通过和Spencer法的比较,证明了本文方法计算结果的有效性,统一材料参数 φt和 φ差别不大,不同屈服准则下安全系数和临界滑动面的位置发生了改变.

4 结 语

本文建立了统一屈服准则下、适合数值计算的全区域滑移线场方程,根据有限元计算的结果数值模拟全区域的滑移线场,由滑移线场搜索出临界滑动面并计算安全系数.该方法无需假设滑动面和考虑弹塑性区域的差别,使用方便.算例证明了该方法的有效性,拓宽了经典的滑移线场理论.通过改变b值引入不同的屈服准则,研究屈服准则对边坡稳定性分析的影响,发现在不同的屈服准则下,安全系数和临界滑动面发生了改变.

[1]GIFFITHS D V,LANE P A.Slope stability analysis by finite elements[J].Geotechnique,1999,49(3):387-403.

[2]DAWSON E M,ROTH W H.Drescher slope stability analysis by strengthreduction[J].Geotechnipue,1999,49(6):835-840.

[3]郑颖人,赵尚毅.有限元强度折减法在土坡与岩坡中的应用[J].岩石力学与工程学报,2004,23(19):3381-3388.(ZHENGYing-ren,ZHAO Shang-yi.Application of strength reduction FEM in soil and rock slope[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(19):3381-3388.(in Chinese))

[4]张国祥,刘宝琛.潜在滑移线法分析边坡滑动面及稳定性[J].土木工程学报,2002,35(6):82-85.(ZHANG Guo-xiang,LIU Bao-chen.Analysis of slope slip surface and stability by the potential slip surface theory[J].China Civil Engineering,2002,35(6):82-85.(in Chinese))

[5]朱以文,吴春秋,蔡元奇.基于滑移线场理论的边坡滑裂面确定方法[J].岩石力学与工程学报,2005,24(15):2609-2615.(ZHU Yi-wen,WU Chun-qiu,CAI Yuan-qi.Determination of slip surface in slope based on theory of slip line field[J].Chinese Journal of RockMechanics and Engineering,2005,24(15):2609-2615.(in Chinese))

[6]俞茂宏,杨松岩,刘春阳,等.统一平面应变滑移线场理论[J].土木工程学报,1997,30(2):14-26.(YU Mao-hong,YANG Songyan,LIU Chun-yang,et al.Unified plane-strain slip line field theory system[J].China Civil Engineering,1997,30(2):14-26.(in Chinese))

[7]JOHNSON W,MELLOR P B.Engineering plasticity[M].New York:Van Nostrand Peinhold Company,1973.

[8]郑颖人,龚晓南.岩石塑性力学基础[M].北京:中国建筑工业出版社,1989.

[9]龚晓南.土塑性力学[M].杭州:浙江大学出版社,1990.

[10]张国祥,刘新华,魏伟.二维边坡滑动面及稳定性弹塑性有限元分析[J].铁道学报,2003,25(2):79-83.(ZHANG Guo-xiang,LIU Xin-hua,WEI Wei.Analysis of elastic-plastic finite element for two dimension slope slip surface and stability[J].Journal of the China Railway Society,2003,25(2):79-83.(in Chinese))

[11]SPENCER E.A method of analysis of the stability of embankments assuming parallel interslice forces[J].Géotechnique,1967,17(1):11-26.