一种交互式呈现渐进网格算法
求 伟, 张 帆
(武警杭州指挥学院,杭州 310023)
0 引言
计算机图形学中,常用Hoppe提出的渐进网格数据结构实现对复杂模型的细节分层。渐进网格由一个粗略的基网格和逐渐增加细节内容到网格中去的顶点分裂信息两部分组成。渐进网格可以基于观测标准,根据需要把细节加入到网格中,减少呈现时间;能在不同细节层次间实现光滑变化等等。然而,渐进网格数据必须同时全部装入内存,在呈现包含上百万个三角网格模型时,可能需要几个G内存空间,超出了当前许多机器主内存;另外大模型产生渐进网格耗时长。网格适应内存需求,不仅是简单的理论问题。本文从不把整个模型装入内存出发,在呈现方面进行了改进:通过系统平台装载当前需要的细节数据,减少内存需求,加快呈现速度,同时又不以输出品质为代价,实现渐进网格交互式呈现模型快速算法。
1 有关研究
交互式呈现呈现大模型方面技术有很多,如结构预排和点呈现。许多结构预排算法,不必把整个模型数据装载入内存,允许对模型进行交互;把数据放入分级结构中,执行内存管理,在适当的时间预取数据。重点在对内部重建上,模型通常由离散小片组成。因为典型地使用静态标准表示细节,有很多的解决方法,内存管理较容易。最后,依靠厚度可见选择,使用方法对内部进行处理。本算法在许多方面不同于结构预排,如模型由大块组成,采用连续变化的细节分层,而在厚度方面没有设计要求。点呈现技术使用点代替多边形呈现基本的原始的网格,是呈现大模型一个相当困难的技术。仅管已经有一些算法成功把这一技术应用于大模型,但得到的图象质量与采用多边形表示的还是有所不同,不一定能满足某些特殊要求。而且,现有的用于多边形呈现模型的加速器或设备驱动程序优化技术,不能优化点呈现。
2 交互式呈现设计
渐进网格可能包含了很多的细节,数量非常大,不能适应主存储器,其实用户需求可能没有那么多,并不需要把整个网格装载入内存。例如,观测者离网格很远,可以只用基网格表示模型;需要放大网格的某一部分,只要装载特定部分的细节等等。因此,考虑视点位置和屏幕空间误差,给定特定的位置和方向,在呈现时,只要装载渐进网格需要的部分,减少内存需求。接下来只要解决:怎样快速决定网格需要装载的部分;怎样装载和卸载网格,防止编码访问网格当前不用装载的部分。
2.1 模型前期处理
简单介绍模型前期处理,使用可以处理任意网格的Voronoi结构分割原始网格,输入时把模型分成相邻小块,同时对每一块进行简化;在分级时,把已简化的分块合并成原来大的块。算法如下:
1)给定一个需要缝合的分块列表。在同一时间处理这些输入块,每遇到一个顶点就基于它的位置把它加入表中。2)如果这个点已存在表中,那么这个点是双重点,如在同一块中被两个面使用,或在边界上被多个块用到的点,对双重点进行处理。3)如果一个顶点不是双重点,那么给它指派一个ID。如果是双重点,使用前面已指派过的ID。这样,合并后网格与原始网格具有相同顶点,可顺利地被调配,再次作为独立顶点处理。
要注意的是,不能简化块边界,如果允许简化边界,分块边拓扑会改变,而点和面相对线性无关,简化算法也会失败。合并处理无论在运行时间还是内存使用上都相当有效,采用表检测双重点只装载一次基网格,占用时间少,内存使用也小。通常在最后内存需求最大,因为顶点分裂作为合并后的结果已发生了改变,必须进行重新编号后,还有面ID值。当然,对于要求不高的情况下,这一步也可以省略,或是以后的一个改进方向。
2.2 确定装载对象
理想状态下,给定一个观测点,主存储器要包含需要精确呈现的面和点。通常需要对网格逐面进行判断确定装载和卸载的数据,效率非常低。决定装载哪些面需要很大开销,每次装载和卸载一个面设计不合理。另外,维持一致的数据结构会变得非常复杂。算法考虑不依靠面,在块呈现上对数据进行装载和卸载处理。在分块层级上精化块,简化单个分块时,输出一系列顶点分裂。渐进网格中面、顶点和顶点分裂关系如图1所示。
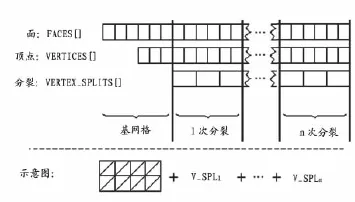
图1 面、顶点和顶点分裂数组及分层呈现关系
每一层细节呈现,只是作为渐进网格面、顶点和顶点分裂这些数组中的一组元素进行存储。明确观测者的位置和方向,进行可见性检查,确定网格中每一个分块是否需要装载。一个块仅在:分块位置可见或用户需要分块中的细节两种情况下装载。第二种情况与屏幕允许空间误差容忍量,块的最大残留,观测者和块间最小距离等因素有关。确定最大误差和最小距离的目的是防止装载过于详细的信息,而对观测者位置来说微不足道。
确定当前是否要装载一个分块细节以外,在一定范围内基于观测者位置和方向会发生变化,还要确定在可能变化范围内,下一步装载分块细节,在需要时装载预取的块细节。考虑观测位置和方向变化、确定可见性、最大误差和最小距离等因素,需要大量计算,影响预取数据速度,精确要求却不高。可以根据每个分块都是一个立方体,对分块细节设定一个近似空间范围,在最后进行少量相交测试简化计算。实验数据表明这样的处理是有效的,可以达到快速决定分块细节是否需要装载的目的。进行这个简单测试后,在每个画面呈现之前对所有的网格分块细节进行循环,决定哪一块装载和卸载,工作量的大小和块细节的数量有关。
2.3 装载和卸载数据
确定一个分块细节需要在内存处理后,执行装载和卸载,要保持数据结构的一致性,防止访问没有装载的部分。渐进网格的数据结构粗略地组织如图1所示,平行排列面,顶点和顶点分裂信息。每个顶点分裂有两个面索引和两个顶点索引与之相关联。分块细节按顺序存储,可以看作是行里的列元素,而装载和卸载分块细节可以看作是装载和卸载数组的某个部分。对局部数组装载,使用函数VirtualAlloc()和VirtualFree(),允许存储整个数组虚拟地址空间,然后指派和释放大量内存。单个块细节呈现则使用邻近区域的虚地址空间,因为要考虑减少内存冲突的可能性;以及不通过间接分层,访问数组里特定元素。
下面是装载一个分块细节的步骤:
1)使用VirtualAlloc()给数组中需要的行指派内存;
2)在数据文件中寻找分块细节的开始处,读取数据,写入数组,位置在网格文件第一次装载时已存储;
3)对每个装载的顶点,更新父顶点表示当前可以进行分裂。也就是它的子顶点都装载进内存了,而每个父顶点的ID是存贮在硬盘数据文件中的。
卸载一个分块细节类似,步骤如下:
1)对每一个要卸载的顶点,更新父顶点,表示它不能进行分裂,也就不必装载相关的子顶点和面。
2)使用VirtualFree()给数组中需要的行释放内存。
要注意的是,利用虚地址空间来存储数组,整个网格大小受到可用的地址空间数量的限制。在32位以下的操作系统,网格大小不能超过2GB,64位以上则不受这个限制,当前硬件技术的发展可以完全不受这一限制影响。
3 呈现结果
本算法呈现过程中,内存使用比其它装载整个网格的算法要低。呈现效果需要使用多种的数据检测,也会因很多因素而不同,如观测者的需要,创建网格时块尺寸的选择、简化参数的使用等。在一个特定观测场合试验,如图2,依次为观测者由远至近移动位置显示的图片效果,以及呈现的面和所需的内存,没有装载模型中不需要呈现的部分,减少了内存使用,结果表明使用部分数组装载得到了预期效果。
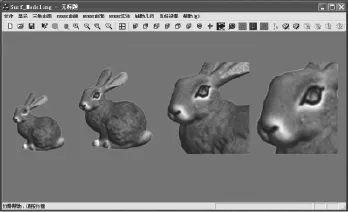
图2 观测者由远至近移动位置显示的图片效果
呈现速度方面,部分数组每一块需要被装载时,如果每块细节特别小会引起一个短暂停,可通过执行块异步块装载设计消除。简化预处理时,所做的一些选择,也会直接影响呈现结果。在分块大小以及一些参数等方面进行认真选择很有必要,否则,可能会出现一个非常大的基网格,或是在每一分块呈现太多太少的数据,反而可能降低呈现速度。
4 结束语
当前呈现时没有限定内存,如果在这方面进行一定研究,将会带来更多便利。考虑可以动态调整屏幕空间误差,当可用内存变低时就逐渐增加,减少装载块呈现。另外,考虑观测者的速度和加速度,改进块装载和卸载设计,呈现将可能只需要预取块,对合理使用系统内存更有效。
[1] Hoppe H,Progressive meshes,ACM SIGGRAPH 96 Conference Proceedings,ACM SIGGRAPH,1996,99–108,121–26.
[2] Stephan Bischoff, Leif Kobbelt, Teaching meshes,subdivision and multiresolution techniques,Computer-Aided Design 36 (2004)1483–1500.
[3] Josef Kohout, Selected Problems of Parallel Computer Graphics,Technical Report No.DCSE/TR-2004-02,March,2004.
[4] Hong Tzong Yau,Chuan Chu Kuo,Chin Hsiung Yeh,Extension of surface reconstruction algorithm to the global stitching and repairing of STL models,Computer Aided Design 35(2003)477-486.
[5] Peter Szinek,Optimized Subdivision Surface Displaying,Master Thesis of Comenius University Bratislava, Faculty of Mathematics,Physics and Informatics,Department of Geometry,Bratislava,April 2003.
[6] 郑君立,海量数据点三维重构关键技术研究与应用[D].东南大学,2003.
[7] 陈涛.逆向工程中数据分块和规则曲面拟合算法的研究[D].南京航空航天大学,2004.
[8] 王霄.逆向工程技术及其应用[M].化学工业出版社,2004.
[9] 戴静.逆向工程数据处理关键技术研究[D].南京理工大学,2003.
[10]张杰.由散乱点生成三角网格曲面的算法研究与实现[D].北京大学,2003.

