基于粒子群优化径向基神经网络在模拟电路故障诊断中的应用

操建华

（顺德职业技术学院 电子工程系，顺德 528300）

0 引言

在模拟电路的故障诊断中，传统的分类及诊断都需要大量的计算，特别是由于容差的影响，其计算相当复杂，实用性较差。神经网络具有对信息的高度并行处理能力、极强的自适应能力、非线性映射能力等，因此神经网络在故障诊断中得到了很好的应用并成为一种理想的故障诊断方法[1]。目前，在各种类型的神经网络中，BP网络因其有极强的非线性映射能力而最适合于解决分类问题，但是BP神经网络有输入数目多、结构难以确定训练时间过长等缺点，RBF不仅具有上述优点，同时在学习速度上具有优势。故其在故障诊断中被广泛采用。粒子群算法（PSO）采用速度—位移搜索模型，计算复杂度低，通过群体中粒子间的合作与竞争来搜寻全局最优解。用PSO算法来训练神经网络，可以充分发挥粒子群算法全局的寻优能力和局部的快速收敛优势，提高了神经网络的泛化能力和学习能力[2]。

1 RBF神经网络

如图1所示，RBF神经网络是一个三层前馈神经网络，它的基本思想是用径向基函数作为隐单元的“基”，构成隐含层空间，隐含层对输入矢量进行变换，将低维的模式输入数据变换到高维空间内，使得低维空间内的线性不可分问题在高维空间内可分。它包括输入层、隐含层和输出层，其中各层节点数分别为k、n、p。故障特征向量作为输入层节点，由X=[x1,x2,,…,xq…xk]T，故障类别作为输出层缺点，由Y=[y1,y2…yj…yp]T表示。网络的隐含层

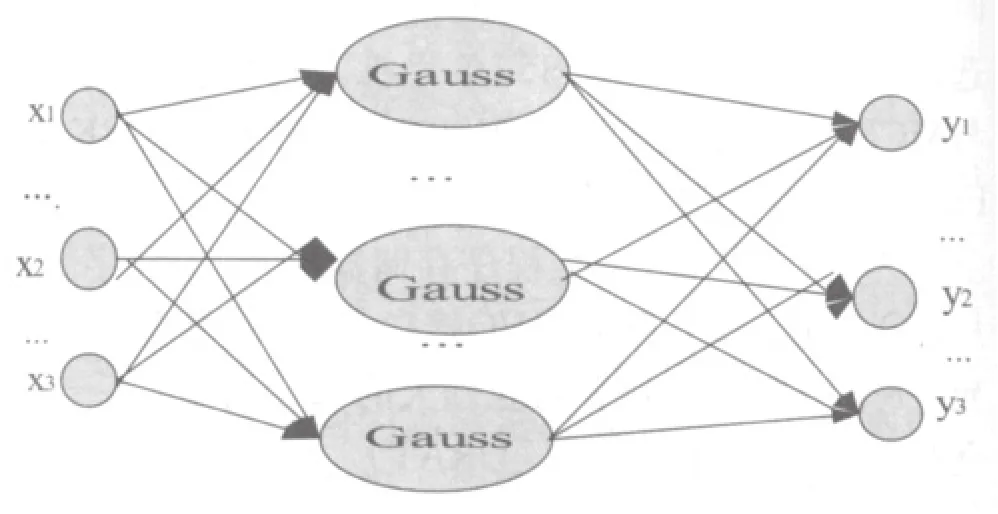
图1 RBF神经网络结构图

输出，即径向基函数的输出只依靠输入矢量与径基函数中心的距离，选用高斯（Gauss）函数作为径向基函数（如式1）

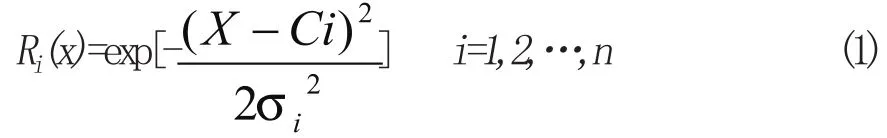
距离用欧氏范数表示，当网络输入为XK时，则隐含层的输出为

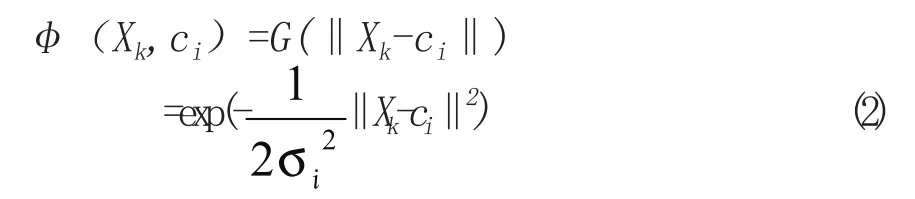
其中，ci=[ci1,ci2, … ,cIm]T为高斯基函数的中心；σi为高斯函数的方差。

输出层是对线性权值进行调整，采用的线性优化策略，因而学习速度较快。令输出为YJ(X),则：

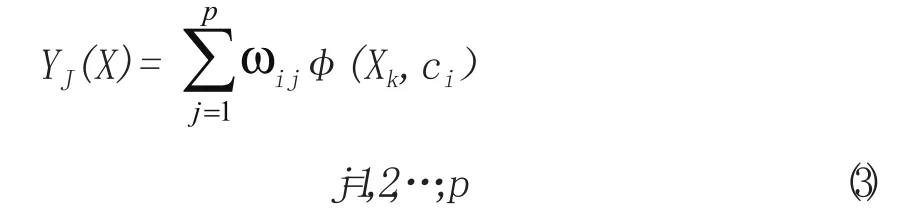
其中，ωij为连接隐含层和输出层的权值。

2 粒子群优化算法

粒子群优化（PSO）算法是Kennedy和 Eberhart于1995年提出来的，该算法是模拟鸟群寻找栖息地的行为，通过搜寻各个粒子的优解和利用这些优解使整个粒子群达到最优的过程。PSO是基于群体智能理论的优化算法。每个粒子代表解空间的一个候选解，解的优劣程度由适应函数决定。

在粒子群算法中，设搜索空间为D维，粒子数为N，第i个粒子经历过的最好位置记为Pi=(Pi1,Pi2,…,PId),即Pbest,可以看作是粒子自己的飞行经验；在群体所有粒子经历过的最好位置用g表示，即Pg,也就是全局极值gbest,可以看作是粒子同伴的经验[3]。

在找到两个极值后，粒子根据如下的两个公式式（4）和式（5）更新自己的速度和位置：

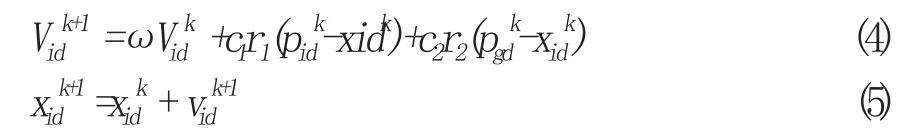
其中，v是粒子的速度；x是粒子的当前位置；Pbest和gbest如前面定义；r1和r2是介于（0，1）之间的随机数值；c1和c2是学习因子，通常一般等于并且在0和4之间；ω是惯性权重，它具有维护全局和局部搜索能力的平衡的作用。为了在前期有较高的探索能力以得到合适的粒子，在后期后较高的开发能力以加快收敛速度，可将ω设定为随着进化而线性减少。此外，粒子的速度被一个最大速度限制，如果粒子当前速度超过最大速度，则该粒子的速度被限制在最大速度。

3 PSO优化RBF神经网络

3.1 分组优化策略

RBF网络的性能决定于网络的参数：即基函数的中心和方差以及网络权值。当权值的中心是都需要调整的参数时，RBF就是一个无约束的非线性优化问题。分组优化策略基于如下定理：

定理1：分组优化可以在同一次对各分组参数矢量寻优的过程中对每一分组参数矢量取得优化解。

定理2：对无约束优化问题，分组优化取得的解是原问题优化解的充要条件，各分组参数矢量的解为该分组参数矢量对应的仅以该分组矢量为自变量的优化问题的优化解[4]。

3.2 PSO-RBF算法

PSO-RBF算法首先对初始权值进行优化，在解空间中定位出一个较好的搜索空间，然后用RBF算法在该小的解空间中搜索出最优解。步骤如下[5～8]：

1）将基函数的中心和方差以及网络权值作为参变量，进行实数编码。

2）在编码的解空间中，随机生成初始种群。

3）对群体中的每个个体进行适应度评价，如果好于该粒子当前的最好位置的适应度，则更新该个体的最好位置。如果所有的粒子的最好位置的适应度好于当前全局最好位置的适应度，则更新全局的最好位置。

4）用公式（4）和（5）对每个粒子的速度和位置进行更新，产生下一代的粒子群。

5）如果当前的迭代次数达到预先设定的最大次数，则停止迭代，在最后一代找到全局最优解的近似值，否则，跳转到步骤（3）和（4），重复进行。

6）将PSO优化后的将基函数的中心和方差以及网络权值作为RBF网络的初始值，对神经网络进行初始化。

7）利用RBF算法进行训练，直到误差收敛到设定的精度，训练结束。

4 实例分析

以中心频率25KHZ、带宽50KHZ的带通滤波器作为诊断实例，如图2所示。使用PSpice软件对电路进行仿真，求出正常状态和各种故障状态的理论值。在上述电路图中，电阻和电容的容差分别为±5%和±10%，在此范围内变化，滤波器的输出认为是正常的。在这里，我们仅仅考虑R3、R4、R5和C1超出容差范围的单故障。同时，可以将故障分为8个故障模式：↓R3、↑R3、↓R4、↑R4、↓R5、↑R5、↓C1、↑C1。其中，↓表示容差低于允许容差的低值，↑表示容差高于允许误差的高值。8中故障模式在加上正常状态，共9种模式。因此，我们可以用4位2进制数来表示9种模式，如表1所示，所以该神经网络的输出层为4个，在待测电路的输出响应中选取5个点来描述输出响应的波形曲线，所以选取网络的输入个数为5，经过试验，网络的隐含层神经元的个数为18个。

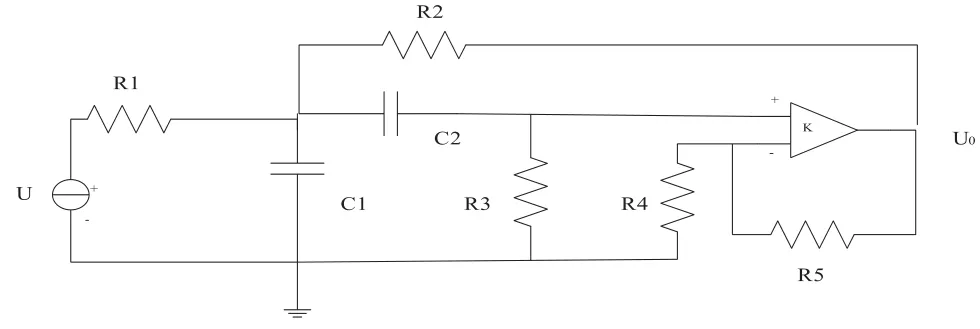
图2 带通滤波器

表1 故障状态的二进制表示

为检验基于PSO优化的RBF神经网络的快速学习能力与故障诊断效果，在误差为0.02时，分别使用训练模式和测试模式对网络进行测试[9～10]，结果见表2。图3示了误差指标设定为0.02时的误差变化曲线图，表3显示了在误差指标为0.02时，神经网络的用于模拟电路故障诊断的学习速度和诊断正确率。

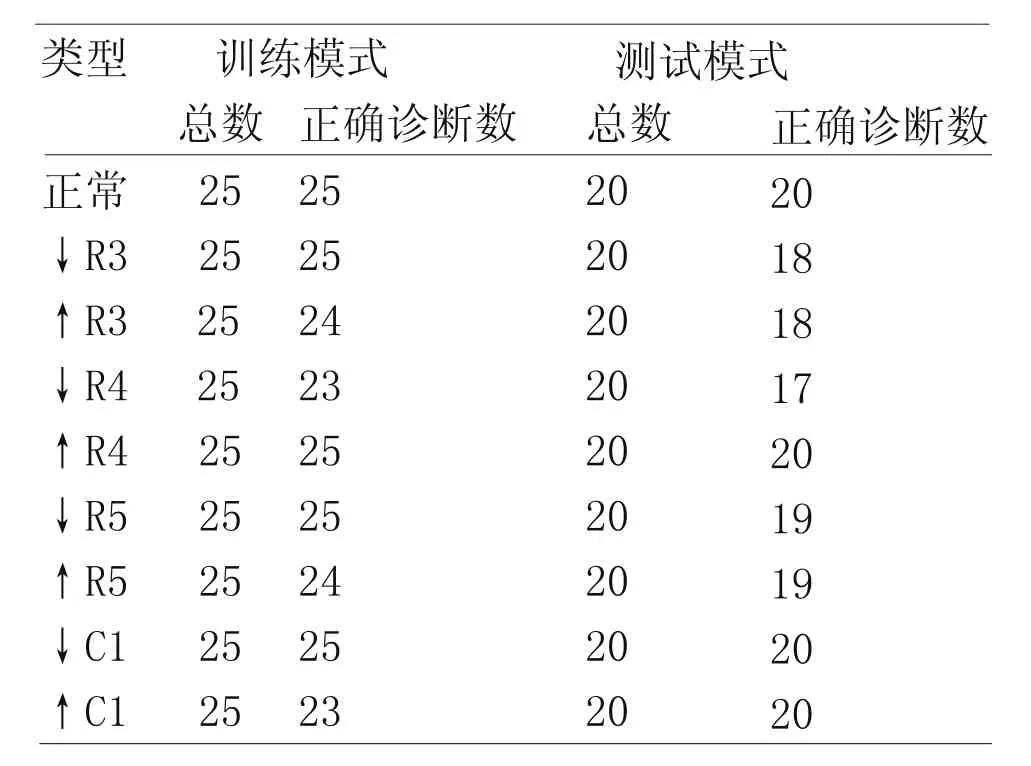
表2 期望误差为0.02时神经网络的诊断结果

表3 神经网络的训练次数与诊断正确率

5 结束语

文章介绍了一种基于粒子群优化的径向基神经网络的模拟电路故障诊断方法，利用了PSO操作简单，容易实现、收敛速度快的特点，成功地将此方法应用于实际的模拟电路中，实验结果表明，用PSO算法对神经网络进行优化，能使网络具有较高的精度，较快的收敛到最优解。该方法是可行的有效的。但该方法也存在不足，网络结构的选择对诊断率有较大影响，而且网络结构隐层单元的选择没有统一的标准。此外，故障设置仅仅选择了单故障模式，多故障模式没有进行讨论。

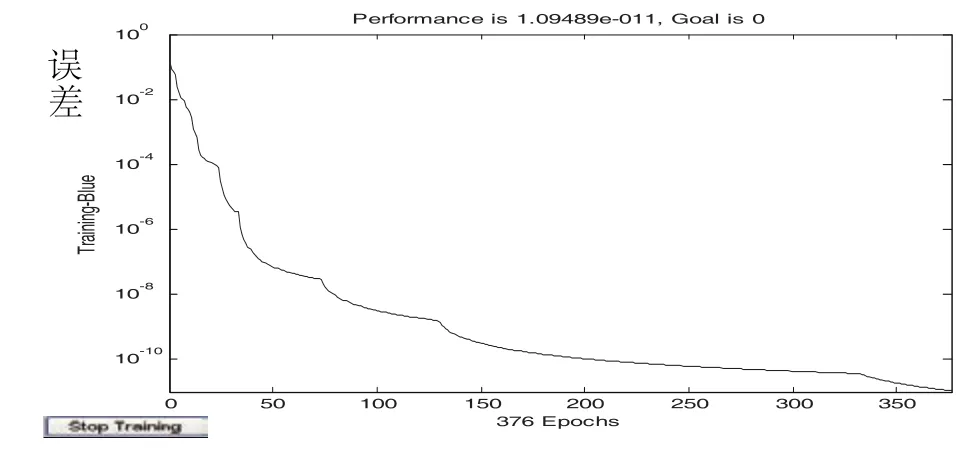
图3 误差变化曲线

[1] 杨士元,等.模拟电路软故障的研究[J].微电子学与计算机,2008,25(1):1-3.

[2] 刘洪波,王秀坤,孟军.神经网络基于粒子群优化的学习算法研究[J].小型微型计算机系统,2005,26(4):638-640.

[3] 曾万里,危韧勇.基于改进PSO算法的BP神经网络的应用研究[J].计算机技术与发展,2008,18(4):49-51.

[4] 李春明.模拟电路故障诊断的神经网络方法[J].内蒙古工业大学学报,2000,19(2):55-60.

[5] 王承,谢永乐.基于径向基函数神经网络的模拟/混合电路故障诊断[J].电路与系统学报,2007,12(2):66-68.

[6] 黄戈,崔建武等.基于粒子群优化神经网络的水轮机故障诊断[J].电网与清洁能源,2009,25(4):33-36.

[7] 杨士元,模拟电路的故障诊断与可靠性设计[M].北京:清华大学出版社,1993.

[8] 姚文俊,游正红.基于神经网络的模拟电路的故障诊断[J].中南民族大学学报,2004,23(3):23-28.

[9] 葛哲学,孙志强,神经网络理论与MATLAB实现[M].北京:电子工业出版社,2007.

[10] 飞思科技产品研发中心.神经网络理论与MATLAB7实现[M].北京:电子工业出版社,2005.