基于径向基函数神经网络的电机轴承智能故障诊断

孙 伟，柴世文，杨河峙

（1. 兰州工业高等专科学校 机械工程系，兰州 730050； 2. 甘肃省机械科学研究院，兰州 730030；3. 兰州好华齿轮有限责任公司，兰州 730050）

0 引言

轴承是电机主轴的支撑，是电机的重要部件之一。异步电动机的轴承故障发生概率约为40%，由于工作面接触应力的长期反复作用，极易引起轴承疲劳、裂纹、压痕等故障，将引起电机异常振动，电机将无法正常运行。这种异常振动超过常规振动所规定的允许值时，也会对电力生产及人身安全带来极大的危害甚至整机报废，造成重大事故。可见轴承工作状态是否正常，对于电机有着重大的影响。

目前，轴承故障可通过目测、测量和无损探伤等方法进行检测，但这些方法易受噪声干扰而产生误判。而神经网络的自学习能力、非线性映射能力、对任意函数的逼近能力、并行计算能力和容错能力等为构造新型故障诊断系统提供了有力手段[1]。本文采用基于径向基函数神经网络技术对作为电机主要支承型式的滚动轴承进行智能故障诊断。

1 径向基函数神经网络

径向基函数神经网络用径向基函数作为隐层单元的“基”，构成含层空间，隐含层对输入矢量进行变换，将低维的模式输入数据变换到高维空间内，使得在低维空间内的线性不可分问题在高维空间内线性可分。

1.1 径向基函数神经网络建模原理

径向基函数神经网络是单隐层的前向网络，它有三层构成:第一层是输入层，由信号源节点组成；第二层是隐含层，隐单元的个数由所描述的问题而定，隐单元的变换函数是对中心点径向对称且衰减的非负非线性函数；第三层是输出层，它对输入模式做出响应。径向基函数网络模型如图1所示。

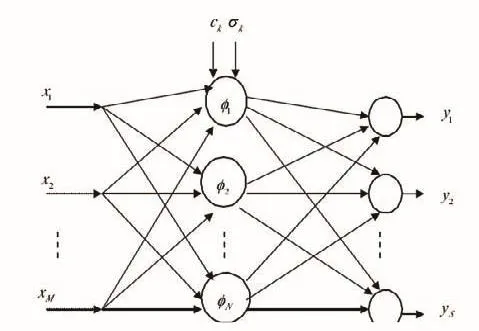
图1 径向基函数网络模型

1.2 径向基函数神经网络训练算法

径向基函数的Gaussian函数网络的学习参数有3个，即各径向基函数的中心Ck、方差σk和输出单元的权值Wk。径向基函数网络算法步骤如下[2-3]：

1）从输入向量中选一组初始中心值Ck；

2）计算方差值

式中dmax为最大的距离，K为Ck的数量；

3）由输入x(n)计算

4）更新网络参数

式中

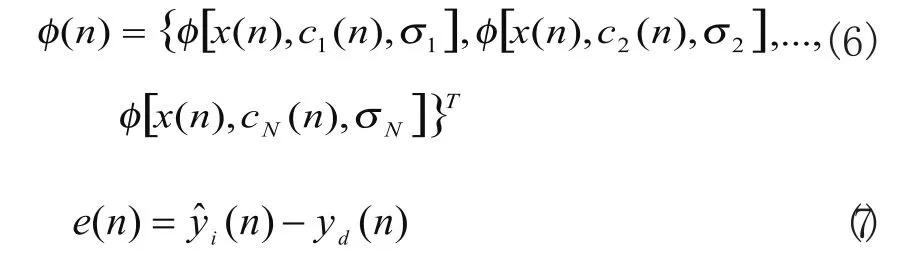
为网络期望输出； 为3个参数的学习步长。

5）如网络收敛，则计算停止，否则转到步骤（4）。

2 电机轴承的故障特征提取

本实验采用型号为6204的深沟球轴承，在电机驱动端轴承座上使用带磁座的电荷加速度传感器采集振动信号。考虑到生产现场很难搜集全各种故障数据，采用电火花加工技术在正常轴承各表面加工出细微的点蚀。轴承故障分为内圈故障、外圈故障、滚子故障、正常轴承4种状态。故障直径分别分为0.007inchs，0.014inchs，0.021inchs三个等级，深度都为0.011 inchs。马达电机负载分别在0，1，2，3HP下测得的，电机转速为1430rpm，其每一个状态如表1所示组合进行测试。然后采用小波包频带能量分析技术提取滚动轴承的故障特征[4]。

表1 试验安排状态表

3 电机轴承故障诊断仿真结果

通过调用MATLAB神经网络工具箱的newrb函数创建一个径向基函数神经网络，输入层神经元16个，输出层神经元16个，径向基函数的分布密度SPREAD=3，训练目标误差值取为0.0001。网络的输出模式，采用以下的输出模式：

滚动体故障：（1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0）；

内圈故障： （0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0）；

外圈故障： （0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0）；

无故障： （0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0）；

在训练的过程中，隐含层的神经元数量的确定是一个关键，传统的做法是使其与输入向量的元素相等，显然此方法在输入矢量过多时，过多的隐含层神经元让人难以接受。此处，隐含层的神经元从0个神经元开始训练，通过检查输出误差使网络自动增加神经元，每次循环使用，使网络产生的最大误差所对应的输入向量作为权值向量，产生一个新的隐含层神经元，然后检查新网络的误差，重复此过程直到达到误差要求或最大隐含层神经元数为止。

我们选择了80组训练样本时，73步达到训练目标，如图2所示。选用滚动轴承的48组测试样本送入训练好的径向基函数神经网络进行模式识别，诊断结果如表2所示。由表2可以得到径向基函数神经网络诊断准确率为97.91%。

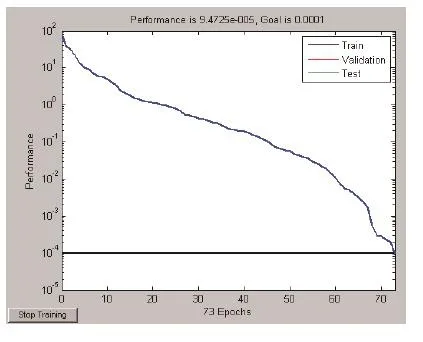
图2 径向基函数神经网络训练过程（SPREAD=3）

在径向基函数神经网络的设计中，最重要的参数是径向基函数的分布密度。为了验证径向基函数的分布密度的取值对故障诊断准确率的影响，分别取SPREAD=1，SPREAD=2，

表2 径向基函数神经网络诊断结果

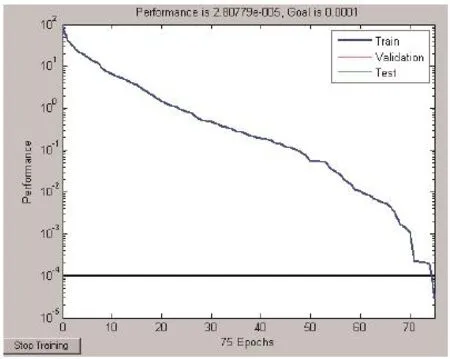
图3 径向基函数神经网络训练过程（SPREAD=1）

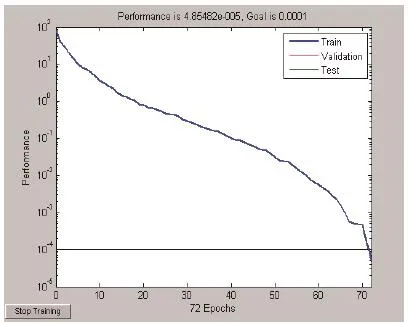
图4 径向基函数神经网络训练过程（SPREAD=2）

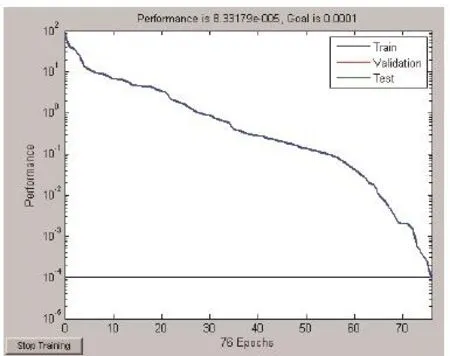
图5 径向基函数神经网络训练过程（SPREAD=8）

SPREAD=8，仍采用原训练样本和测试样本进行试验。图3、4、5分别为取SPREAD=1，SPREAD=2，SPREAD=8时径向基函数神经网络训练过程，当SPREAD=1时，径向基函数神经网络诊断准确率为93.75%；当SPREAD=2时，径向基函数神经网络诊断准确率为95.83%；当SPREAD=8时，径向基函数神经网络诊断准确率为97.91%。

4 结论

本文将径向基函数神经网络用于电机轴承的故障诊断，采用径向基函数神经网络对电机轴承在滚动体故障、内圈故障、外圈故障以及无故障状态给予识别。试验结果表明，系统不仅能够检测到轴承故障的存在，而且能够更高效、准确地进行电机轴承的故障模式识别，能够更好的应用于电机轴承的故障诊断中。

[1] 梅宏斌.滚动轴承振动监测与诊断——理论•方法•系统[M].北京:机械工业出版社,1996.

[2] Simon Haykin.Neural Networks:A Comprehensive Foundation (Second Edition) [M].Prentice Hall, 1999.

[3] Ham F M,Kostanie I,Priciples of Neuro Computing for Science& Engineering [M].McGraw Hill,2001.

[4] 温熙森,陈循.机械系统动态分析理论与应用[M].北京:国防工业出版社,1991.