两船在静水中的兴波干扰数值计算

王小龙 毕 毅

海军工程大学船舶与动力学院,湖北武汉430033

两船在静水中的兴波干扰数值计算

王小龙 毕 毅

海军工程大学船舶与动力学院,湖北武汉430033

使用VOF方法计算两排水量相当的船型在静水中兴波的水动力干扰,计算时采用两型值一样的Wigley船作为对象,湍流模式选择了RNG k-ε模型。在模拟计算时,变化两船的航速以及两船的间距,得到不同状态下的兴波波形。将得到的波形加以比较分析,进而得出兴波值最大的位置。低速时兴波最大值出现在距船首1/3船长左右的位置,高速时兴波最大值出现在距船首2/3船长左右的位置。将计算结果与实验结果相比较,令人比较满意,证明这种算法是很有效的,为以后的较为复杂的船型两船干扰模拟计算提供了一些参考。

VOF方法；Wigley船型；自由面；兴波干扰

1 引言

两体的水动力干扰研究早在上世纪60年代就已经发起了。Ohkusu［1］采用系列展开法计算作用在相互连接的两个圆柱体上的水动力。Van Oorhnerssen［2］采用三维源汇分布法计算了圆柱与方盒的相互干扰水动力系数并与模型试验结果进行比较。Kodan［3］采用切片法预报两体干扰问题,并且给出了两个结构体在不规则波中的响应结果。Loken［4］则采用三维源汇分布法分析了波浪中运动的多体之间的干扰。Duncan等［5］应用Van Oorlmerssen提出的方法计算了两舰之间的耦合运动响应。Korsmeyer［6］则采用试验的方法研究了两舰的垂向运动,并采用三维面元方法计算了两舰在有限水域的干扰问题。Williams与Rangapp［7］采用修正平面波方法计算了由多列半浸圆柱结构组成的多层柱海洋平台的水动力载荷与附加质量阻尼系数。Zhang等［8］采用基于B样条的一种新的数值方法计算三维船体水动力,用B样条函数表达三维船体表面的几何形状以及流场中未知物理量的分布,在一些假设下对两船作平行航行时的干扰水动力做了相应的计算工作。王建方等［9］基于线性势流理论,采用二维切片法(STF)研究波浪中两个浮体以相同航速航行时所产生的水动力干扰效应,通过数值计算预报两浮体的五自由度混合运动响应；提出了一种预报两舰在波浪中做耦合运动的三维频域方法。

以上的作者采取不同的研究方法,研究目的也不尽相同。随着大型船舶的发展,为了满足大型船舶海上补给的需要,其排水量与补给船处在同一数量级,因此,对于排水量相当的舰艇进行补给时的干扰问题的研究显得更加迫切。本文选择两个型值一样的Wigely船为研究对象,目的是为了研究排水量相当的船型在补给时的影响,何处出现比较大的波峰波谷,为两船补给时提供一个比较好的补给点,为后面的复杂船型的数值计算和模型实验提供参考。本文从静水兴波出发,研究探讨两船的干扰问题。数值模拟计算与双体船有相似之处,但是研究的方向是不同的,重点是研究两船兴波干扰时中间对称面的波形,而双体船主要是站在阻力的角度去研究。

2 数学模型和控制方程

绕船体的自由表面流动实际上是两相 (水和空气)流动,自由表面也就是水和空气的交接面。水是不可压缩流体；又因为给定的船速比较低,所以空气也可以作为不可压缩流体处理。

水和空气的连续方程分别可以用体积分数写为：其中,V→为速度矢量；α表示体积分数,下标a和w分别代表空气和水。

计算区域内的每个控制体积都由水和(或)空气充满,它们的体积分数之和应为1,即

两相流同样要满足动量守恒方程：

其中,流体密度ρ=αwρw+αaρa；p为压力；μ是粘性系数为重力加速度是体积力。

计算时的雷诺数分别为：3.0×106和4.28× 106。对于湍流模式,本文所应用的是k-ε方程模型的一种改进模式RNG k-ε模型,这种模型是一种适合复杂粘性流场计算的湍流模型［10］。其方程形式如下：

模型的边界条件的具体设置如下：

1)入口边界位于距船首一倍船长的地方,在入口边界,根据船体的运动速度,给定入口流体的流动速度,根据自由面的具体位置设置水和空气的体积分数。单船时,入口边界宽度为一倍船长(图1),两船时,入口边界宽度为一倍船长再加上两船间距的一半(图2)。

2)出口边界距船尾两倍船长,其流动不受船体的影响,流动是均匀的,并设置压力出边界条件,单船时,出口边界宽度为一倍船长(图1),两船时出口边界宽度为一倍船长再加上两船间距的一半(图2)。

3)设置船体为固壁边界条件。

4)其它边界设置为对称面,满足对称条件。

3 数值计算

本文在数值计算时使用有限体积离散控制方程,湍流模式选择了RNG k-ε模型,对流项采用二阶迎风差分格式,扩散项采用中心差分格式,采用非定常分步隐式格式,求解离散的代数方程使用SIMPLEC方法求解。

单船计算区域的网格划分原则是：靠近船体较密,远离船体较疏,艏艉密,中部疏。由于船体的对称性,只模拟半船,流体区域只取一半,这样可以减少网格,提高计算速度。网格总数约32万,如图1所示。

两船计算区域的网格划分原则是：两船从艏艉到中部由密到疏,从艏艉到进出口边界也是由密到疏,两船外侧距船越远越疏,内侧也是,但是内侧网格较密,因为是计算的主要区域。由于两船的型值一样,并且整个流体区域也是对称的,为了节约计算时间,因此只画了半个流场,运用对称性质,计算结果不受影响。网格总数约37万,如图2所示。

图1 单船网格划分

图2 两船网格划分

4 计算结果及分析

1)阻力分析

阻力计算结果如表1所示,从表1可以看出,由于两船的干扰,两船的总阻力比单船的两倍阻力大,并且总阻力随着两船间距的增大而减小,随着船速的增大而增大,并且两船在高速状态下阻力增加比较明显,最高可达27.3%。说明两船的间距越小,航速越大,两船的干扰作用就越大。

表1 总阻力比较

2)波形和波高分析

首先我们通过Fluent软件自带的图像生成功能,截取几个不同状态下的波形图,方便我们直观的了解和分析,波形图3～图5所示。

从3个图中可以看出,图2和图3两船之间的干扰明显比图1中的激烈,这就说明了相同速度下间距越小的两船干扰越大,相同间距下速度越大的两船干扰越大。

这个结论与我们做的模型试验现象是一致的。

图3 间距1.5 m,速度1.138 7 m/s

图4 间距1.2 m,速度1.138 7 m/s

图5 间距1.5 m,速度1.626 7 m/s

下面取两船干扰时中间对称面处的波形进行比较,因为我们在武汉理工大学做的模型试验主要是采用浪高仪测量两船中间的波高,所以我们将比较一下各个状态的波形参数。

波高比较：从图6中可以得出,单船在低速航行时艏部的兴波是最大的,沿着船长方向波是在衰减的,但是在艉部,由于船型的特殊性兴波会有所增大,除艏部以外,第一个波峰是在距离船首1 m左右的地方,最大峰值在0.003 5 m左右,随着横向间距的增大,波的衰减比较厉害,峰值降到0.000 7 m左右,峰值出现的地方随着间距的增大向船尾方向移动,沿着整个船长出现3～4个波。

从图7中可以得出,艏部在兴波的作用下,波高值与单船的波高值大小是差不多的,但是由于两船的干扰作用,中间对称面的波是比较激烈的,并且速度越大干扰越大。第一个峰值也是出现在距离船首1 m左右的地方,并且随着两船间距的增大峰值点在向船尾方向移动,峰值最大的在0.007 m左右,最小的在0.003 m左右,是单船兴波的2～3倍,沿着船长方向也是会出现3～4个波,与我们在武汉理工大学水池的试验对比,波形比较一致,相位也比较一致,但是波峰波谷有差异,因为静水兴波值本身就不大,船型也不一致,主要因为艏部线型相差较大,对兴波的差异就大,并且实验时有干扰,所以导致数值上的差异,但是可以证明数值计算是可行的。

图6 速度1.138 7 m/s时的单船相应间距的波形图

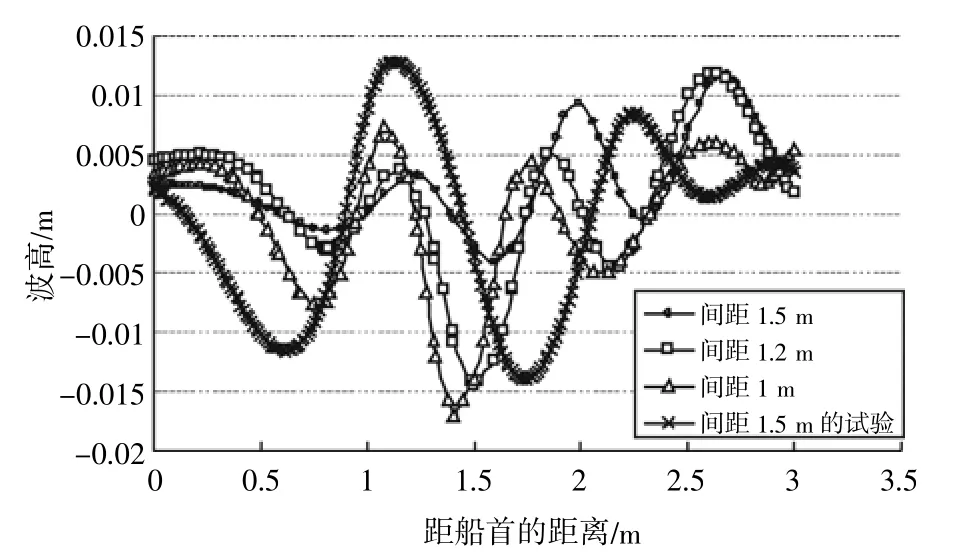
图7 速度1.138 7 m/s时的两船对称面的波形图

从图8中我们可以看出,由于航速的增大,相对于图6的低速来说,整个波形的相位是向船尾方向移动的,峰值点是出现在距离船首2 m左右的位置,并且随着间距的增大向船尾方向移动,峰值最大可以达到0.011 m左右,最小在0.008 m左右,比图6的兴波大很多,说明航速的增大对兴波的影响时比较大的,沿着整个船长方向出现2个波。

图8 速度1.626 7 m/s时的单船相应间距的波形图

从图9中可以看出,同样是由于航速的增大,整个沿船长方向的波形相位是向船尾方向移动的,由于两船的兴波干扰作用,波峰与波谷的绝对值都很大,可以看到,波峰的值上升到了0.04 m左右,接近单船干扰的4倍,峰值点也是出现在2 m左右的位置,并且随着两船间距的增大向船尾方向移动,沿着整个船长方向出现2个波。同样与我们在武汉理工大学的水池实验进行对比,波形趋势峰值大小基本是一致的,由于航速的增大,导致兴波的增大,由外界的因素造成的误差会相对较小,因此比低航速的更加靠近理论计算,但是由于船型的不一致,差异还是存在的。

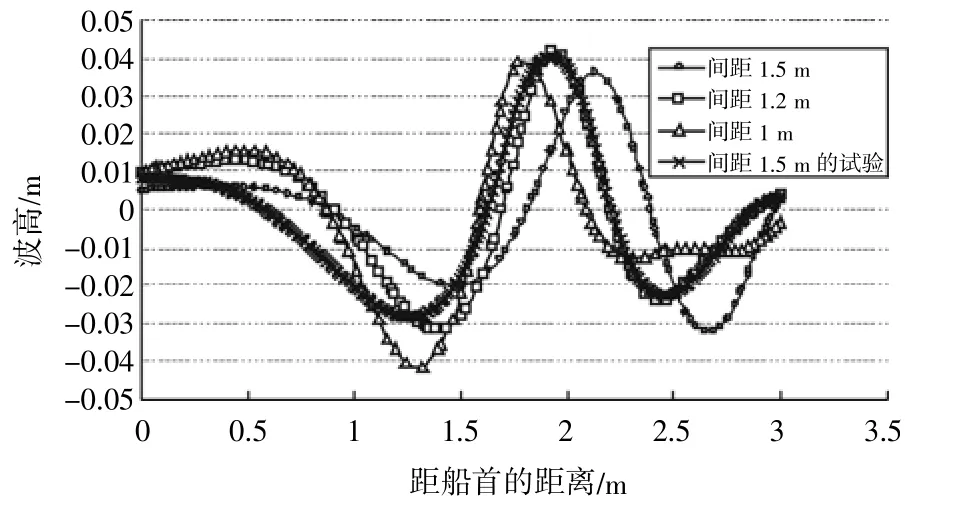
图9 速度1.626 7 m/s时的两船对称面的波形图

从上面的比较来看,速度和两船间距是两船的兴波干扰大小很重要的因素,对比可以看出,高速小间距的兴波可以达到低速大间距兴波的10倍以上。我们可以得出结论,航速是导致波形相位移动的主要因素,间距的减小和航速的增大是导致两船干扰波的大小的主要因素。这个跟我们在实验中观察到的现象是一致的,因为船型不一样,下一步将进行实验模型的数值模拟。

3)船体压力分布

船体的压力分布情况如图10～图12所示。

从图10～图12中可以看出,航速相同时,间距越小,船体所受的表面压力就越大；间距相同时,航速越大,船体所受的表面压力就越大。压力最大值出现在船首和船尾,并且值的大小也是符合实际情况的。

本文没有考虑升沉纵倾的因素是因为在静水中低速情况下,升沉纵倾很小,可以忽略。

可以从图13看出,Fr在0.2～0.3时,两条曲线相差不大,所以升沉纵倾可以忽略不计。

图11 速度1.626 7 m/s间距1.5 m时两船表面压力分布图

图12 速度1.138 7 m/s间距1.5 m时两船表面压力分布图

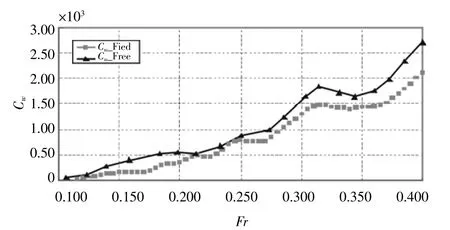
图13 Wigley船型实验数据

5 结论

模拟计算的结果与我们实验观测到的现象是一致的,说明运用计算流体力学软件Fluent进行模拟计算是可行的,从计算结果我们得到,间距和速度对两船的静水兴波干扰阻力和波形的影响规律：

1)两船横向间距越小,船速越大会增大两船的兴波,并且总阻力也会增大；

2)低速时第一个波峰出现在1 m左右的位置,高速时出现在2 m左右的位置,说明航速是改变波形相位的主要因素；

3)间距增大时,无论低高速第一个波峰的位置会向船尾方向移动,说明间距也是改变波形相位的一个因素；

4)高航速小间距时兴波的波峰最大,可达低速大间距的10倍,说明航速和间距的共同作用是影响兴波干扰的主要因素。

5)航速相同时,间距越小,船体所受的表面压力就越大；间距相同时,航速越大,船体所受的表面压力就越大。

因此在补给时要避免在兴波大的地方补给,把补给点选在尽量平缓的地方,这样可以确保补给安全进行。没有考虑到两船的横向移动是本次计算模拟的不足之处,由于我们实验时,是在水池中利用拖车来进行,两船在导航杆的作用下横向运动也被约束了,因此本次计算没有考虑到横向作用力的问题,这将在下一步进行研究。由于模拟的是Wigley船型,与试验船型有所不同,本次计算目的在于验证模拟的可行性,下一步将模拟我们试验的船型,并且与试验得到的数据加以比较,进一步研究两排水量相当的船型在静水中的兴波干扰影响。

［1］ OHKUSU M.On the heaving motion of two circular cylinders on the surface of a fluid［R］.Reports of the Research Institute of Applied Mechanics,Kyushu University,1969.

［2］ Van OORTMERSSEN G.Hydrodynamic interaction between two structures floating in waves［C］//Proceedings of Boss'77,1979.

［3］ KODAN N.The motions of adjacent floating structures in oblique waves［C］//3rd International Symposium on Offshore Mechanics and Arctic Engineering,1984.

［4］ LOKEN A E.Hydrodynamic interaction between several floating bodies of arbitrary form in waves［C］//International Symposium on Hydrodynamics in Ocean Engineering, 1981.

［5］ DUNCAN J H,BARR R A,LIU Y Z.Computations of the coupled response of two bodies in a seaway［C］//International Workshop on Ship and Platform Motions,1983.

［6］ KORSMEYER F T,LEE C H,NEWMAN J N.Computation of ship interaction forces in restricted waves［J］.Journal of Ship Research,1993,37(4)：298-306.

［7］ WILLIAMS A N,RANGAPPA T.Approximate hydrodynamic analysis of multi-column ocean structures［J］.Ocean Eng,1994,21(6)：519-573.

［8］ ZHANG X T,TENG B,ZHANG L W,et al.Numerical calculation for hydrodynamics of 3-D ship Hull based on B-spline［J］.Journal of Ship Mechanics,2002,6(6)：28-37.

［9］ 王建方.舰/舰补给系统中水动力学问题的数值仿真研究［D］.哈尔滨：哈尔滨工程大学.2005

［10］刘志华,董文才.V型沟槽尖峰形状对减阻效果及流场特性影响的数值分析 ［J］.水动力学研究与进展,2006, 21(2)：223-231.

Numerical Simulation of Wave-Making Interactions Between Two Ships in Calm Water

Wang Xiao-long Bi Yi
College of Naval Architecture and Power,Naval University of Engineering,Wuhan 430033,China

Numerical simulation on wave-making interactions between two ships with similar displacement was carried out by the VOF method.Two Wigley ships with the same form were used,and RNG k-ε model turbulent flow model was employed in the calculation.Different spacing and speed were investigated in the simulation to obtain the wave height distribution and the maximum wave height positions between two ships.The maximum wave height emerges at one-third length of the ship at low speed and two-third length at relatively high speed.This result is in accordance with the model test data which proves the availability of the calculation method.More complicated simulation of the interactions between two ships can be built on this method.

VOF method；Wigley ship；free surface；wave-making interaction

U661.1

A

1673-3185(2010)06-60-05

10.3969/j.issn.1673-3185.2010.06.012

2010-05-11

王小龙(1986-),男,硕士研究生。研究方向：流体力学。E-mail：hailong128@gmail.com

毕 毅(1963-),男,副教授,硕士生导师。研究方向：船舶流体力学