考虑可压缩性及惯性力的油膜力研究

姚熊亮张 成孙士丽

1哈尔滨工程大学船舶工程学院,黑龙江哈尔滨150001

2哈尔滨工程大学机电工程学院,黑龙江哈尔滨150001

考虑可压缩性及惯性力的油膜力研究

姚熊亮1张 成2孙士丽1

1哈尔滨工程大学船舶工程学院,黑龙江哈尔滨150001

2哈尔滨工程大学机电工程学院,黑龙江哈尔滨150001

一般油膜压力特性研究都是基于流体不可压缩的假设,没有计及可压缩性以及轴颈惯性力对油膜压力的影响,但在瞬态冲击重载作用下,油膜压力随时间变化剧烈,而油膜密度、粘度等状态参数又是关于压力的函数,此时,油膜不可压缩性假设不再适用。另外,冲击载荷作用下轴颈本身存在很高的加速度,因轴颈高速运动而产生的惯性力也不能被忽略。可压缩性以及轴颈惯性力引入到油膜压力的数值计算,使计算结果更符合实际的物理现象。

油膜压力；可压缩性；惯性力；瞬态冲击

1 引言

滑动轴承的油膜不仅起着承受载荷,减轻摩擦,消除磨损的作用,从动力学观点来看,它也是转子—支撑—基础这个系统中的一个环节。油膜的特性,对整个转子系统的动力形态有很大影响。油膜的动态特性会影响转子系统的临界转速、振幅及稳定性等［1］。研究油膜的动态特性主要是基于对雷诺方程的求解,以往求解雷诺方程时,一般假设流体的物态参数密度和粘度为常数。这个假设在轴承承受的载荷变化缓和时其计算结果是合理的,但当轴承承受瞬态冲击载荷时,油膜的压力变化是剧烈的,而油膜密度和粘度是随着压力变化的,这时假设密度和粘度是常数不再合理。并且传统计算油膜压力分布时基本不考虑轴颈惯性力的影响,但是在冲击载荷作用下轴颈本身具有很高的加速度,此时研究油膜力的分布必须考虑轴颈惯性力的影响。本文建立了考虑轴颈惯性力的力平衡方程以及考虑油膜可压缩性的雷诺方程,计算轴承在瞬态冲击载荷,如矩形脉冲、三角形脉冲以及正弦周期性载荷等作用下的油膜压力特性,分析数值计算结果,研究外载荷幅值、脉宽以及相对间隙对油膜动态特性的影响。

2 油膜状态参数对油膜力特性的影响

本文主要考虑在高频动载工况下油膜力的变化情况,在高频动载工况下油膜力变化剧烈,求解油膜压力必须考虑润滑油的状态参数变化对油膜压力的影响。

计算动载荷作用下轴承内油膜压力的传统方法是求解雷诺方程,雷诺方程形式如下［2］。

式中,p为油膜压力；h为油膜厚度；x为周向位移；z为轴向位移；U1为轴颈线位移；U2为轴承线位移；V0为轴心速度。

使用该方程对油膜压力进行计算时,没有考虑到密度ρ和粘度η随压力变化,这是因为在一般动载荷作用下,油膜压力随时间变化缓和,因此,可以忽略油膜压力变化对密度ρ和粘度η的影响。假定密度ρ和粘度η为常数。

但在高频载荷(如冲击载荷)作用下,油膜压力随时间变化剧烈,油膜状态参数如密度ρ和粘度η会因油膜压力的剧烈变化而发生显著变化。因此对高频载荷作用下油膜压力计算,本文认为应该考虑密度ρ和粘度η随压力变化的特征。考虑这一特征的雷诺方程形式为［3-4］：

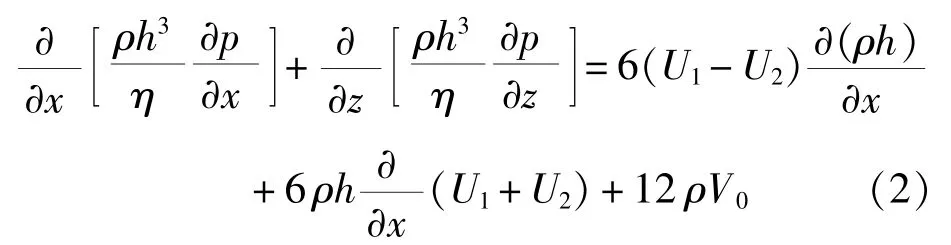
在等温条件下,适用于高频载荷工况下的润滑剂的密度方程可由式(3)表示［5］,粘度方程可由式(4)表示［6］。

润滑剂的密度方程采用Dowson-Higginson公式：

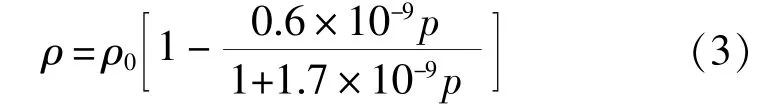
式中,ρ0为压力为零时的密度,与温度有关,因为本文仅研究等温变化,因此ρ0为常数；p为油膜压力,Pa。

润滑剂的粘度方程采用Roelands公式：

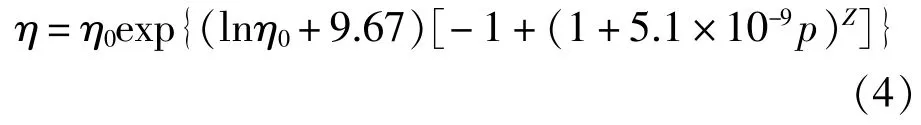
式中,η0是压力为0,温度为T0时的动力粘度；p为油膜压力,Pa；Z为Roelands系数,取Z=0.6。

3 计入密度、粘度变化的油膜力特性计算

计入式(3)、式(4)后的雷诺方程为式(2),求解该方程即可得出考虑密度和粘度随压力变化时动特性的变化情况。本文在考虑油膜状态参数随压力变化的基础上,对各种形态载荷包括不规则载荷、正弦周期载荷作用下的油膜力进行重新计算,研究油膜状态参数密度ρ和粘度η对油膜动态特性的影响。现计算在高频动载荷作用下轴承油膜压力最大值随时间变化情况、轴承偏心率和偏位角随时间变化情况。例如,冲载荷作用下轴承受力时历曲线如图1所示。

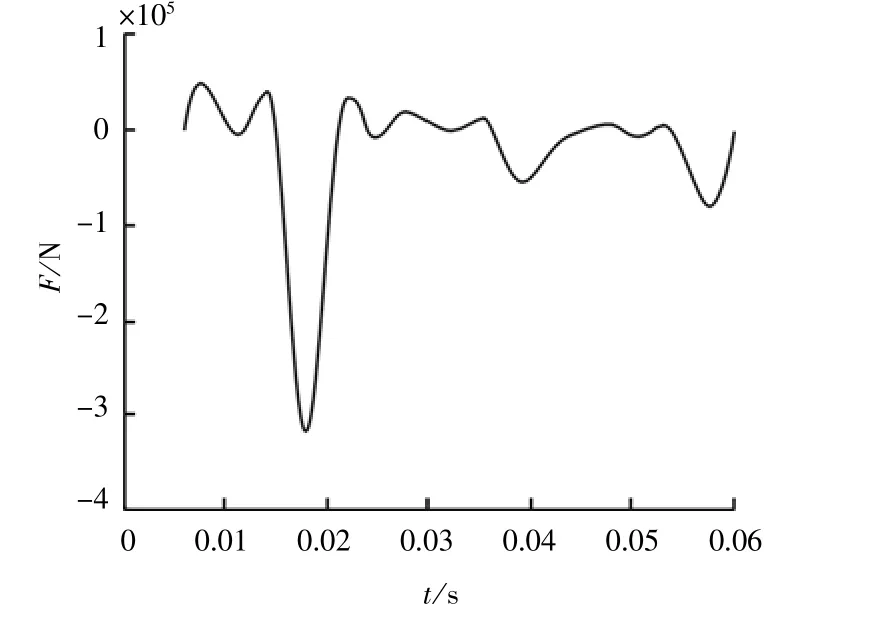
图1 载荷时历曲线

在上述载荷作用下,最小油膜厚度处油膜压力随时间变化曲线如图2所示。

图2 a 不考虑参数变化和考虑参数变化时油膜力时历曲线

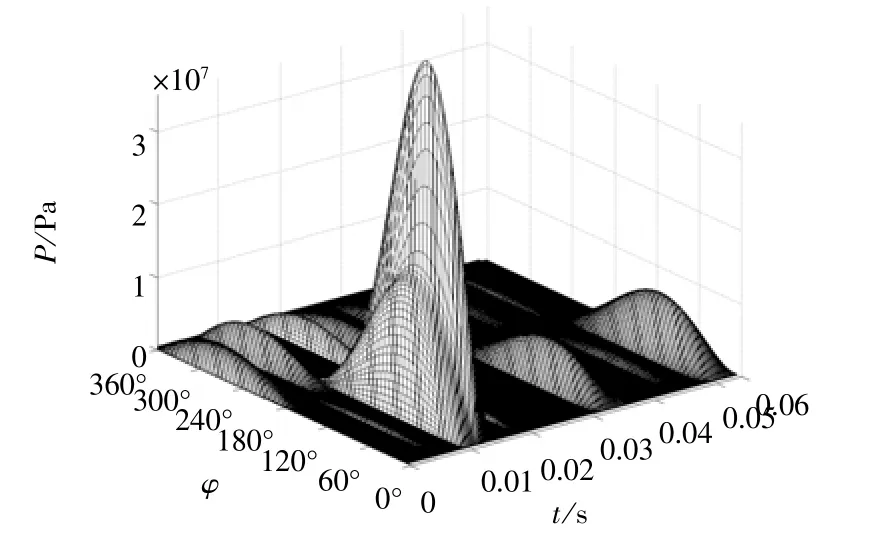
图2 b 考虑参数变化时最小油膜厚度截面处油膜力三维变化情况

图2a中虚线为不考虑油膜密度ρ和粘度η随压力变化时油膜力变化情况,实线为考虑油膜密度ρ和粘度η随压力变化时油膜力变化情况。可以看出在冲击载荷作用下油膜状态参数随压力的变化对油膜压力影响显著,两种情况下油膜压力波形一致,但在重载作用时段计入状态参数变化后的油膜压力峰值明显增大。图2b为考虑参数变化时最小油膜厚度所在截面处油膜压力随时间变化情况。

图3为在冲击载荷作用下轴颈偏位角φ和偏心率e的时历曲线,虚线不考虑油膜密度ρ和粘度η的变化,实线为考虑油膜密度ρ和粘度η随压力变化时的情况。可以看出在该载荷的作用下,其中偏心率的变化较偏位角变化明显。因为偏位角主要受外载荷的方位角的影响,而在相同载荷作用下偏心率更为明显地反映了油膜的承载能力,考虑压力影响时油膜粘度η是增大的。虽然密度随压力增大是减小的,但观察式(2)可以知道其对压力分布影响很小,所以受粘度增大的影响油膜的承载能力是增大的,所以偏心率随参数的变化较偏位角变化明显。

考虑周期性载荷作用下轴承内油膜的动态性能。载荷幅值为3×105N,载荷频率为100 Hz,作用方向为垂向。载荷时历曲线如图4所示。

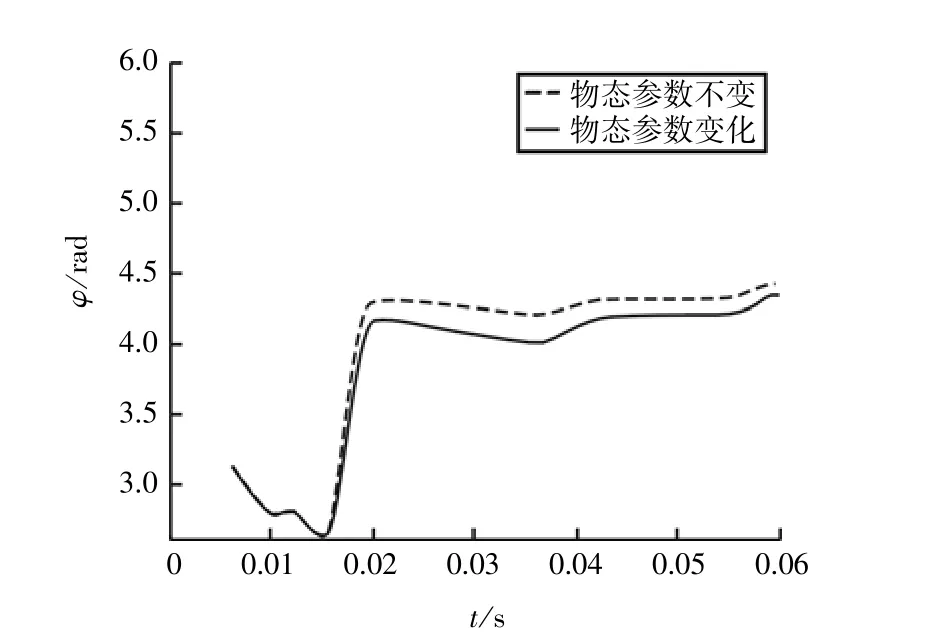
图3 a 不考虑参数变化和考虑参数变化时偏位角时历曲线

图3 b 不考虑参数变化和考虑参数变化时偏心率时历曲线

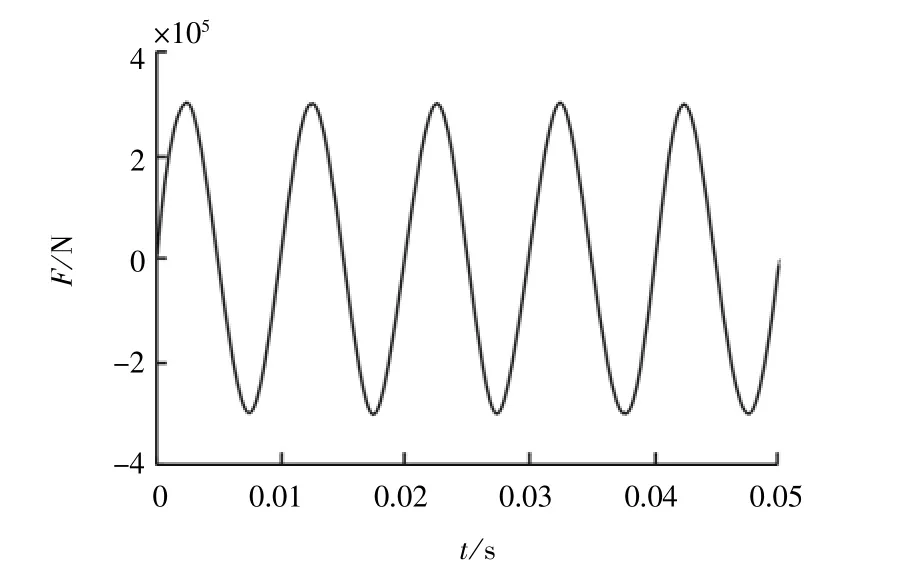
图4 正弦周期载荷时历曲线

在上述正弦周期载荷作用下,最小油膜厚度处油膜压力随时间变化情况如图5所示。

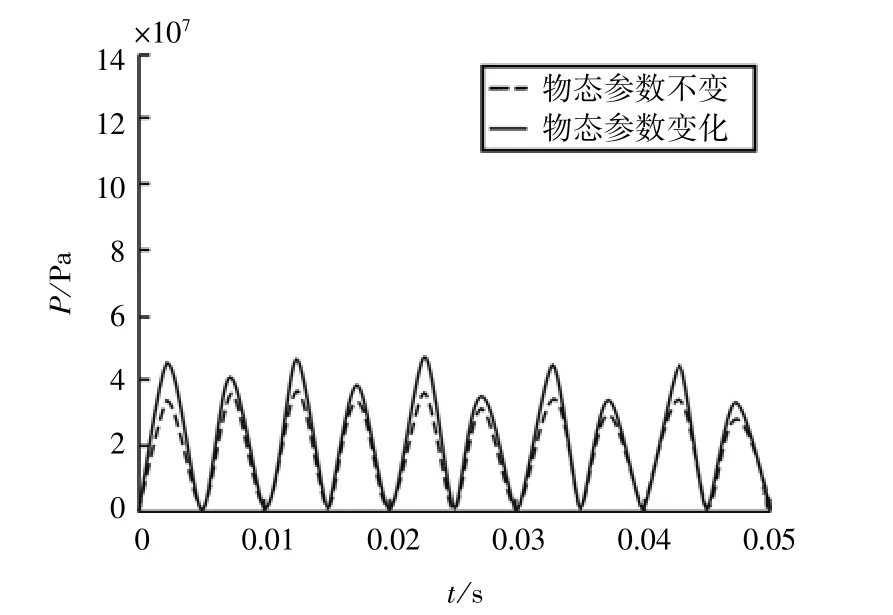
图5 a 不考虑参数变化和考虑参数变化时油膜力时历曲线

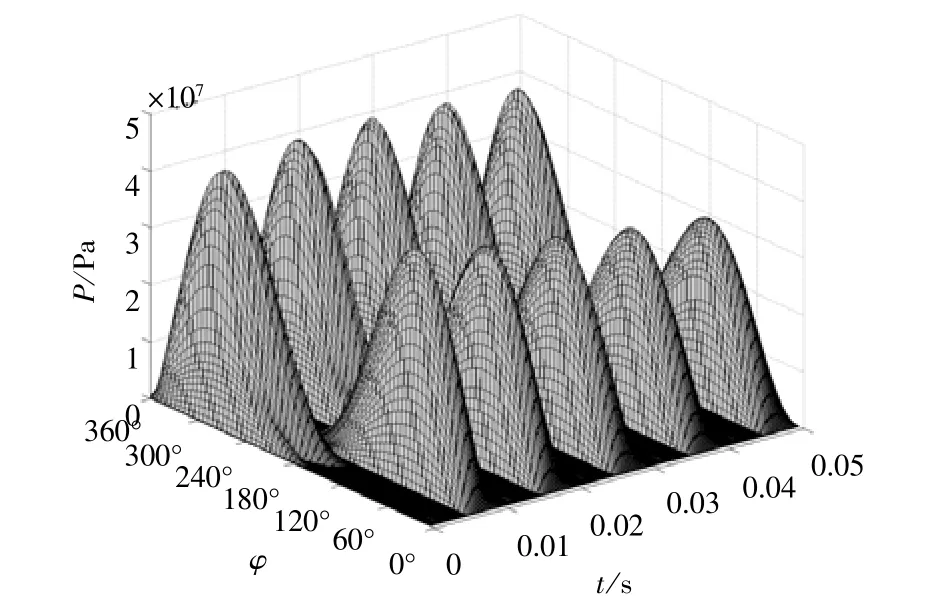
图5 b 考虑参数变化时最小油膜厚度截面处油膜力三维变化情况

图5a中虚线为不考虑油膜密度ρ和粘度η随压力变化时油膜力变化情况,实线为考虑油膜密度ρ和粘度η随压力变化时油膜力变化情况。由图可知,在油膜压力小于一定界限值时,如小于20 MPa时油膜压力曲线和不考虑密度ρ和粘度η变化情况下的压力曲线一致,表示在油膜压力小于20 MPa时密度ρ和粘度η变化不大。而当压力超过该界限值时,密度ρ和粘度η变化明显,其对压力也产生明显影响,使得油膜压力峰值明显增大。由此可知,油膜压力很大时密度ρ和粘度η的变化对油膜压力的影响是不能忽略的。图5b为考虑参数变化时最小油膜厚度所在截面处油膜压力随时间变化情况。

图6a和图6b分别为在周期载荷作用下轴颈偏位角φ和偏心率e的时历曲线,其中虚线为不考虑油膜密度ρ和粘度η随压力变化时情况,实线为考虑油膜密度ρ和粘度η随压力变化时情况。在任意载荷作用下油膜动态特性的一些特点在正弦周期载荷情况下仍能反映出来,如偏位角受密度ρ和粘度η的影响比较小,而偏心率受影响比较大。偏位角时历曲线只是在局部峰值处发生变化,而偏心率时历曲线则整体发生偏移。产生这一差异的原因主要是,偏位角主要受外载荷影响,而偏心率不仅受外载荷影响还与油膜承载能力有很大关系。结合偏心率时历曲线可以知道,当考虑密度ρ和粘度η随压力变化时油膜承载能力增强。

计算出各种载荷作用下油膜偏位角φ和偏心率e后即可得出轴心轨迹随时间变化情况,如图7所示。

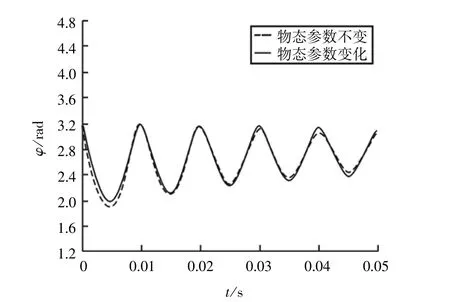
图6 a 不考虑参数变化和考虑参数变化时偏位角时历曲线

图6 b 不考虑参数变化和考虑参数变化时偏心率时历曲线

4 轴颈惯性力对油膜力特性的影响

本文将对可压缩雷诺方程求解,经化简,可得下式［1-2］。

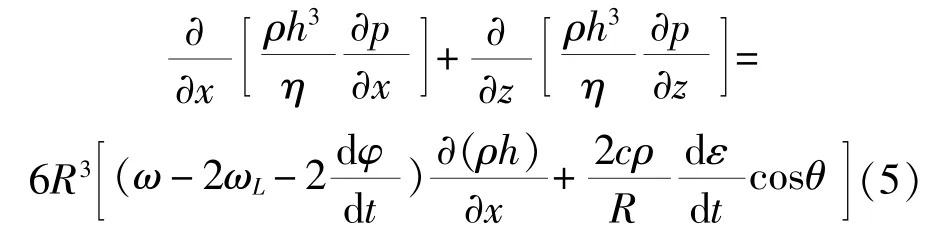
式中,ω为轴颈自转角速度；ωL动载荷旋转角速度；φ为偏位角；ε为偏心率；c为绝对间隙。

图7 a 冲击载荷作用下轴心轨迹时历曲线

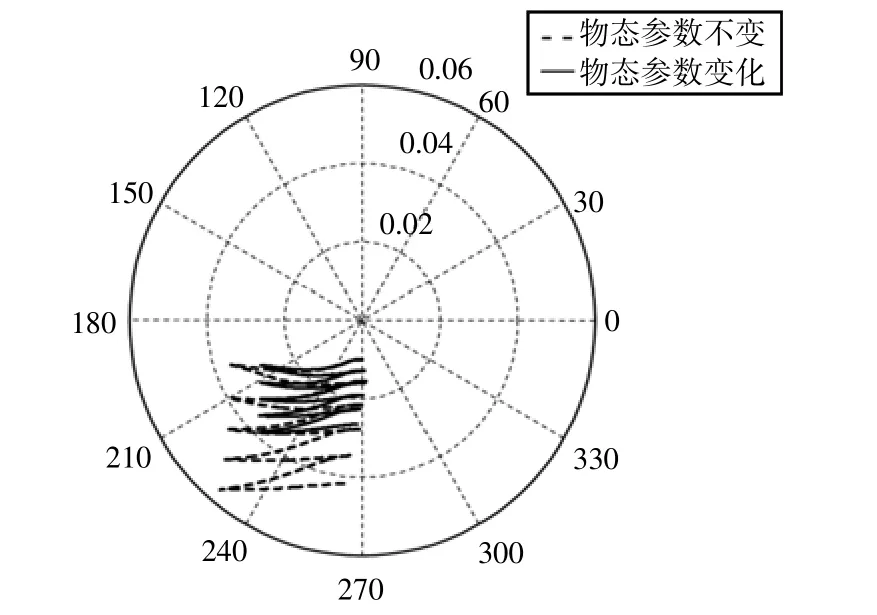
图7 b 正弦周期载荷作用下轴心轨迹时历曲线

图8中,x'指向最小油膜厚度方向；y'与x'垂直,为随时间变化的动坐标系；x、y为不随时间变化的定坐标系；e为偏心距离；R'为轴承半径；R为轴颈半径；I为轴颈惯性力；W为油膜力合力；F为外载荷。

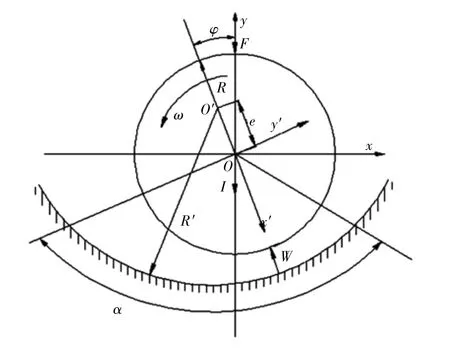
图8 径向滑动轴承几何参数

将式(5)无量纲化,无量纲因子为：

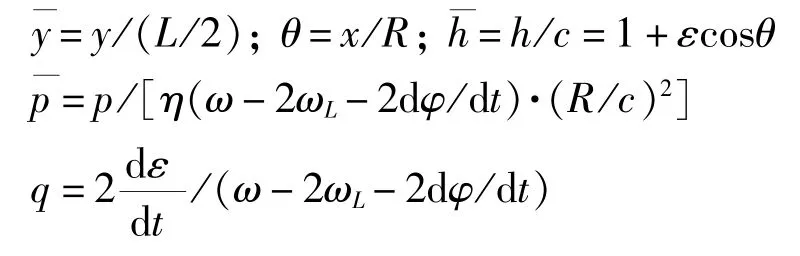
得式(6)：

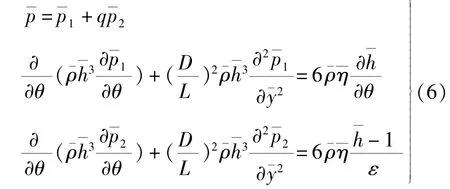
该式对应的边界条件为：

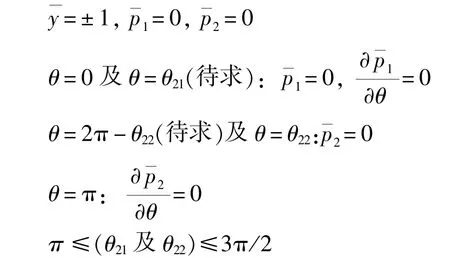
采用超松弛迭代法对上式进行计算,从而得合成油膜p(θ)的承载能力为：

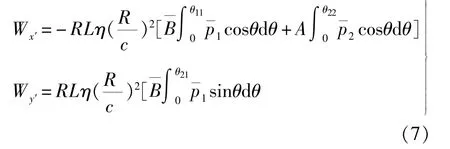
应该指出的是,求解油膜力的传统力平衡方程为外载荷与油膜力平衡,即W=G,没有考虑到惯性力的作用。但在瞬态冲击载荷作用下,轴颈运动剧烈,产生的惯性力也较大。因此,在瞬态冲击载荷作用下,必须考虑轴颈惯性力对油膜压力的影响。

F为直接作用于轴颈上的力,Fx和Fy分别为轴承两向负荷。

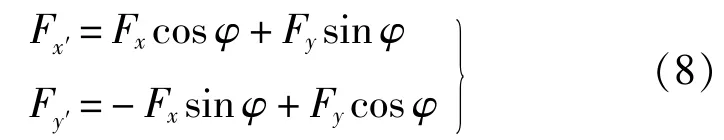
惯性力：

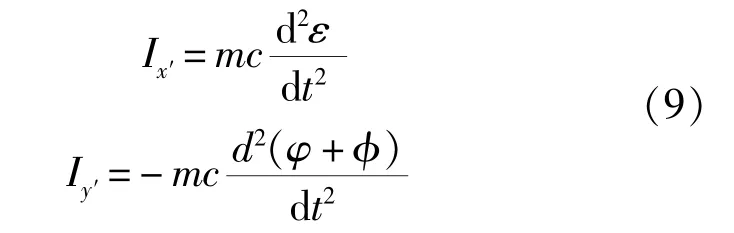
式中,m为轴颈质量；φ为外载荷方向与竖直参考线(y轴)间夹角。

根据力平衡方程：

得到关于偏心率ε和偏位角φ的偏微分方程：

联立方程式(5)和方程式(11)就可以得到在瞬态冲击载荷作用下轴承内油膜运动方程,用有限差分法解该方程,即可得对应时刻偏心率与偏位角。在给出初始值ε0,φ0后,逐点步进即得轴心轨迹。

5 考虑轴颈惯性力的油膜力特性计算

本文在考虑油膜可压缩性以及轴颈惯性力的基础上,对各种形态载荷包括矩形载荷以及正弦周期载荷作用下的油膜力进行重新计算,研究相对间隙c/R(c为轴承绝对间隙；R为轴承半径)对油膜动态特性的影响。例如,矩形脉冲载荷作用下油膜力变化趋势如图9所示,该矩形脉冲脉宽为0.01 s,脉冲幅值为10×103N,作用方向为垂向。本文中所有算例均取轴承直径为50 mm,轴长为30 mm,轴颈转速为16 m/s。

图9 矩形脉冲载荷时历曲线

在不考虑惯性力以及可压缩性的情况下,相对间隙对最小油膜厚度处油膜压力影响很小,如图10a所示,油膜压力随相对间隙的减小而稍有减小。在考虑可压缩性以及轴颈惯性力情况下,相对间隙的大小对油膜力变化趋势造成相当显著的影响,如图10b所示。可以从图10中观察到如下现象,首先由于惯性力的存在,在外载荷消失后,油膜力仍然存在；在外载荷消失的瞬间,油膜力有非常陡峭的增大,这是因为轴承在动载荷作用下油膜压力不仅和偏心位置有关,同时还受到偏心率变化率的影响,作用载荷有突变,导致偏心率变化率很大,因此油膜力存在陡峭增加；相对间隙对油膜力变化趋势影响很大,外载荷消失前,相对间隙越大,油膜力越小,外载荷消失后,相对间隙越大,油膜力越大,油膜压力衰减越缓慢,这说明相对间隙越大,惯性作用越不能忽略；从图10a中还可以看出,相对间隙极小的情况下,最小油膜厚度处油膜力时历曲线和不考虑惯性力以及可压缩性时油膜力时历曲线非常接近,并且相对间隙越小,油膜压力时历曲线越趋近于不考虑可压缩性时油膜力时历曲线,这也反映了油膜力变化关于相对间隙的渐进特性。

当载荷很高或脉宽不同时,油膜动态特性也可能会有变化,图11给出了矩形脉冲载荷作用下脉冲幅值A分别为1×103N,1×104N,5×104N, 1×105N时轴承最小油膜厚度处油膜力时历曲线,为了对不同幅值载荷作用下油膜压力进行比较,本文采用A/(2LR)对油膜压力进行无量纲化。图11b给出了矩形脉冲载荷作用下脉宽分别为0.01 s,0.015 s,0.2 s时轴承最小油膜厚度处油膜力时历曲线。

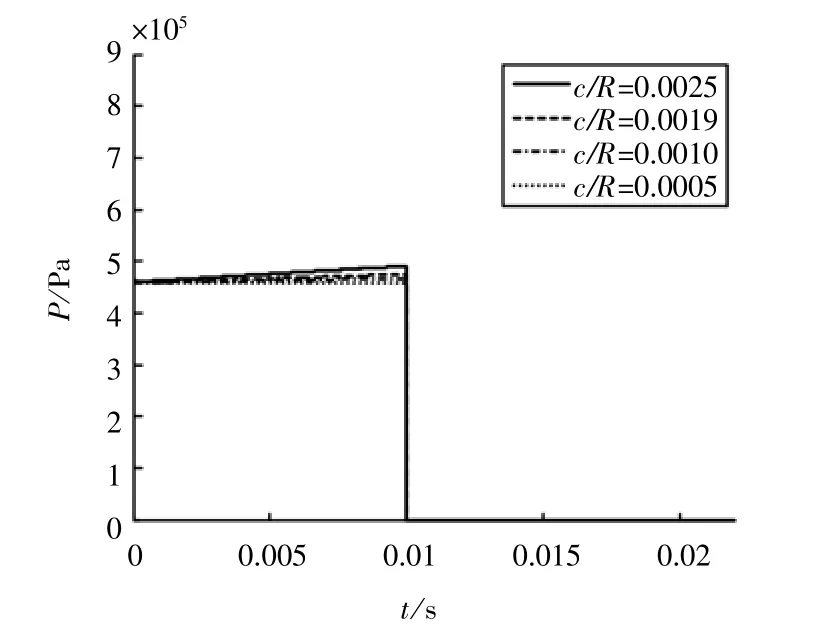
图10 a 不考虑惯性力及可压缩性时油膜力时历曲线

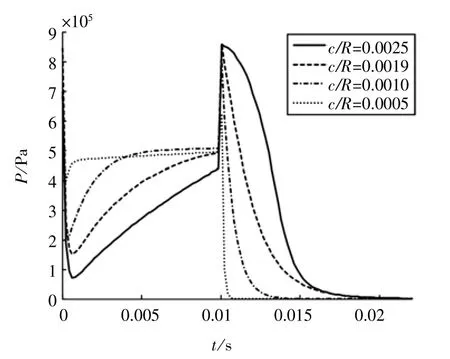
图10 b 考虑惯性力及可压缩性时油膜力时历曲线

图11 a 不同载荷幅值时无量纲油膜力时历曲线

图11 b 不同脉宽时无量纲油膜力时历曲线

当矩形脉冲幅值为1×104N或5×104N时,外载荷消失后,无量纲油膜力衰减较慢；矩形脉冲幅值为1×103N或1×105N时,外载荷消失后,油膜力衰减较快；这就意味着无量纲油膜力衰减速度并不随外载荷单调变化,外载荷极小,或外载荷极大,油膜力衰减速度均较快。另外,无论是冲击前还是冲击后,外载荷幅值对无量纲油膜力变化趋势均有显著影响。脉宽变化对无量纲油膜力衰减速度影响不大。

考虑周期性载荷作用下轴承内油膜的动态性能 (图12)。载荷幅值为1×104N,载荷频率为100 Hz,作用方向为垂向。

观察图13a可以知道所加外载虽然是幅值相等的周期性载荷,但在不考虑可压缩性以及轴颈惯性力情况下,每一条油膜力时历曲线上都会出现局部峰值,相对间隙越小,局部峰值出现时刻越早,数值越大。为了对油膜力的振动特性做进一步研究,对c/R=0.001时油膜力时历曲线做进一步计算,延长其计算时间到0.12 s。

由图13b中可以看出,轴颈虽然在外载荷作用下做受迫振动,但是油膜力时历曲线明显还存在另一种周期性规律。当激振力频率ωj和系统固有频率ωn相当接近,但它们并不相等时,会发生一种现象,即系统的振幅时而增大,时而减小,该现象即为拍振现象。拍的振幅变化频率Δ的计算公式为Δ=(ωj-ωn)/2,Δ为很小的一个值,振幅变化周期π/Δ是一个大值。在本算例中,振幅变化周期π/Δ大概为0.058 s,振幅变化频率大概是17.24 Hz,外界激励力频率是100 Hz,那么系统固有频率为82.76 Hz。该拍振现象产生的原因可能是因为在考虑轴颈惯性力情况下,轴颈、油膜、轴承组成一振动系统,该振动系统本身也存在固有频率,当该固有频率和外界激励力频率接近时,就会在油膜力时历曲线上观察到拍振现象。

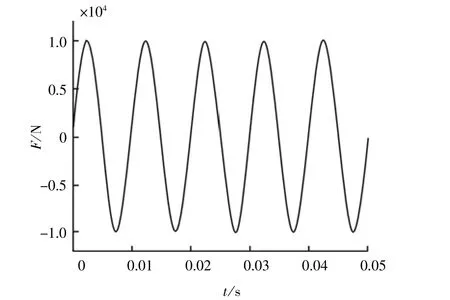
图12 正弦周期载荷时历曲线

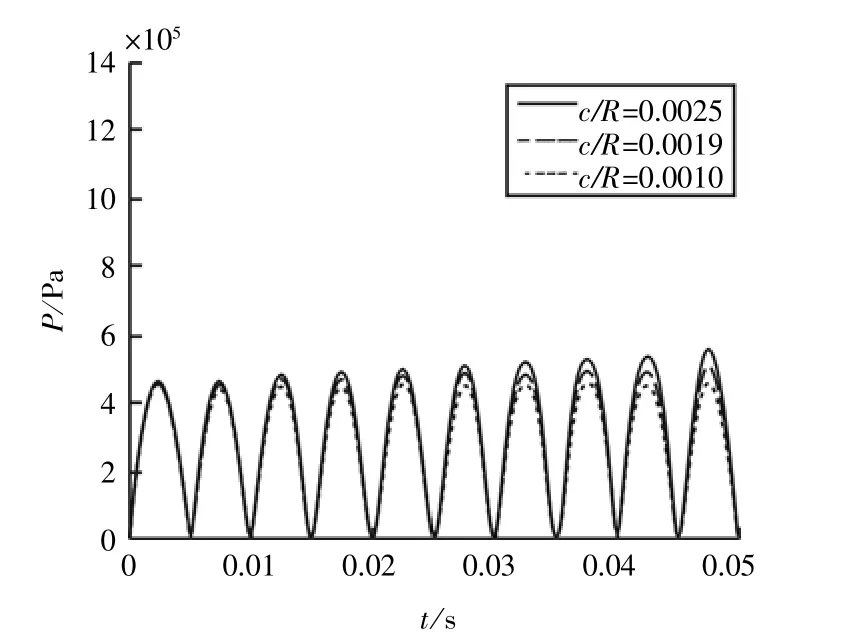
图13 a 不考虑惯性力及可压缩性时油膜力时历曲线

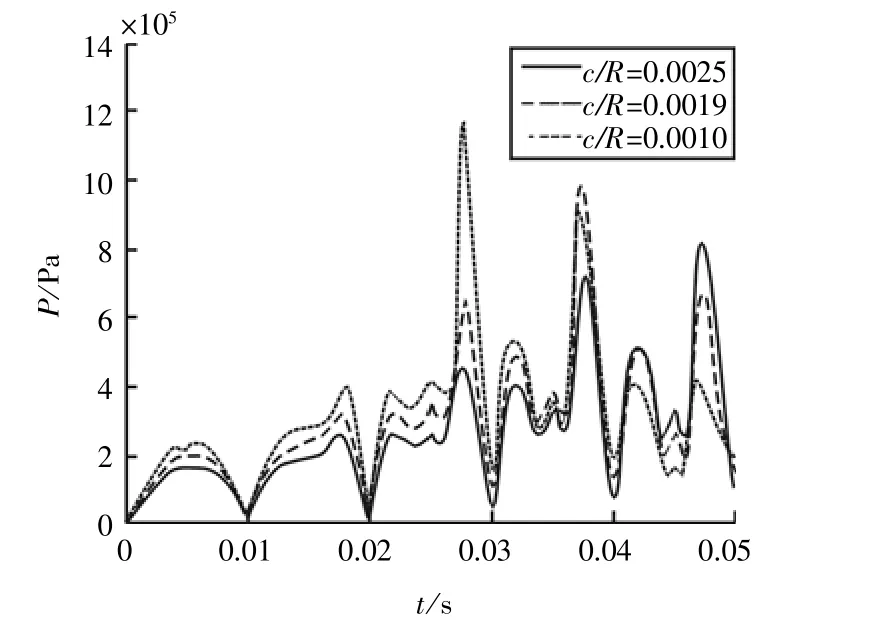
图13 b 考虑惯性力以及可压缩性时油膜力时历曲线

图14 a 不考虑惯性力以及可压缩性时油膜力时历曲线

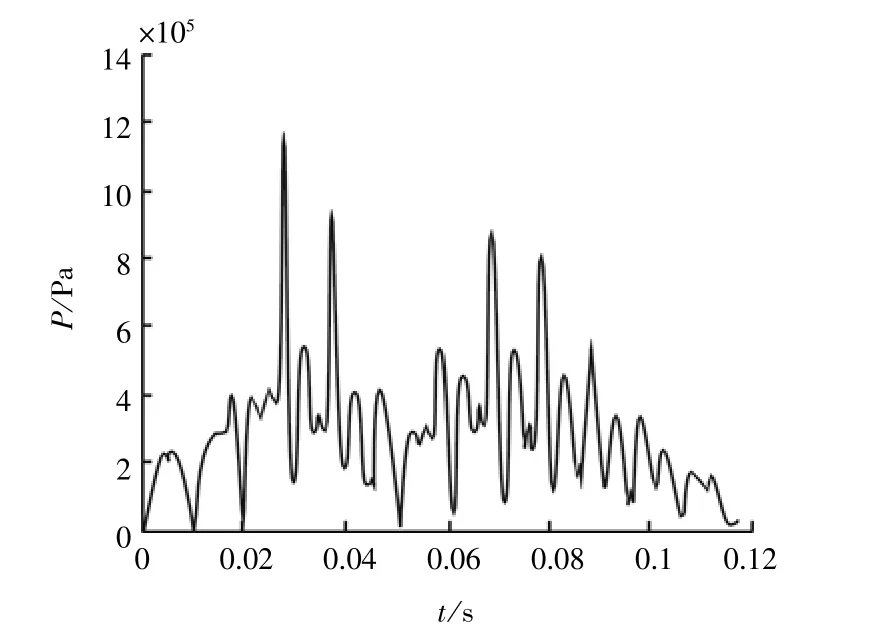
图14 b 考虑惯性力以及可压缩性时油膜力时历曲线

6 油膜静刚度精度验证

油膜对转子动态特性起主要作用的因素是径向刚度,周向刚度很小,可以忽略。本文采用超松弛迭代法对液体静压雷诺方程进行计算,从而得到油膜静刚度,并将该数值计算结果与文献［7］实验结果进行对比,从而验证该程序的正确性。取轴承直径为50 mm,轴长为30 mm,相对间隙为0.12%。油膜静刚度数值计算结果与试验结果对比曲线如图15所示,横坐标为无量纲载荷,无量纲静载荷Se=Fe/Ce,Fe为油膜在处于平衡状态情况下所承受的静载载荷,无量纲因子Ce为(c/R)2/ (η0ωRL),纵坐标为无量纲油膜刚度,水平方向无量纲油膜刚度Kxx=Kx/Ke,Kx为水平方向油膜静刚度；垂向无量纲油膜刚度Kyy=Ky/Ke,Ky为垂向油膜静刚度；无量纲因子为Ke=η0ωL/(c/R)3。

由图15可知,无量纲油膜刚度随无量纲静载荷S增大而增大。数值解和实验解变化趋势大致相同,某些点数值解和实验解差异较大,但总的来说,数值解和实验解吻合很好。

7 结论

本文建立了考虑轴颈惯性力的力平衡方程以及考虑油膜可压缩性的雷诺方程,计算轴承在瞬态冲击载荷如矩形脉冲、三角形脉冲以及正弦周期性载荷作用下的油膜力时历曲线,以及偏心率、偏位角时历曲线。通过对计算数据的分析,得到结论如下。

图15 b Kyy随Se变化曲线

图15 c Kxy随Se变化曲线

图15 d Kyx随Se变化曲线

1)当油膜压力达到107量级时油膜密度和粘度变化对油膜力影响显著,使油膜力在峰值区域明显增大。

2)相对间隙对油膜力变化趋势影响很大,外载荷消失前,相对间隙越大,油膜力越小,外载荷消失后,油膜力仍然存在,相对间隙越大,油膜力越大,油膜压力衰减越缓慢,这说明相对间隙越大,轴颈惯性作用越不能被忽略。在考虑可压缩性以及轴颈惯性力情况下,油膜力时历曲线上会出现局部峰值,相对间隙越小,局部峰值出现时刻越早,峰值越大。

3)无量纲油膜力衰减速度并不随外载荷幅值单调变化,外载荷幅值极小,或外载荷幅值极大,无量纲油膜力衰减速度均较快。脉宽变化对无量纲油膜力衰减速度影响不大。

4)考虑可压缩性以及轴颈惯性力情况下,可能会在油膜力时历曲线上出现拍振现象。

本文所采用的计算方程均来自基本的计算公式的推导,虽然本文主要考虑极端情况下的油膜的压力分布情况,但本文的计算模型仍然适用于一般工况下油膜压力的计算,只是本文中所体现的各种现象不会太明显。

［1］ 钟一谔,何衍宗,王正,等.转子动力学［M］.北京：清华大学出版社,1987.

［2］ 池长青.流体力学润滑［M］.北京：国防工业出版社,1998.

［3］ 曹树谦,丁千,陈予恕,等.具有滑动轴承的稳态转子系统有限元建模分析［J］.汽轮机技术,1999,41(6)：347-350,354.

［4］ 李晓彬,杜志鹏,夏利娟,等.考虑支撑动刚度的船舶轴系横向冲击响应计算［J］.振动与冲击,2006,25(2)：181-184.

［5］ 黄柏林,汪仁友,黄平,等.液体润滑油的密度研究［C］//第六届全国摩擦学学术会议论文集(下册),中国机械工程学会摩擦学分会,湖北,武汉,1997.

［6］ 刘莹,郭溪泉.高速重载径向滑动轴承热弹性计算方法的研究［J］.钢铁,1999,34(1)：57-62.

［7］ 戴学余,苗旭升,富彦丽,等.几种低粘度润滑介质下动静压轴承的性能分析［J］.润滑与密封,2004(3)：10-13, 17.

Analysis of Oil Film Force Considering Compressibility and Inertial Force

Yao Xiong-Liang1Zhang Cheng2Sun Shi-Li1
1 College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China
2 College of Mechanical and Electrical Engineering,Harbin Engineering University,Harbin 150001,China

The research on characteristics of oil film pressure was usually conducted based on the assumption of fluid incompressibility neglecting the impact of compressibility and the journal inertial force on oil film pressure.Oil film pressure however,will dramatically change with the varying time when subjected to transient shock heavy load,while density and viscosity of oil film are the function of oil pressure,thus the incompressibility assumption is no longer applicable in this case.Besides,the acceleration caused by shock loading exists in the journal and the inertial force of journal due to high motion of the journal cannot be neglected as well.Both the compressibility and the inertial force of journal were introduced in the calculation of oil film pressure to work out a result well agreed with practical one.

oil film pressure；compressibility；inertial force；transient shock

TH133.31

A

1673-3185(2010)06-33-08

10.3969/j.issn.1673-3185.2010.06.007

2009-09-15

姚熊亮(1963-),男,教授,博士生导师。研究方向：水下气泡动态特性研究、船舶结构动力学

张 成(1987-),男,硕士研究生。研究方向：机械强度设计。E-mail：zhangcheng1987530@163.com