MIKE21模型在涉河大桥防洪影响数值模拟中的应用

朱大伟,杨 侃,常蒲婷,沈雪娇

(河海大学 水文水资源与水利工程科学国家重点实验室,南京 210098)

新建铁路荆州至岳阳工程(简称荆岳铁路)位于鄂中南和湘东地区,线路起自湖北省荆州市,向南经湖北省的江陵、公安、石首以及湖南省的华容县等市县,终点至岳阳市。公安长江大桥是新建铁路荆州至岳阳工程跨越长江的特大铁路桥梁。根据水利部的有关规定,对于此类重要的大型涉水工程必须进行详尽的工程防洪影响计算。

目前对涉水工程的防洪影响评价分析手段主要是数学模型和物理模型两种技术手段。目前国际上已有不少成熟的平面二维水流模型商业软件,由丹麦水力研究所(DHI)研发的MIKE21平面二维水流模型是其中应用广泛的一款商业模型,在丹麦、澳大利亚、泰国及中国香港、台湾等国家及地区得到成功的应用。目前,该软件在我国也已成功应用于长江口综合整治[1]、太湖富营养化模型、杭州湾数值模拟等大型工程。本文通过使用MIKE21模型对荆岳大桥进行防洪影响数值模拟,并与同时开展的物理模型试验结果[2]进行对比分析。

1 基本方程和求解方法

1.1 基本方程

水流连续方程:

式中z为水位;p、q为x、y方向单宽流量;h为水深;s为源、汇项;six、siy分别为源 、汇项在 x、y 方向的分量;c为谢才阻力系数;Ω为科氏力;E为紊动扩散系数。

1.2 求解方法

计算区域采用矩形网格剖分,控制方程离散时,变量在矩形网格上采用交错布置,水位被定义在网格节点上,单宽流量被定义在各自方向的相邻网格节点的中部,见图1。数值计算方法采用交错方向隐格式算法(ADI)[3]。该算法的思路是对微分方程进行离散时,把每个时间步长分为 2个半步长,在前半步离散时,把对 x求导的项用隐式差分,对y求导的项采用显式差分,在后半个步长里则反之。

图1 交错网格布置Fig.1 Sketch of alternative grids

2 有关问题的处理

2.1 定解条件

初始条件包括初始水位和初始流速。初始水位和初始流速均设为常数,与实际值有误差,但是经过一段时间的计算后,在正确的边界条件控制下,误差会逐渐地消失。

边界条件为上游进口给定流量沿横断面的分布,下游出口给定水位。

2.2 糙率系数

模型糙率系数深槽部分取为0.017～0.025,边滩部分取为0.026～0.030,在局部高滩位置糙率取为0.031～0.033。

2.3 动边界处理系数

由于计算区域中存在随水位涨落而变化的动边界,为保证模型计算的连续性,采用“干湿处理技术”[4],当计算区域水深小于drying depth 0.02 m时,该计算区域的节点不参加计算,当水深大于flooding depth 0.02 m时,该计算区域的节点重新参加计算。

2.4 涡粘系数

涡粘系数根据Smagorinsky公式确定:

式中u、v分别为x、y方向垂线平均流速;Δ为网格间距;Cs为计算参数,0.25＜Cs＜1.0。

3 模型计算及分析

3.1 模型计算范围

数学模型计算范围上起长江上荆江公安河段观音寺,下至新厂,全长约51.1 km,见图 2。进口边界采用防洪设计流量56000 m3/s控制,出口边界为防洪设计水位38.91 m控制。整个区域剖分采用30 m×30 m的正方形单元网格,共有约44万个计算单元。计算地形为2008年6月实测1/10000地形图。

3.2 模型的验证

模型验证采用2008年11月22日的实测资料进行验证。图3为模型水位及流速验证图。由图3可见,计算值与实测值误差＜±0.03 m,说明计算水面线与实测水面线吻合较好,水位验证精度满足计算要求;流速误差一般＜±0.10 m/s,计算流速分布主流位置与实测值基本吻合,较好地反映了断面流速分布的变化趋势。

3.3 桥墩的概化

采用局部地形和局部阻力修正法:

局部地形修正根据桥墩设计尺寸对工程局部网格高程进行修正,使修正后的地形能反映桥墩对水流的影响,即阻水面积与实际桥墩阻水面积相当[5]。

桥墩的存在引起其局部阻力增加,因此要对模型中桥墩附近进行加糙处理。将桥墩作为断面突然收缩的阻水建筑物来考虑,其局部水头系数ξ采用下式计算:

式中A1、A2分别为工程前后断面过水面积。

再将局部水头损失系数转化为桥墩糙率的形式:

因此工程后桥墩所在网格节点的局部综合糙率为:

最后计算得桥墩所在网格综合糙率约为0.040～0.055。

图3 水位及流速对比图Fig.3 Water level and velocity comprision between computed and observed value

3.4 计算结果分析

3.4.1 水位变化分析

数学模型计算所得工程建成前后局部水位变化等值线图见图4。由图4可见,工程建成后仅在主桥墩附近一定区域内水位发生变化。水位壅高值＞0.02 m的影响范围至桥位上游1320 m,水位降低值＜-0.005 m的影响范围至桥位下游950 m。物理试验结果为桥位上游1000 m断面水位壅高0.028 m,桥位上游2000 m断面水位壅高0.015 m。因此,从工程建成后水位变化的幅值及影响范围方面来看,数学模型计算结果和物理模型试验结果基本一致。数学模型计算结果表明工程后主桥墩上游水位最大壅高0.066 m,主桥墩下游水位最大降低0.043 m。物理模型试验结果为主桥墩上游水位最大壅高0.076 m,主桥墩下游水位最大降低0.055 m。因此,从局部水位最大变化值方面来看,数学模型计算结果与物理模型试验结果比较接近。

图4 水位变化等值线图Fig.4 Contour map of water level change

3.4.2 流速变化分析

图5 流速变化等值线图Fig.5 Contour map of water velocity change

数学模型计算所得工程前后流速变化等值线见图5。由图5可见,工程建成后流速变化区沿河道纵向呈带状分布。在北侧主桥墩左侧流速增加＞0.05 m/s范围在桥位上游130 m至下游800 m以内;北侧主桥墩上下游流速减小0.05 m/s为桥墩上游150 m至下游1600 m以内;两个主桥墩之间流速增加＞0.05 m/s范围在桥位处至其下游3900 m以内;在南侧主桥墩上下游流速减小0.05 m/s的范围在桥墩上游150 m至下游4600 m以内;南侧主桥墩右侧流速增加＞0.05 m/s范围在桥位上游300 m至下游1280 m以内。物理模型试验结果表明断面流速＞0.05 m/s的影响范围为桥位上游1000 m至桥位下游3000 m。由此可见,在桥位上游流速变化影响范围数学模型计算结果比物理模型试验结果偏小,而桥位下游流速变化影响范围数学模型计算结果比物理模型试验结果则偏大。

3.4.3 流场变化分析

数学模型计算所得工程前后局部流场图分别见图6～图7,对比工程前后的流场图可以看出,建桥后主流线位置、平面流场分布没有发生明显变化。物理模型试验结果同样也表明工程建成后将不会对本河段的主流线位置、平面流场分布产生明显影响。

图6 工程建成前局部流场图Fig.6 Local velocity field before the project constructed

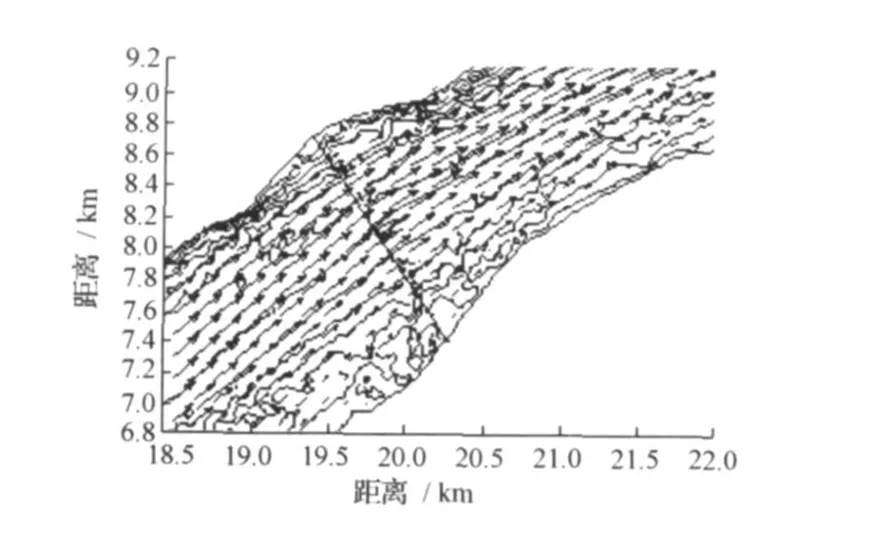
图7 工程建成后局部流场图Fig.7 Local velocity field after the project constructed

4 结 论

1)利用丹麦MIKE21软件建立长江上荆江公安河段平面二维水流数学模型,采用局部地形修正和局部糙率修正的方法概化桥墩对水流的影响。

2)通过在工程建成后桥位附近水位、流速、流场变化等方面,对比数学模型计算结果和物理模型试验结果,验证了该数学模型能够较准确地模拟工程对河道水流的影响,并得出工程建成后不会对工程河段的防洪及河势稳定带来明显不利影响的结论。

[1]胡春燕,王永忠,徐照明,等.长江口平面二维水沙盐数学模型研究及应用[C]//中国水力发电工程学会水文泥沙专业委员会第七届学术讨论会,2007.

[2]董耀华,林木松,魏国远,等.新建铁路荆州至岳阳线公安长江大桥定动床河工模型试验研究报告[R].武汉:长江科学院,2009.

[3]杨国录.河流数学模型[M].青岛:中国海洋出版社,1993.

[4]张永刚.桥梁壅水的计算[D].北京:北京交通大学,2006.