预测飞行路径透视显示方法研究

程建锋， 董新民， 薛建平

(空军工程大学工程学院，西安 710038)

0 引言

在飞行员操纵指令信号显示方法中，传统的显示器仅仅提供了相对于飞机当前状态的二维平面信息，驾驶员要通过这些信息重构飞机的时空情景，增加了负担［1］。而带有预测器的透视飞行路径显示不仅以隧道的形式提供给飞行员指令信息，而且还以三维的形式提供给飞行员预测位置信息，飞行员只需在一个接近真实情景中控制飞机沿隧道中心飞行，即可完成对航迹的控制，从而大大减轻了驾驶员的负担。

预测飞行路径显示有多种算法，文献［2］中给出了“圆形预测算法”和“全围预测算法”，文献［3］应用这些算法设计了横侧向预测显示器，文献［4］基于人工控制理论从驾驶员角度进行了分析，文献［5］对纵向和横侧向通道预测显示器进行了初步的设计。但是，目前对该问题的研究主要集中在横侧向通道方面，而将预测显示算法应用于纵向通道还不多见。文中将传统的基于圆形路径预测的显示方法应用于纵向通道的设计。首先，应用人工控制理论对其特性进行分析，指出其品质缺点;其次，采用基于q反馈的“非圆形预测”算法改进了传统的算法，最后通过理论分析和仿真验证其有效性。

1 带预测器的路径显示与补偿控制

带预测器的飞行路径显示方法提供给驾驶员飞机基于当前状态预测的位置信息和指令路径信息，如图1 所示［6］。

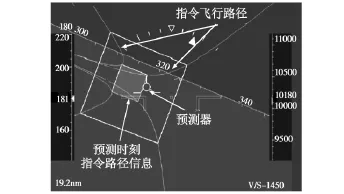
图1 带预测器的透视飞行路径显示图Fig.1 Perspective flight-path predictor display map

其中，预测器显示的是根据飞机当前的姿态、速度、加速度等参数预测的未来TPR时刻后飞机的位置，指令飞行路径是以“隧道”的形式显示的。预测器与对应预测时刻的“隧道”的交叉部分提供了预测位置偏差信息［7－8］。驾驶员利用这些偏差信息，采取“补偿控制”的方式操纵飞机使其沿隧道中心飞行。“补偿控制”是人工控制的一种重要方式，人工控制理论指出:为了兼顾系统的操纵特性和减轻驾驶员负担的双重要求，控制系统(驾驶员除外)在穿越频率附近应具有如下所述的特性［9］，YPR(s)YC(s)近似为一个积分环节，即:

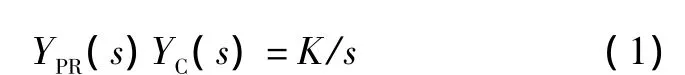
式中:YPR(s)为预测器传递函数;YC(s)为飞机模型。并且积分特性在穿越频率附近要有足够的带宽，同时还需要考虑以下因素:人机系统的稳定性、对扰动的灵敏性等。

2 基于圆形飞行路径预测的显示方法

预测器提供了飞机TPR时刻后的位置信息，文中采用“圆形预测法”，应用二阶泰勒展开式，TPR时刻后的飞机纵向的位置为［1］

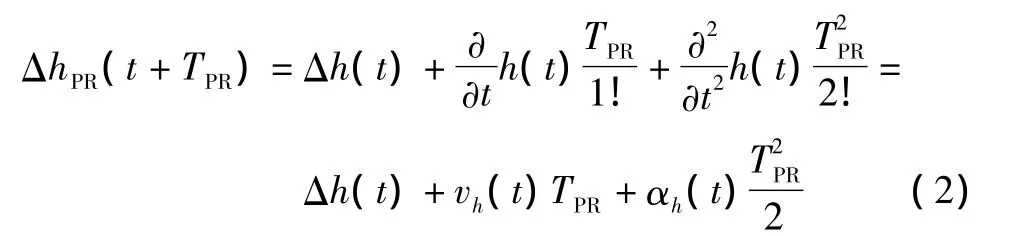
假设预测时间很短，飞机速度V为常数，航迹角满足式(3):

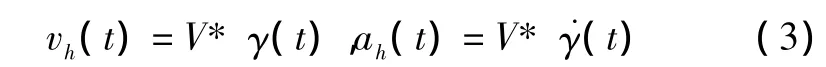
其中:TPR为预测时间。上式可表示为图2。

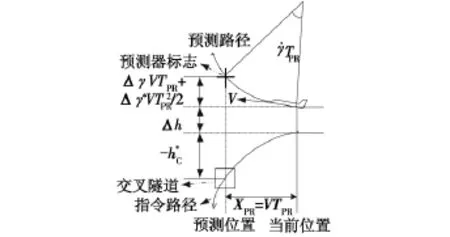
图2 “圆形预测法”原理图Fig.2 Principle of the circular flight-path predictor

根据控制理论，可以把未来时刻的偏离用当前时刻飞机的运动来表示，如图3所示。

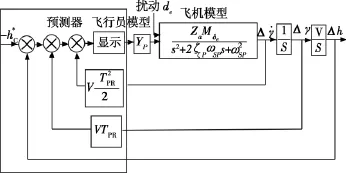
图3 圆形飞行路径预测显示原理方框图Fig.3 Block diagram of the circular flight-path predictor

结合图3，式(2)的Laplace变换为

式中:ePR为显示误差;KPR为显示增益。联合式(5)和式(6):

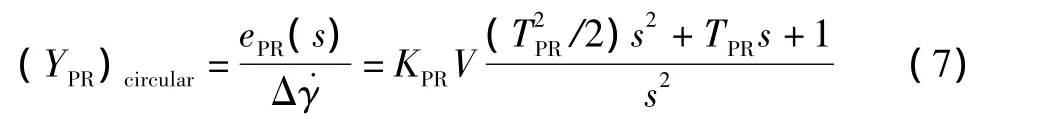
式(7)的分子多项式可化为

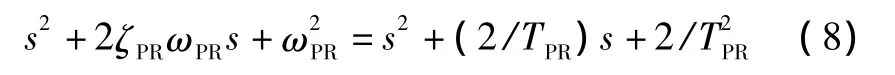
式中:ωPR=/TPR;ζPR=1/

假设飞机的模型为

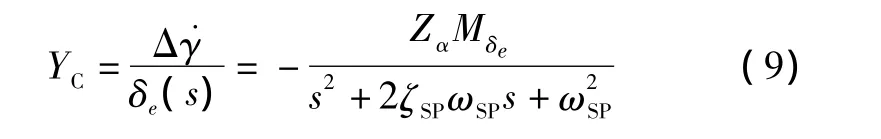
因此:

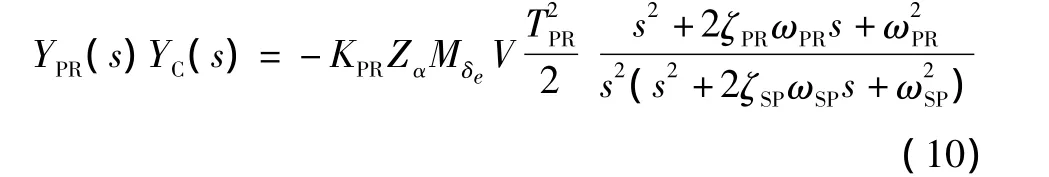
系统的Bode图如图4所示。

由图可见，系统在穿越频率处的响应近似为一个比例环节，不能够完全满足人工控制的相关要求。同时，由于反馈中引入了相对于˙γ的较大的反馈量/2，也导致了它对扰动的灵敏度大。

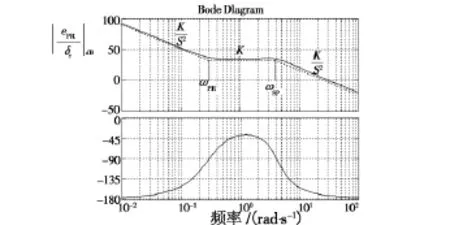
图4 圆形预测法预测器－飞机系统Bode图Fig.4 Bode plot for predictor-aircraft system with CPFP display method

3 基于q反馈的路径预测显示方法

为了克服以上缺点，用q反馈代替原来的˙γ反馈，如图5所示。

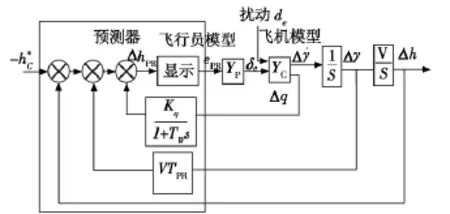
图5 基于q反馈飞行路径预测显示原理方框图Fig.5 Block diagram for predictor-aircraft system based on q-feedback theory

根据图5:

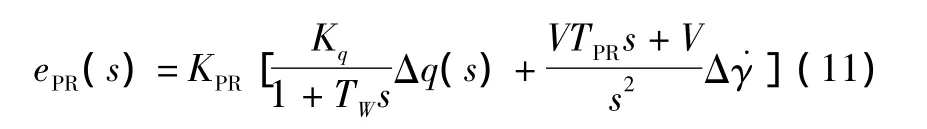
根据飞机间的变量关系为

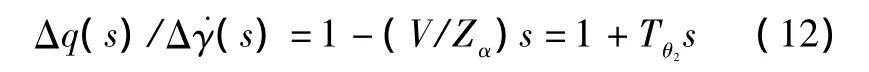
把式(13)代入式(12):

取 TW=Tθ2，式(14)可简写为

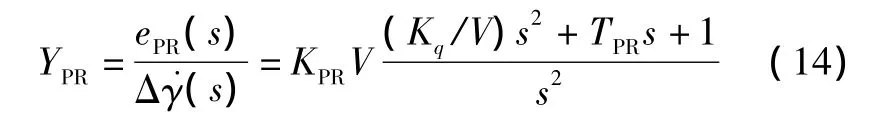
分析式(14)可以得出，通过调整Kq和TPR，可以使YPR(s)拥有两个实根，而非一对共轭复根，从而可以使系统满足人工控制理论相关要求。

为了满足上述要求:假设式(14)的分子为

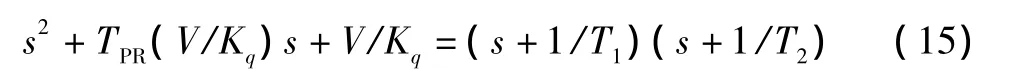
所以:

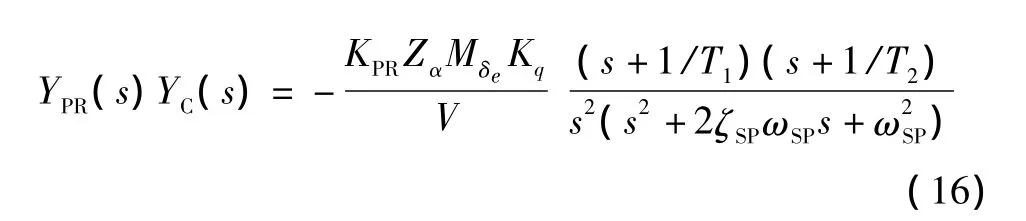
下面将依据式(16)对改进型系统的特性分析如下。

1)K/s要求。通过调整不同的T1，T2即可满足。

2)穿越频率出积分段带宽要求。为了保证积分段有足够的带宽，假设:T2＜＜T1，

所以:

根据上面分析，式(16)示意Bode图如图6所示。

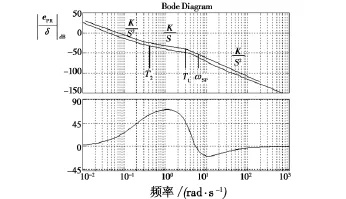
图6 q反馈法系统示意Bode图Fig.6 Bode plot for predictor-aircraft system based on q-feedback

通过分析可得:在T2和T1之间可以产生积分特性，并且可以使T1接近ωSP，从而保证系统有足够的带宽。而这些要求都是通过合理选择Kq和TPR来满足的。根据式(17)确定:

3)抗干扰性分析。q反馈飞行路径预测器比基本预测器的抗干扰性大大增强，因为，与前者相比，q反馈中最易受影响的变量的系数Kq大大减小了，从图3和式(18)可以看出:

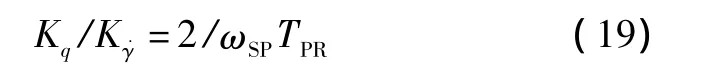
取 TPR=5 s，ωSP＞2 rad/s，则:

所以，采用q反馈大大降低了干扰对系统的影响。并且，当 ω ＞1/Tθ2时，q反馈型的1/1+TWs也会明显起作用，降低干扰的影响。

4 仿真分析

选取飞行状态V=240 m/s，H=10 000 m，飞机短周期方程为［10］

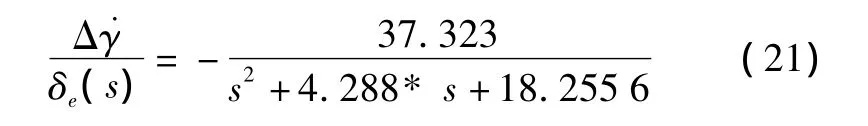
驾驶员模型取经典的McRuer模型［11］:

其中:Kp是驾驶员等效增益，取为1;τ为驾驶员反应延迟，取为0.2;TL和TI分别为超前和滞后补偿的时间常数，分别为 0.3 s和 0.5 s。

风的模型假设为一个随机扰动。

预测时间TPR=5 s，飞行路径显示器的任务是指引飞行员下降500 m，分别按照图3和图5进行仿真，结果见图7，图8。

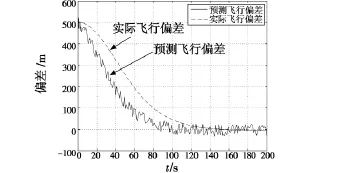
图7 圆形飞行路径预测显示仿真图Fig.7 Simulation results of CPFP display method

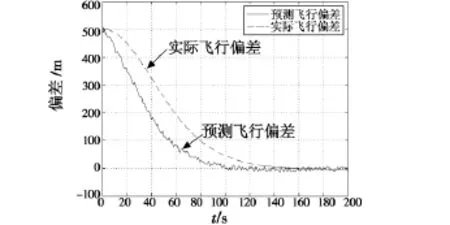
图8 q反馈飞行路径预测显示仿真图Fig.8 Simulation results of q-feedback-based display method

从图中可以看出，预测飞行偏差比实际飞行偏差超前一段时间，体现了预测器的作用;相比于传统的显示方法，改进型显示方法能够大大降低扰动对显示的影响。

5 结论

对比以上两种方法，基于圆型预测显示方法的物理意义明确，它是假设在预测的TPR时间段内飞机保持当前时刻的曲率飞行，而q反馈实质上是一个“非圆形预测法则”，它用较小曲率Kq代替了较大的曲率Kγ。但是，它又比较符合实际，因为在TPR时间段内(通常为5～7 s)，驾驶员会不断地操纵飞机来减小误差。从而减小了飞行轨迹曲率，可以看出，q反馈实质上在理论位置与实际位置之间进行了折中，同时，采用q反馈，物理上也比˙γ反馈容易实现。

通过以上分析，采用q反馈有效地克服了纵向圆形预测显示方法的缺陷，改善了人机闭环系统的性能。

［1］张德斌，郭定，马利东，等.战斗机座舱显示的发展需求［J］.电光与控制，2004，11(1):53-55.

［2］GRUNWALD A J.Predictor law for pictorial flight displays［J］.Journal of Guidance Control and Dynamics，1985，8(5):545-552.

［3］SACHS G.Improved predictor control law for tunnel display［R］.AIAA:2006-6220，2006.

［4］SENNES U.Perspective flight path and predictor display with two-axis control coordination［R］.AIAA:2000-4450，2000.

［5］SACHS G.Perspective predictor flight-path display with minimum pilot［J］.Journal of Guidance Control and Dynamics，2000，23(3):400-429.

［6］SWEET B T.Modeling of perception and control of attitude with perspective displays［R］.AIAA:2005-5891，2005.

［7］STURHAN I.Predictor-tunnel display with audio-visual aids for improving flight path control［R］.AIAA:2007-6420，2007.

［8］LAN T M，MULDER M，van PAASSEN M M.Comparison between augmentation techniques for tunnel-in-the-sky displays［R］.AIAA:2004-5238，2004.

［9］高金源，李陆豫，冯亚昌.飞机飞行品质［M］.北京:国防工业出版社，2003.

［10］鲁道夫.飞行控制［M］.肖业伦，译.北京:国防工业出版社，1999.

［11］袁修干，庄达民，张兴娟.人机工程计算机仿真［M］.北京:北京航空航天大学出版社，2004.