基于逆系统的赖氨酸发酵多变量解耦内模控制*

孙晓天 ，靳其兵，张 瑶，徐海涛

（1.北京化工大学 信息科学与技术学院 ，北京 100029；2.江苏大学 电气信息工程学院,江苏 镇江212013）

赖氨酸发酵过程是一个时变、非线性的多变量耦合系统，涉及到微生物细胞生长代谢的复杂过程,影响因素复杂,参数相关性严重[1-2]。如何实现具有非线性、多变量强耦合的生物发酵过程的解耦控制已引起生物界的关注。解耦控制的实质是针对一个具有耦合的多输入、多输出的控制系统,通过串联一个前馈补偿器，把耦合限制在一定程度或者解耦成多个独立的单输入单输出系统[3]。

传统的逆系统方法的一个比较重要的缺点是被控非线性系统的数学模型必须精确可知[4-5]，而这在发酵工业中很难满足，即使能够建立非线性数学模型，利用复杂的非线性模型也极难求得逆模型的解析解。参考文献[6]是用支持向量机外加若干积分器一起构成支持向量机逆系统，但积分器的误差比较大。为了减少误差并使网络具有动态特性，本文选择动态递归模糊神经网络[7-8]对逆系统进行辨识。

动态递归模糊神经网络，作为模糊逻辑和神经网络的有机结合体，兼备模糊逻辑和神经网络的优势，不仅能处理模糊信息，实施模糊推理，而且引入神经网络的学习机制，增强了网络的自适应能力，使得模糊神经网络同时具有推理能力强和自适应能力强的优点,具有很强的辨识能力；动态递归模糊神经网络还可以用网络内部节点间的反馈去描述系统内部的动态关系；它在运行过程中，利用了当前数据和历史数据，充分反应了系统的动态过程，因此它比较适合于动态非线性系统的辨识建模。

本文用动态递归模糊神经网络来构造原系统的“逆系统”,将对象补偿成为具有线性传递关系的且已解耦的一种规范化系统,再分别对各解耦子系统设计内模控制器,从而实现对原非线性耦合系统的高性能控制。

1 赖氨酸发酵过程逆模型

以下是赖氨酸发酵过程动力学模型:

4个状态变量 x1～x4分别是：菌体浓度 X(x1)、基质浓度 S(x2)、产物浓度 P(x3)、发酵液体积 V(x4)，3个输入量u1～u3分别是各种补料流加时蠕动泵流加速率,即碳源(葡萄糖)流加速率 fc(u1)、氮源((NH4)2SO4)流加速率 fn(u2)、氨水流加速率fph(u3)。其中ki(i=1,2,3)都是非零常数，而μ、σ、π均为状态变量的解析函数。

以3个流加速率u1～u3作为输入控制量，4个状态变量中的前 3 个 X(x1)、S(x2)、P(x3)作为 被控量 ，V(x4)作为状态量，建立如下的发酵过程的系统数学模型：

[6]知(1)式的逆模型为：

然后用DRFNN网络辨识(2)式，将辨识好DRFNN网络与发酵系统复合成为近似的伪线性系统,如图1所示，该系统基本上实现了输入输出线性化。

2 动态递归模糊神经网络

构建多输入多输出动态递归模糊神经网络结构共分为5层，如图2所示。在下面的表达式中，xi表示输入表示第 k层的第 i个输入表示第 k层的第 i个输出表示递归连接权值是归一化层到输出层的连接权值，图中未标出的各层节点之间的权值都为1。网络各层之间的输入输出关系如下：

第1层为输入层，该层的节点直接与输入量x=[x1,…,xn]T连接，作用是将x传送到下一层。

第2层为模糊化层，该层每个节点代表一个隶属函数，且神经元的激励函数是高斯函数。其中输入输出分别为：

cij、σij为隶属函数的中心和宽度。 i=1,…,n，j=1,2,…，mi,mi是xi的模糊分割数。

第3层为规则层，该层的节点代表模糊逻辑规则的前件部分，是用来匹配模糊规则的前件。其中输入输出分别为：

第5层为输出层，其中输入输出分别为：

3 网络参数学习算法

式中yd(k)、y(k)分别是k时刻系统实际的输出和动态递归模糊神经网络的输出，n为学习样本数。采用误差反串算法对网络的主要参数进行调整。

(1)隐层到输出层的权值调整公式:

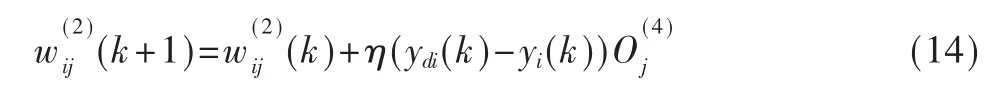
(2)递归层到隐层的权值调整公式:

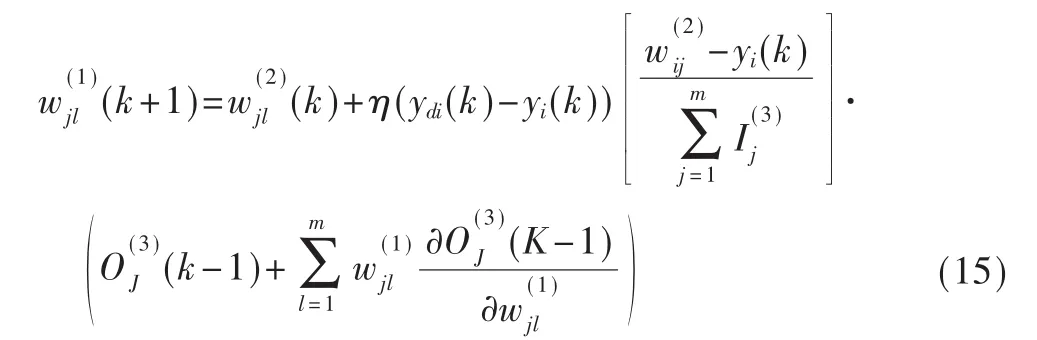
(3) 参数 cij、σij的 调整公式

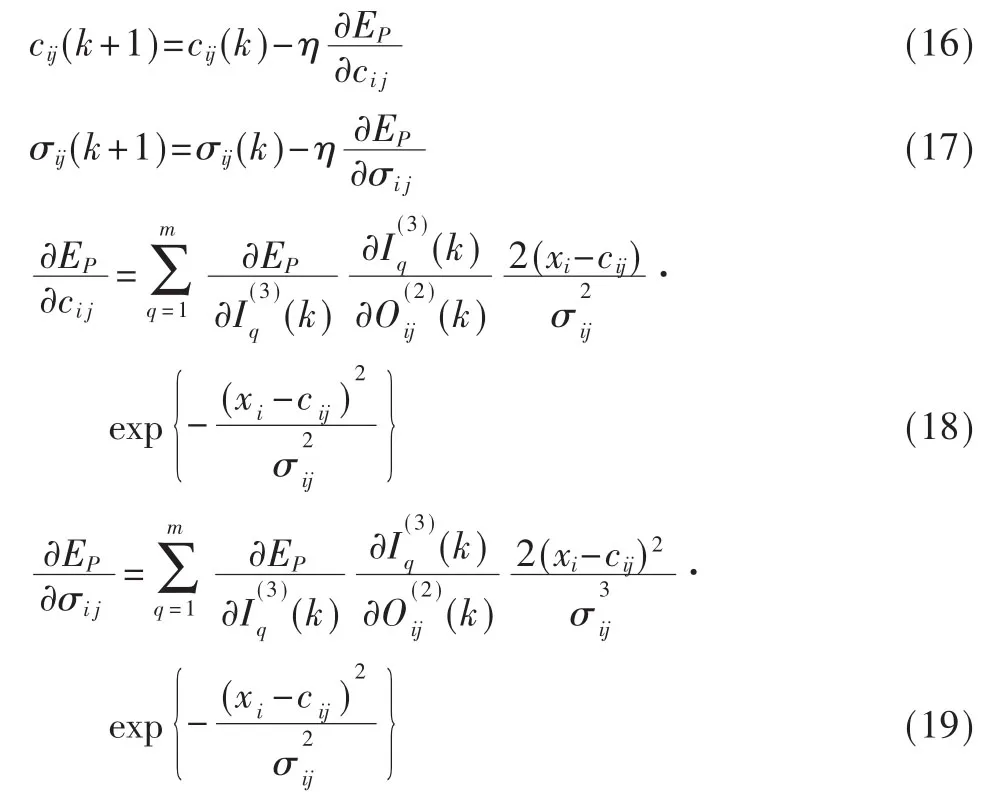
式中η是神经元学习率。

将动态递归模糊神经网络的递归层去掉，则动态递归模糊神经网络就成为传统的静态模糊神经网络，因此递归层的初始权值可设为0，网络的其余主要参数可用下述方法确定。

由上述数据(x(i)，ud(i))i=1,2,…,p,可求 得:

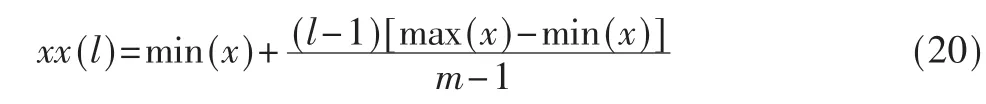
分别求 p个 x中与 xx(l)靠得最近的 m个x(l)，使

x(l)与 yd(l)是对应的并且有：

式中 j=1,2，…，m，l=1,2,…,m

4 基于逆系统的赖氨酸发酵解耦内模控制

由于逆系统方法获得的伪线性系统不存在反馈，所以对图1的伪线性系统采用内模控制。非线性内模控制系统的结构如图3所示，在图3中，G(s)为过程模型的传递函数，GIMC(s)为内模控制器的传递函数，F(s)为滤波器。

当存在模型失配时，为确保模型的稳定性，引入滤波器。通过对它的适当设计，可以改善IMC系统的鲁棒性，且其鲁棒性的强弱可以方便直观地调节参数；同时可以起到柔化控制，平滑输出的作用。

由系统的相对阶α=(1,1,1)T可取内部模型:

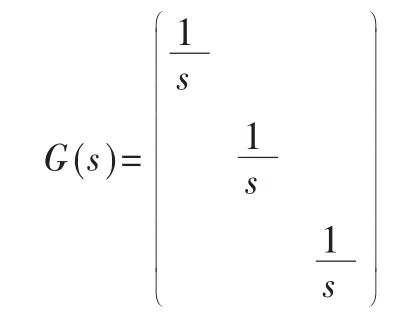
则加上滤波器后的内模控制器C(s)=F(s)GIMC(s)=F(s)G-1(s)。F(s)为一型滤波器，且1,2,…,n。

5 仿真结果与分析

5.1 DRFNN网络的训练

式(1)中的第4个方程为发酵液体积V与3个输入量之间的关系，显然只要输入量一定，隐动态－发酵液体积是稳定的，因此训练样本集为{{x1,x2,x3},(u1,u2,u3}}。从建成的生物发酵数据库中提取8批数据，对全部的数据进行数字滤波(滑动平均滤波法)处理。前7批数据作为训练样本，最后1批作为测试集。

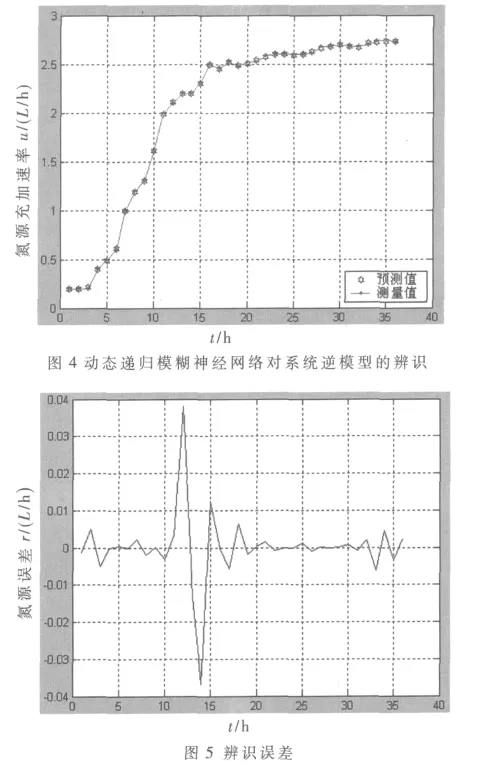
取DRFNN网络的初值x1=0.34，x2=148，x3=0.12。在DRFNN训练过程中,设学习率为0.1,目标误差为0.01,训练次数为 2 000。最后DRFNN网络结构为(3-6-36-36-3)，其中 mi=2。在辨识过程中，图4是 DRFNN对逆模型的输出-氮源流加速率的辨识结果，图5是其辨识误差。

5.2 控制分析

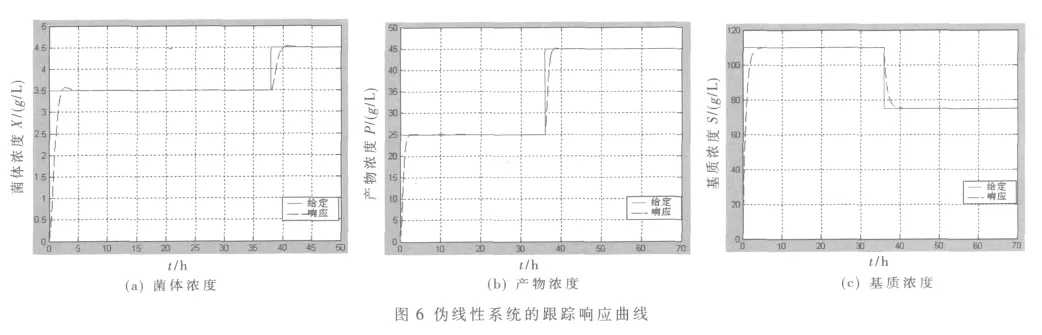
采用图3的控制结构，选用输入信号为方波信号，这时原系统为三输入三输出系统，其中滤波器的参数分别为 λ1=0.7，λ2=0.5，λ3=0.8。 由图6 可以看出，内模控制对发酵系统具有理想的控制效果。

本文利用DRFNN网络对赖氨酸发酵过程的逆模型进行辨识，同时将逆系统方法与内模控制器相结合，提出了基于逆系统的赖氨酸发酵多变量解耦内模控制方法。仿真结果表明，该方法能较好地实现输出变量的解耦控制，从而为MIMO非线性解耦控制提供了一条新的途径。

参考文献

[1]孙玉坤,陈明忠,嵇小辅,等.基于支持向量机的赖氨酸发酵生物参数软测量[J].仪器仪表学报,2008,28(10):2066-2071.

[2]MONTAQUE G A,MORRIS A J.BUSH J R.Consideration in control scheme development for fermentation process control[J].Control Process System IEEE,2002,8(2):44-48.

[3]WANG Qing Guo,ZHANG Yu,CHIU Min Sen.Decoupling internal model control for multivariable systems with multiple time delays[J].Chemical Engineering Science,2002,57:115-124.

[4]WINDOW B,WALACH E.Adaptive inverse control[M].NewJersey:Prentice Hall,1996.

[5]卢志刚,吴士昌.非线性自适应逆控制及其应用[M].北京:国防工业出版社,2004.

[6]黄永红 ,孙玉坤,王博,等.基于最小二乘支持向量机逆系统的赖氨酸发酵过程解耦控制[J].信息与控制,2009，38(3):365-369.

[7]张友旺,桂卫华，赵泉明.基于动态递归模糊神经网络的自适应电液位置跟踪系统[J].控制理论与应用,2005,22(4):551-556.

[8]TOMMY W S,YONG Fang.A recurrent neural network based real time learning control strategy applying to nonlinear system with unknown dynamics[J].IEEE Trans Industrial Electronics,1998,45(1):151-161.