钛酸钡中极化团簇的特征弛豫时间随温度的变化规律
宋春立 严 睿 郭 智 邰仁忠
(中国科学院上海应用物理研究所 上海 201800)
某些电介质材料在一定温度范围内具有自发极化特性,在自然状态下,自发极化方向随机分布;在外加电场作用下,自发极化方向会随外电场变化。这种特性称为铁电性,具有铁电性的材料称为铁电体。铁电体具有独特的声、光、电、力和热学等性质,且具有性能耦合或转换功能,在超声设备、通讯设备、人工智能、存储器等方面有广泛应用[1]。
BaTiO3是优异性能的铁电体材料。起初人们用位移型相变[2]来解释BaTiO3的种种特性,但很快发现问题并不简单。X射线散射实验[3]和准弹性中子散射实验[4]证明,BaTiO3有两种相变机制:有序机制和无序机制。这两种相变机制可以共存,Zalar B等[5]根据NMR实验提出了两种相变共存的可能性。Stachiotti M等[6]用分子动力学模拟理论研究对铁电体相变,表明BaTiO3中存在极化团簇。Bakker H J等[7]提出 BaTiO3相变点处的介电响应源自极化团簇的弛豫行为和晶格软模波动的强烈耦合,即极化团簇的空间、时间信息以及随温度的演化信息在介电性质形成过程中发挥着重要作用。因此,探测BaTiO3中极化团簇的相关信息对于理解其功能、揭示相变机理具有重要意义。2004年,邰仁忠等[8]用X射线激光散斑技术,首次观测到BaTiO3中极化团簇的空间结构。
用光子相关谱技术(Photon Correlation Spectroscopy,PCS)研究粒子系统的尺寸分布、扩散进程、运动弛豫等,具有所需样品量少、对样品无损等优点。Yan R等[9]用 PCS法得到 BaTiO3中200nm 周期的极化区域的特征弛豫时间(τc)随温度的变化关系,并发现特征弛豫时间在居里点(TC)附近存在突变,但因实验条件的限制并未得到该突变的细节信息。我们对PCS法测试装置作了改进,用透镜聚焦减少漫反射,用高精度稳频温控装置控制样品架温度,获得了居里点TC附近4 K范围内的大量统计数据,揭示了特征弛豫时间在此温度范围内突变的细节特征。
1 样品与装置
BaTiO3晶体为熔融法生长,居里温度TC=399 K,沿晶向切割成5 mm×5 mm×1 mm晶片,选择晶体的(001)面(c轴方向)作为散射光的入射、出射面。为提高样品的光学性质,对样品的入出射面做了抛光处理。我们对本实验的如文献[10]中光路图做了两点改进(图1):把温控仪为日本岛通MAP6A系列,温控精度±0.02 K;在激光器和Polarizer I间插入一个聚焦镜,让激光器的能量更集中,得到更强的散射光。此两项改进使我们获得更稳更强的实验信号。
图1实验光路中,激光经垂直偏振片I(Polarizer I)后得到线偏振光,垂直照射到样品上。以往实验的散射角大,导致的采光困难和强度不稳定,本实验选取由Slit取出固定点P处散射角θ=52°的散射光进行采集和运算。水平偏振片II(Polarizer II)与垂直偏振片I正交,仅允许经极化团簇调制后改变了偏振态的光通过,因此散射光中仅含有极化团簇的信息。干涉滤光片用于消除大部分的非弹性散射,筛选中心波长。为提高散射矢量单色性,Polarizer II后放置针孔光阑,并用透镜聚焦,以收集更多的散射光。透镜后的5/5分光镜将散射光等强度分成两束,通过光电倍增管(PMT)输出到相关仪,进行g(τ)=

图1 光子相关谱实验装置俯视图Fig.1 A top view of the PCS experimental setup.
2 实验原理
实验采用双偏振片滤波抑制背底和强度相关的方法,提取并处理隐藏在噪音中微弱的、由极化团簇弛豫行为引起的强度随时间涨落的散射信号,对BaTiO3单晶中极化团簇的弛豫行为实施直接观测。极化团簇对散射光场的调制,可用Fraunhofer单缝衍射模型作简化说明(图2)。
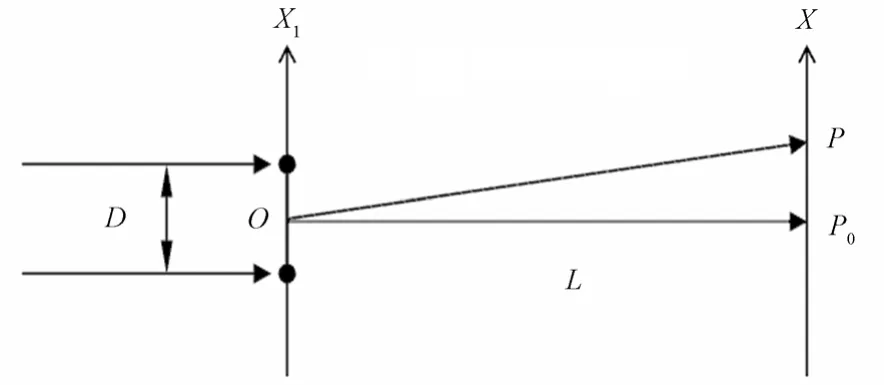
图2 夫琅和费衍射模型Fig.2 Fraunhofer diffraction model.
设极化团簇的平均周期尺寸为D(即相邻两团簇的间距),选取两个团簇中心作为坐标原点O,由Fraunhofer衍射公式,在距样品L处的P点有:
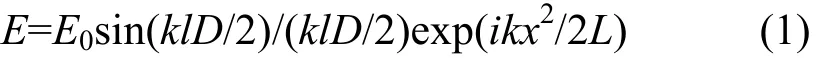
其中,E为该点的振幅,E0为原点O的振幅,k为入射光的波数,x为P与P0之间的距离,L为O到P0的距离,l为x/L。在热激发条件下,极化团簇是动态的,可根据Debye弛豫模型描述极化团簇的间距离随时间的变化:

其中,D0为初始距离,函数峰值1/e处的时间τc即定义为极化团簇的特征弛豫时间。实验测得的是在固定散射角P点狭缝后的强度波动,由于分束镜等强度分光,强度相关函数可进一步表述为:

其中τ为延迟时间,<>为强度的时间平均。将光场和振幅的关系I=EE*、Debye方程和P点振幅E,代入式(3),可得

由此,通过相关函数曲线的解析可以得到动态散射体(极化团簇)的特征弛豫时间。
以上推算仅是简化模型对单独个体的分析,而晶体中极化团簇的弛豫过程极为复杂,散射体积内团簇的不同弛豫形态随机分布,热激励所导致的极化团簇之间的藕合等因素,决定了相关谱实验观测的是此类强关联体系的集团平均效应。Alvarez等[10]对此类复杂体系的集团行给出数学表述为(称为KWW方程):
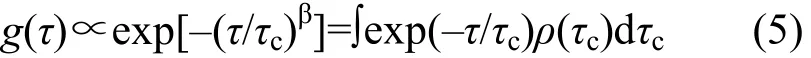
式中,exp(–τ/τc)为 Debye 弛豫函数,ρ(τc)为弛豫时间的分布函数,β为拟合修正指数。此方程广泛应用于复杂体系的弛豫过程的拟合,如动态光散射(即光子相关谱)、极化波动、介电弛豫等。本实验采用KWW方程进行不同温度下的相关函数拟合,提取1/e峰值处的特征弛豫时间,探寻其相变点的演化规律。对于P点,散射矢量[11]q=ki−kf,模值q=|q|=2nksin(θ/2)。所选温度范围为TC±2 K (TC为399 K),BaTiO3样品的折射率为2.4,计算得到散射矢量的模为 21 µm−1,对应的平均周期尺寸为D=2π/q≈300 nm,即实验所测为平均周期300nm的长程极化的特征弛豫时间。
3 实验结果和分析
本实验所用相关仪可采集τ从10−9s到103s之间的295个数据点。此前研究表明[9],在这种实验条件下,可观测的团簇的弛豫行为在微秒量级,故我们选取1 µs –20 ms间的115个值进行数据拟合。Matlab 软件中的拟合方程为g(τ) =Aexp(−bτ) +B,该方程对应于KWW方程β=1和b=1/τc时的情况。我们采用最小二乘法,令B等于最后20个函数值的平均值,并适当改变拟合起点的数值使τc置信区间达到最窄,拟合结果见图 3。图中圆圈表示相关仪采集的原始数据,实线为拟合曲线,箭头和方框标注了不同温度下τc的位置。
表1为从相关曲线中提取的不同温度下的特征弛豫时间τc及其置信区间,置信度为95%。由表1,温度从 397 K 到 399 K,τc从 4.00 µs增至 7.14 µs,而当温度再升到401 K,τc降为2.66 µs。由此可见,在温度TC±2 K范围内,τc具有随温度升高先增后减的变化规律;τc的最大值是最小值的两倍多。各相邻特征弛豫时间的置信区间无交叉现象,该置信度说明了该变化规律的统计可靠性。

图3 不同温度下的相关函数曲线,各个温度点的单次测量时间为9600 sFig.3 Intensity correlation function curves of the BaTiO3 crystal at different temperatures. In 9600 s measurement for each temperature.
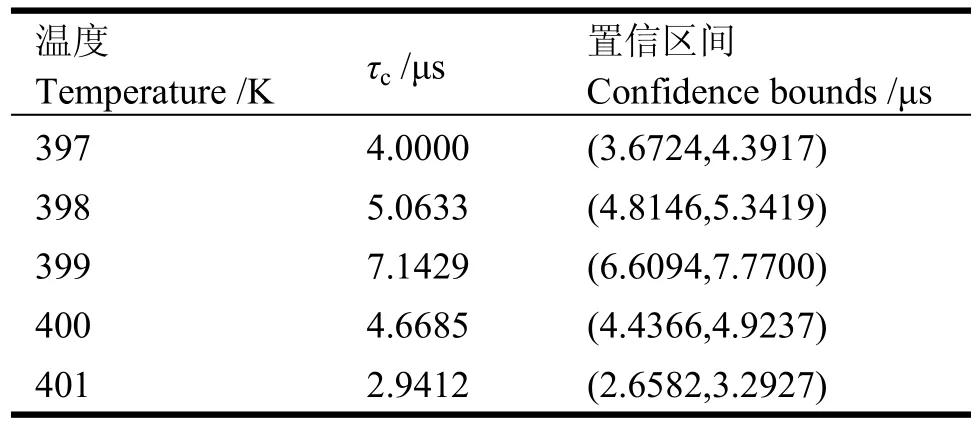
表1 不同温度下的特征弛豫时间及95%置信度的置信区间Table 1 Characteristic relaxation times(τc) and their 95%confidence bounds at different temperatures
研究表明,纳米量级的偶极子的弛豫行为是热激励作用的结果,其弛豫时间在ps量级,Namikawa等[12]采用软 X射线散斑强度关联方法观测到在TC温度附近,BaTiO3中偶极子的弛豫时间为20–90 ps,而由大量偶极子组成的长程极化团簇则拥有更长的弛豫时间。实验则发现在BaTiO3中周期约为300 nm的长程极化团簇的特征弛豫时间为µs量级,并且在居里点TC附近4 K的温度范围内,该时间具有先增后减的细节特征。Arrhenius law[13]将铁电弛豫行描述为τ=τ0exp(Ea/kBT),其中,τ0为高温下特征弛豫时间,Ea为激活能。由光子相关谱的实验结果可知,特征弛豫时间显然不是单调函数,所以Ea在居里点附近也不应常数,而是温度的函数。
另外,实验需尽量避免外界光的干扰,以提高信噪比。因此该实验在暗箱中完成的,信噪测试结果见表 2。样品架未放样品时,所测空气平均散射光强为0.075 kHz,称为本底暗噪;样品架上放置钠钙玻璃时,由于钠钙玻璃不含改变入射光偏振态的时间调制结构,在正交消偏振模式下散射光极少能进入探测器,因此测得各温度下平均散射光强为0.1kHz,选此噪音作为系统噪音;样品架上放置BaTiO3晶体时,晶体中极化团簇改变了入射光的偏振态,在正交消偏振模式下,平均散射光强可达到600 kHz,因此实验具有极高的信噪比。

表2 不同温度下的系统参数Table 2 System parameters at different temperatures.
4 总结
实验采用了高精度温控装置,从而在包含BaTiO3居里点的狭小温度范围内实施了光子相关谱的多次实验, PCS最终测量了BaTiO3中300 nm周期的长程极化团簇的时间信息,有效揭示了特征弛豫时间在居里点TC附近4 K温度范围内演化的细节特征:BaTiO3中极化团簇的特征弛豫时间在TC温度附近随着温度升高逐渐增大,在居里点TC处达到最大值,之后逐渐减小,形成先单增,后单减的变化特征。
1 Wadhawan V K, Prandit P, Gupta S M. Mater Sci Eng B,2005, 120: 199–205
2 Last J T. Phys Rev, 1957, 105(6): 1740–1750
3 Comes R, Lambert M, Guinier A. Solid State Commun,1968, 6(10): 715–719
4 Yamada Y, Shirane G, Linz A. Phys Rev, 1969, 177(2):848–857
5 Zalar B, Laguta V V, Blinc R. Phys Rev Lett, 2003, 90(3):037601-1–037601-4
6 Stachiotti M, Dobry A, Migoni R,et al. Phys Rev B, 1993,47(5): 2473–2479
7 Bakker H J. Phys Rev B, 1995, 52(6): 4093–4103
8 TAI Renzhong, Namikawa K, Savada A,et al. Phys Rev Lett, 2004, 93(8): 087601-1–087601-4
9 YAN Rui, GUO Zhi, TAI Renzhong,et al.Appl Phys Lett,2008, 93: 192908-1–192908-3
10 Alvarez F, Alegria A, Colmenero J. Phys Rev B, 1991,44(14): 7306–7312
11 Burns G, Dacol F H. Solid State Commun, 1982, 42(1):9–12
12 Namikawa K, Kishimoto M, Nasu K,et al. Phys Rev Lett,2009, 103(19): 197401-1–197401-4
13 Bidault O, Goux P, Kchikech M,et al.Phys Rev B, 1994,49(12): 7868–7873

