求解互联电网经济调度的层级协调方法

谢国辉 张粒子 舒 隽 杨 湛

（华北电力大学电气与电子工程学院 北京 102206）

1 引言

我国地区间的能源分布与需求不平衡，电源结构和负荷特性存在较大的互补性，地区间资源优化配置空间明显存在。开展互联电网经济调度对于提高电力系统运行经济性，促进资源优化配置具有积极现实意义。

求解互联电网经济调度的方法可分为集中和分解协调两种。集中方法能够一次性获得优化结果，显著提高计算效率，但是如果电网规模过大，其建模容量和优化算法的执行效率将受影响，因而目前更多关注分解协调方法。文献[1]基于直流潮流模型，通过多区域之间交换边界信息进行迭代求解，进而收敛到全局最优解；文献[2]在文献[1]的基础上，基于部分对偶理论分析了电网分区的分解协调模型，提出了一种基于直流最优潮流模型的互联电网多区域分解最优潮流的并行求解算法；文献[3-4]提出引入虚拟母线或虚拟发电机，并将其复制到各个区域的分解方法，并基于辅助问题原理的拉格朗日松弛算法，进行多区域最优潮流的分布并行计算；文献[5-7]提出不改变网络结构，仅在各区域中考虑联络线潮流影响的分解方法，文献[5]采用文献[6]提出的增广拉格朗日松弛的区域分解最优潮流算法求解多区域电力市场输电阻塞管理问题，而文献[7]采用全局优化变量方法求解交流最优潮流问题；在文献[3-4]基础上，文献[8-9]同样基于辅助问题原理方法，用于求解多分区并行无功优化问题。

本文针对我国目前多级调度管理体制现状，提出一种基于层级调度新的分解协调方法。建立区域协调中心和分区调度的层级协调运作机制，即各分区在区域协调中心给定的边界条件下完成本分区内的经济调度，而区域协调中心则根据分区反馈信息更新边界条件重新传递至各分区进行迭代优化。基于二次罚函数方法，构建区域协调中心和分区调度的层级协调优化模型，分别采用拟牛顿算法和原对偶内点算法求解。最后，通过 IEEE30算例验证本文所提出的层级协调方法的有效性。

2 层级协调运作机制

本文提出求解互联电网经济调度的层级协调运作机制，如图1所示。

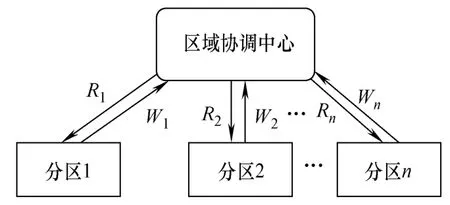
图1 层级协调运作机制Fig.1 Mechanism of hierarchy coordination

图1中，R1、R2和Rn分别是区域协调中心传递给分区1、2和n的边界变量（例如，分区间联络线母线节点的相角、电压幅值等）；W1、W2和Wn是分区1、2和n在给定边界变量下优化本分区经济调度后反馈回区域协调中心的信息集合。

层级协调具体运作机制是，区域协调中心初始化各分区边界变量传递至各分区，分区据此完成本分区域经济调度后反馈相关信息至区域协调中心，协调中心更新边界变量重新传递给分区进行迭代优化，如此反复，最终完成整个互联电网经济调度。

这种协调运作机制的优点在于：①各分区共享同一个区域协调中心，信息只在区域协调中心和各分区间传递，分区之间完全独立运作且无需彼此交换信息，从而简化了通信设置。②区域协调中心能够灵活调控各分区之间的边界变量，进而实现一对多的全局控制。③无需改变现有网络结构，方便开展分布式并行计算。④这种层级协调机制与目前我国多级调度管理体制相适应，既可以与现行调度模式衔接，又能够进一步优化配置资源。

3 层级协调优化模型

3.1 互联电网经济调度模型

多分区互联电网经济调度一般模型如下：

式中 n——互联电网分区数目，n=1，2，…，N；

θij——节点i和j的相角差；

PLi——节点i的有功负荷；

QLi——节点i的无功负荷；

f(PGi)——发电机组的发电费用函数；

Ui,,——节点i电压幅值和电压上下限约束；

Gij+jBij——节点导纳阵中的相应元素。

上述模型是互联电网经济调度的一般模型，约束条件不仅包括各分区自身约束，还包括分区联络线之间的耦合约束。实现各分区独立运作以及区域协调中心集中协调优化，其关键点和难点是如何对模型（1）中各分区间的耦合约束进行解耦。为此，采用协调边界变量方法对模型（1）进行重构，基于二次罚函数法将边界变量约束松弛进入各分区目标函数中，构建分区和区域协调中心各自优化模型，再采用有效算法进行求解，从而实现各分区间的解耦和层级协调运作。

3.2 互联电网经济调度模型重构

设有互联电网两个分区A和B，中间通过联络线ij连接。互联电网解耦过程示意图如图2所示。

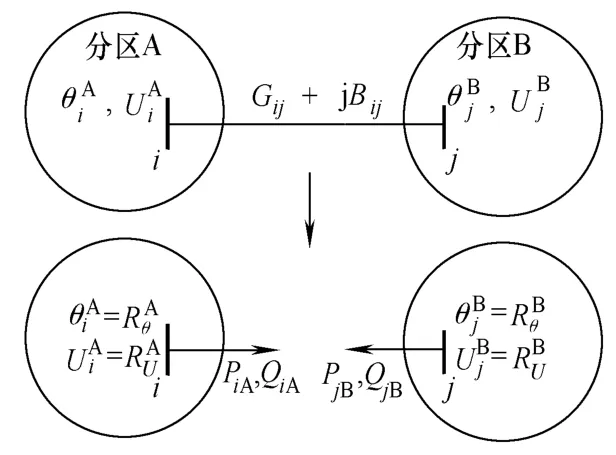
图2 互联电网解耦过程Fig.2 The proposed decoupling of interconnected power systems

图2中，R为传递给分区A和B的边界变量（分区间联络线母线节点的相角和电压幅值）。当给定的 R为分区 A和 B联络线 ij两端的相角和电压幅值后，分区间联络线的有功和无功可通过边界变量R计算得到，例如分区A联络线出口功率为

同理可以计算分区 B联络线的有功和无功功率。由于联络线功率可以通过R计算得到，那么分区A和B则可以在此边界条件下完成各自分区内的经济调度，实现了对互联电网经济调度的解耦，从而模型（1）可以重构为

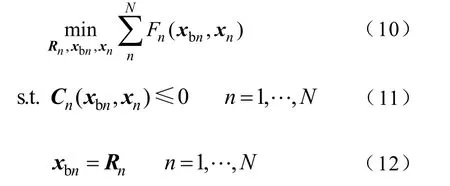
式中 Rn——传递给分区n的边界变量；

xbn, xn——分区n的边界变量和内部变量;

Fn(xbn,xn)——分区n目标函数;

Cn(xbn,xn)——分区n等式和不等式约束集。

3.3 基于二次罚函数法的层级协调模型

模型（10）是非线性约束优化问题（Constrained Optimization Problem，COP），本文采用序列无约束化方法（Sequential Unconstrained Minimization Techniques, SUMT）求解。序列无约束化方法[10]基本思想是用一个无约束优化问题的序列逼近约束优化问题，通过无约束优化问题的最优解序列，逼近约束优化问题的最优解。COP一般形式[10]为

式中 f (x)——目标函数；gi(x)，hj(x)——约束函数；ζ，σ——不等式约束和等式约束的指标集。

SUMT的核心内容是构造一个含有参数µ 的函数P ( x,µ)=(f (x),g( x), h( x))，使得∀x∉S（可行域），P（x,µ）≫f(x)；然后，通过极小化 P(x,µ)，获得一个与参数µ有关的极小点序列，逐渐逼近问题（COP）的极小点。函数P(x,µ)通常称为罚函数，参数µ 称为罚因子。从计算角度看，二次罚函数法的极小化过程能够比较方便地完成，其具体形式为

可以证明，当目标函数 f(x)，约束函数 g(x)和h(x)连续可微，序列{µk}严格递减趋向于零，迭代点列{xk}的任意一个极限点都是COP的全局最小点[10]。因此，本文采用二次罚函数方法对模型（10）进一步解耦，将其约束条件（12）以罚函数形式松弛到目标函数中。

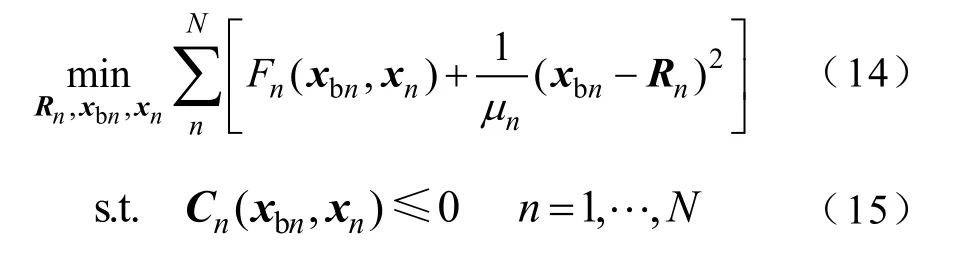
如此，模型（14）的约束条件已不再含有分区间的耦合约束，因而可以建立各分区和区域协调中心的层级协调优化模型：

（1）分区优化模型

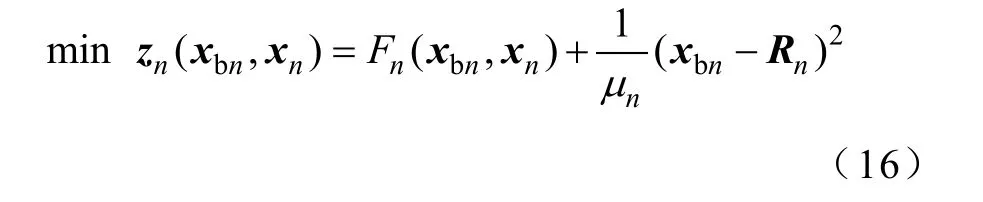
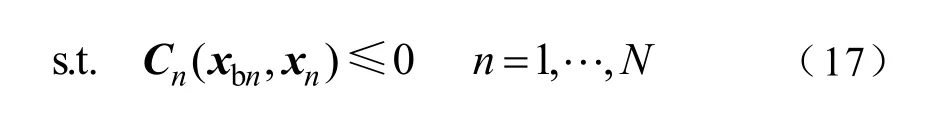
分区优化变量为本分区内各母线节点的相角、电压幅值以及发电机的有功和无功出力。

（2）区域协调中心模型

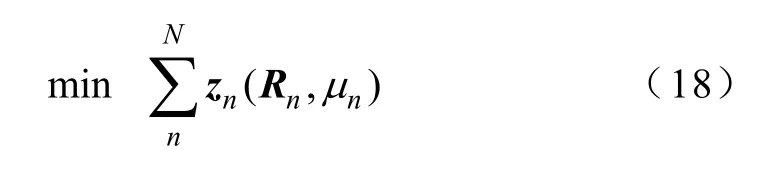
区域协调中心的优化变量为传递至各分区的边界变量Rn，其梯度为= -2 ()/为二次罚函数的罚因子。可以看出，通过二次罚函数方法解耦，模型（18）已转变为无约束的优化问题。

4 协调优化算法

4.1 区域协调中心算法

上述建立的区域协调中心优化模型（18）是非线性无约束优化问题，故本文采用非线性无约束优化问题的拟牛顿算法（quasi-Newton method）求解。拟牛顿法是一类收敛速度比较快的算法，现在，已经成为公认的比较有效的无约束优化方法。其近似矩阵的估计方法很多，其中BFGS公式是较为有效的方法。

本文求解区域协调中心模型（18）基于拟牛顿算法的BFGS[10]，具体迭代公式为

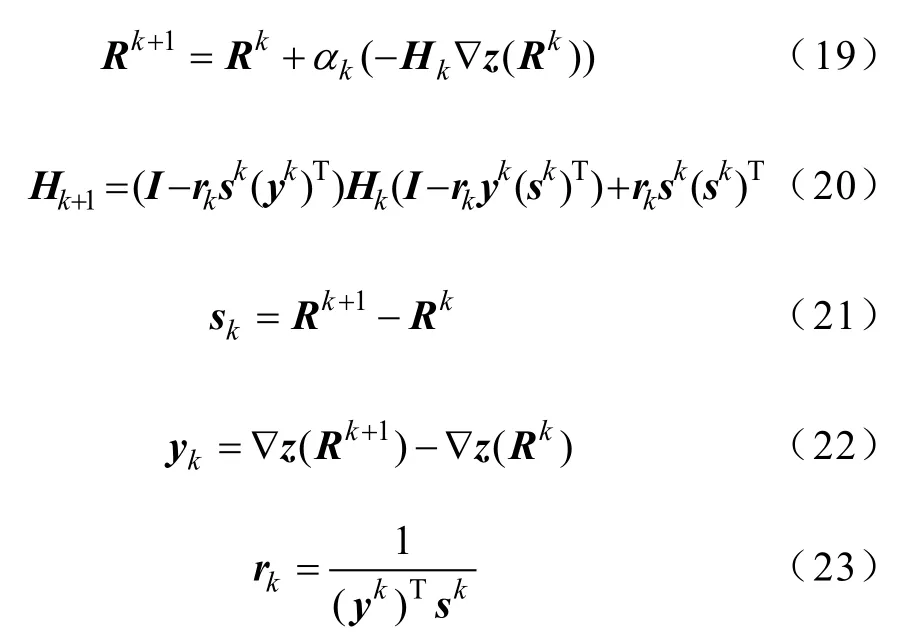
式中 Rk，Hk，αk——第 k次迭代的边界变量，近

似Hessian矩阵，搜索步长；I——单位矩阵；

区域协调中心停止信息交互的判断准则是各分区传递至区域协调中心的边界变量的梯度 2范数小于某个极小值ε。具体求解流程如图 3所示。

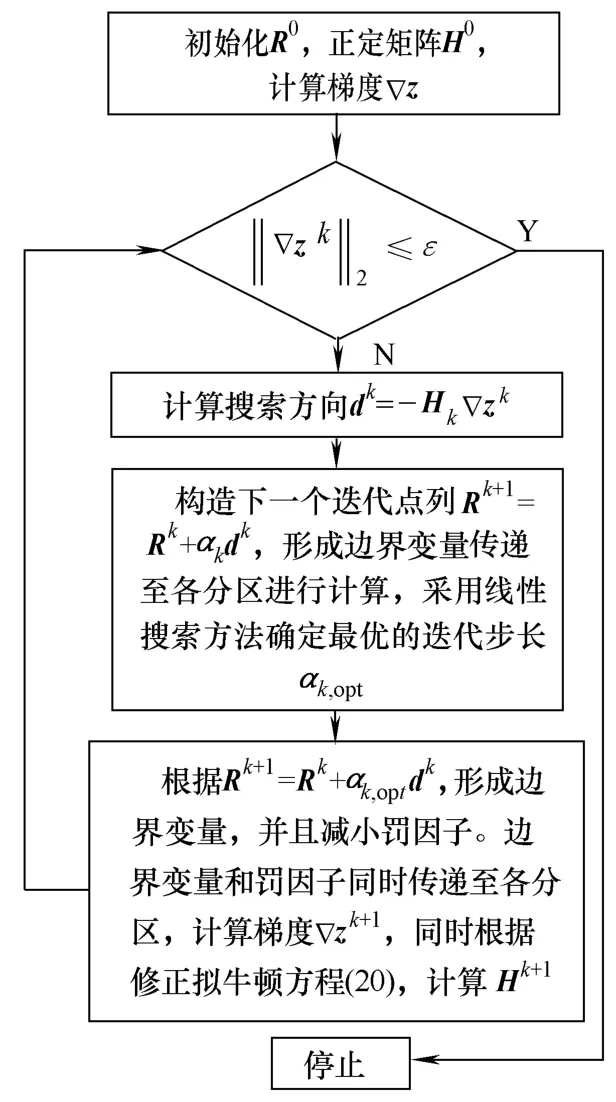
图3 区域协调中心算法流程Fig.3 Algorithm flow of area coordination center

在基于拟牛顿算法的计算流程中，需要获得每次迭代最优的搜索步长，由于模型（18）的目标函数是连续函数，采用多项式插值方法搜索的执行效率是最有效的，故本文采用直接三次内插的线性搜索方法。三次内插值方法利用函数估计和梯度组合确定三次函数的系数，从而确定最小极 值 ， 具 体 求 解 公 式 如 下 ， f(α1)、 f(α2)和∇f()、 ∇f ()分别表示α1、α2两点的函数值以及相应的梯度。

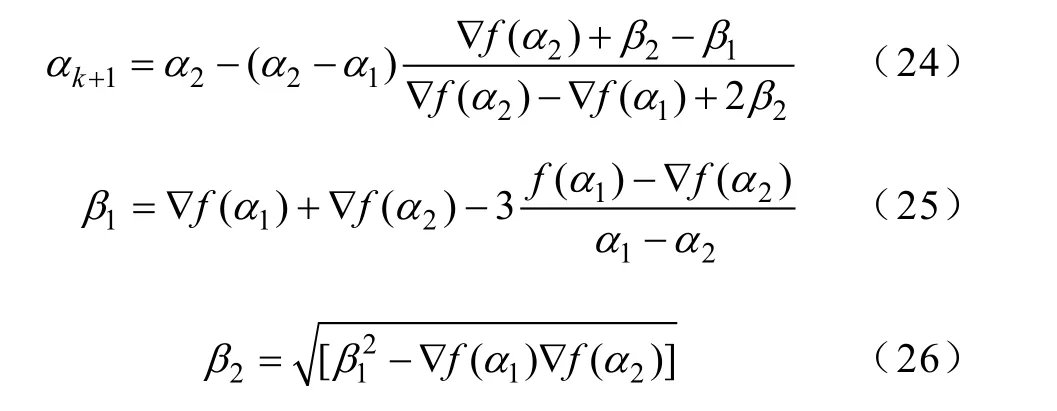
4.2 求解分区经济调度的原对偶内点算法

原对偶内点算法基于对数障碍函数方法，是一种多项式时间算法。其优点是具有对问题规模不敏感、数值鲁棒性强、计算精度高等特点。特别针对大规模的稀疏矩阵，能够采用矩阵分块技术，将大规模系数矩阵分块存储或约化，可明显提高算法的计算速度和效率[11]。鉴于原对偶内点算法的特点和优势，本文采用该算法求解分区内部经济调度。

4.3 层级协调整体算法流程

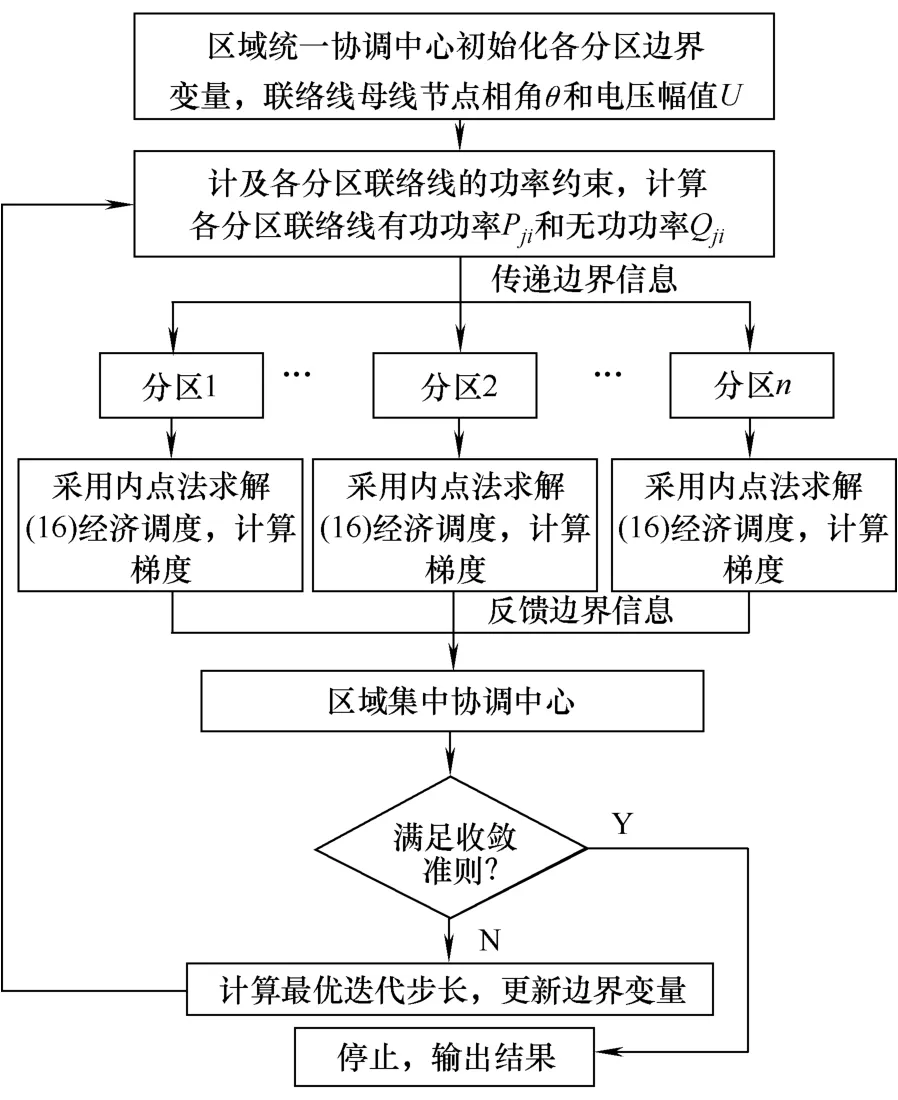
图4 层级协调整体算法流程Fig.4 Whole algorithm flow of hierarchy coordination

5 算例分析

5.1 算例描述

为验证本文所建模型和算法的有效性，本文采用IEEE30节点系统拓扑图求解互联电网经济调度，该系统共有6台发电机，41条线路。

由于不同分区方案将影响算法的执行效率，分区数目过多，需要协调的分区边界变量增多，将增加区域协调中心的协调难度，进而影响算法的收敛时间；而分区数目较少，各分区的电网规模仍然较大。因此，在权衡各方面因素之后，采用文献[12]的分区方案，分区之间的联络线情况如图5所示。

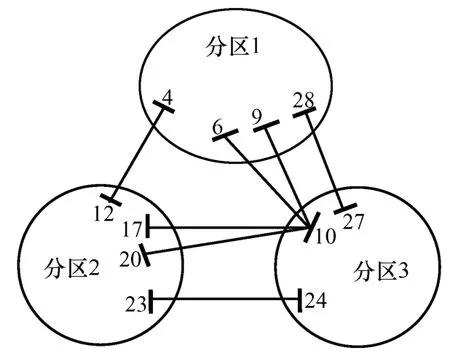
图5 IEEE30系统分区Fig.5 IEEE 30-bus interconnected systems

发电机发电费用函数采用二次曲线函数，具体参数信息见表1。

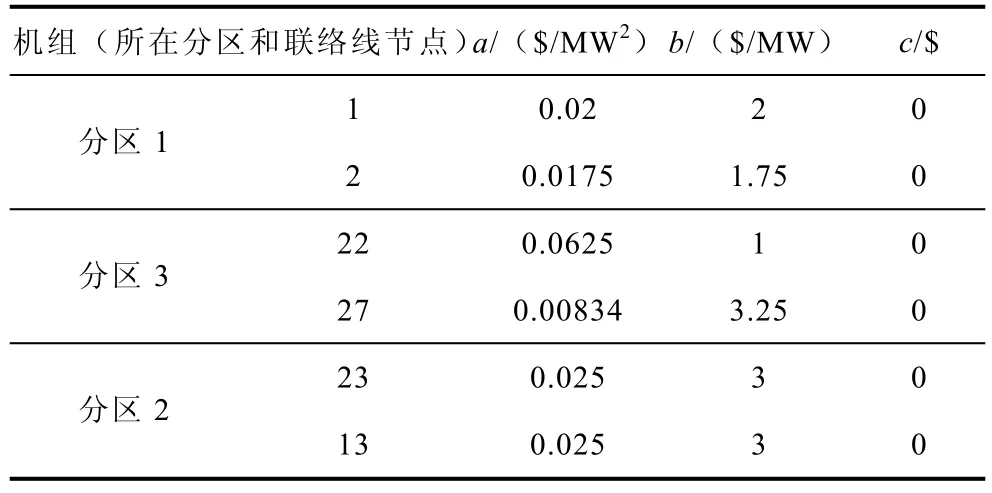
表1 发电费用的二次曲线参数Tab.1 Coefficients of generation cost quadratic curve

5.2 优化结果分析

采用平稳启动方法，各分区之间联络线初始潮流为零，区域协调中心传递至各分区的边界节点相角初值为零，电压幅值为1（标幺值）。区域协调中心和三个分区优化迭代过程如图6所示。

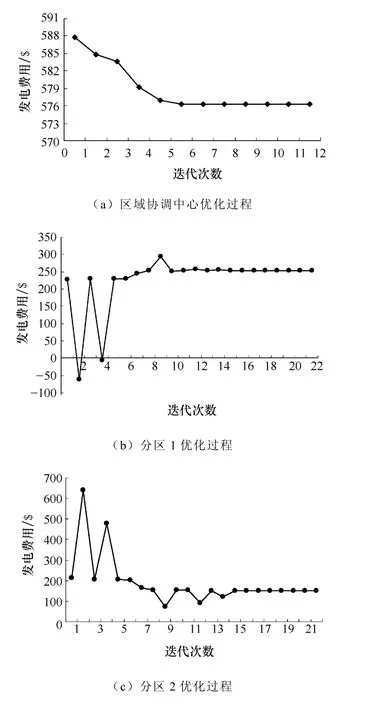
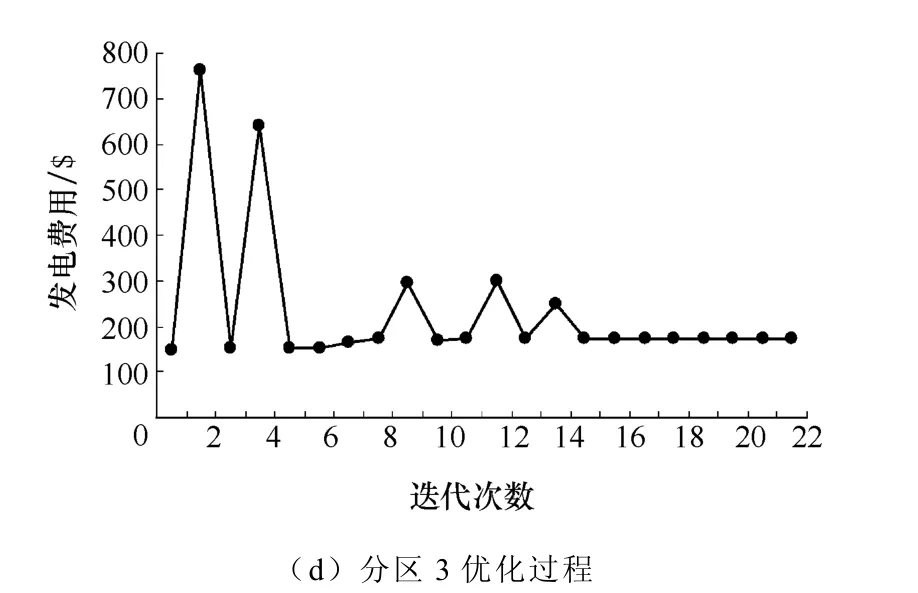
图6 区域协调中心和分区优化过程Fig.6 Optimal process of area center and sub-area

从图6优化过程分析，区域协调中心优化的目标函数值呈单调递减趋势，在前6次迭代中，区域协调中心优化的目标函数值下降幅度已经较明显。经过 12次迭代后，从初始值 587.75$最终收敛到576.82$。三个分区均在初始迭代过程中出现了振荡（主要是出现了不可行解的原因），随后均一致收敛。

为检验上述层级协调方法的优化效果，与全区域统一经济调度进行比对分析，仍采用原对偶内点算法对模型（1）进行全局优化计算，网络和发电机参数、负荷数据、边界变量初始值与层级协调方法一致，对比结果见表2。

表2 对比分析Tab.2 Comparative analysis

从表2可以看出，与全区域统一经济调度结果相比，本文提出的层级协调优化方法总发电费用为576.82$，优于全局优化方法。从迭代次数而言，全局优化需要迭代 19次；本文区域协调中心需要迭代 12次，各分区由于在某些迭代点的搜索方向上需要进行多次线性搜索寻优，整个优化过程需要迭代 22次，故本文优化方法计算时间要大于全局优化方法。

模拟分析区域协调中心进行联络线功率局部调控的情况。以调控联络线4-12的有功功率为例，在无调控情况下，最终功率从节点4流向节点12，现假设调控目标是使其潮流反向，优化结果如图7所示。

调控联络线 4-12功率方向将影响到最终优化结果，体现在：①最终联络线4-12的潮流为零，分区2无潮流流向分区1，原因是分区2单位发电成本要高于分区1；②区域协调中心经过13次迭代最终收敛到目标函数值586.85$，相比不调控情况有所提高。可见，施加局部调控后，整个优化结果发生了变化，体现了区域协调中心的调控目标。

图7 调控联络线4-12功率的优化过程Fig.7 Optimal process of controlling tie-line 4-12

6 结论

本文提出了一种求解互联电网经济调度的层级协调方法。该方法基于层级调度的协调运作机制，通过协调边界变量对互联电网经济调度模型进行重构，再基于二次罚函数法将边界变量约束松弛进入各分区目标函数中，构建了分区和区域协调中心各自的优化模型，并提出了拟牛顿算法和原对偶内点算法进行求解，从而实现了各分区之间的解耦和层级协调运作。IEEE30节点算例表明，本文求解方法能够很好地收敛，优化效果较佳，无调控情况下其优化结果优于全区域统一经济调度。施加调控后的计算结果则能够体现区域协调中心的决策意愿，方便实现一对多的全局控制目标。

本文需要进一步提高整个优化的计算速度，解决该问题的方法，例如进行分布式并行计算、实施有效的分区方案等，这尚需要展开进一步深入研究。

[1]Bakirtzis A G, Biskas P N. A decentralized solution to the DC-OPF of interconnected power systems[J].IEEE Transactions on Power System, 2003, 18(3)：1007-1013.

[2]刘科研, 盛万兴, 李运华. 互联电网的直流最优潮流分解算法研究[J]. 中国电机工程学报, 2006, 26(12)： 21-25.Liu Keyan, Sheng Wanxing, Li Yunhua. Research on decomposition algorithm of DC optimal power flow in large scale interconnection power grids[J].Proceedings of the CSEE, 2006, 26(12)： 21-25.

[3]Kim B H, Baldick R. Coarse-grained distributed optimal power flow[J]. IEEE Transactions on Power Systems, 1997, 12(2)： 932-939.

[4]Baldick R, Kim B H, Chase C, et al. A fast distributed implementation of optimal power flow[J]. IEEE Transactions on Power Systems, 1999, 14(3)： 858-864.

[5]王兴, 宋永华, 卢强. 多区域输电阻塞管理的拉格朗日松弛分解算法[J]. 电力系统自动化, 2002, 26(13)： 8-13.Wang Xing, Song Yonghua, Lu Qiang. Lagrangian relaxation based multi-region transmission congestion management[J]. Automation of Electric Power Systems, 2002, 26(13)：8-13.

[6]Wang Xing, Song Yonghua, Lu Qiang. Lagrangian decomposition approach to active power congestion management across interconnected regions[J]. IEE Proceedings on Generation, Transmission and Distribution, 2001, 148 (5)： 497-503.

[7]Liang M, Ali A. A decomposition method for multi-area OPF problem[C]. IEEE Power Systems Conference and Exposition, 2006： 1689 -1693.

[8]程新功, 厉吉文, 曹立霞, 等. 基于电网分区的多目标分布式并行无功优化研究[J]. 中国电机工程学报, 2003, 23(10)： 109-113.Cheng Xingong, Li Jiwen, Cao Lixia, et al. Multiobjective distributed parallel reactive power optimization based on sub-area division of the power system[J]. Proceedings of the CSEE, 2003, 23(10)： 109-113.

[9]刘宝英, 杨仁刚. 采用辅助问题原理的多分区并行无功优化算法[J]. 中国电机工程学报, 2009, 29(7)：47-51.Liu Baoying, Yang Rengang. Muti-subarea parallel reactive power optimization based on APP[J]. Proceedings of the CSEE, 2009, 29(7)：47-51.

[10]黄红选, 韩继业. 数学规划[M]. 北京： 清华大学出版社, 2006.

[11]Xie K, Song Y H. Power market oriented optimal power flow via an interior point method[J]. IEE Proceedings on Generation, Transmission and Distribution, 2001, 148(6)： 549-556.

[12]黄海涛, 郑华, 张粒子. 基于改进粒子群算法的可用输电能力研究[J]. 中国电机工程学报, 2006, 26(20)： 45-49.Huang Haitao, Zheng Hua, Zhang Lizi. Study of available transfer capability based on improved particle swarm optimization[J]. Proceedings of the CSEE, 2006, 26(20)： 45-49.