一种基于分布式电源的串联补偿方式的设计

李勇汇 吕艳萍 彭 辉 朱海昱

（1. 武汉大学电气工程学院 武汉 430072 2. 武汉国测科技股份有限公司 武汉 430223）

1 引言

常规电厂一般都远离负荷中心，它们产生的电能需要通过长距离的输/配电网才可以送到终端负荷。为了满足不断增长的负荷需求，电力系统必须投入大量的资金对输/配电网不断地加以更新和改造。如果电网的发展相对滞后于负荷的增长，则供电的可靠性就会下降。另外，传统的化石燃料电厂在生产电能时会产生大量的温室气体，给人类的生存环境造成严重影响。

基于上述原因以及传统能源资源的逐渐枯竭，以风能、太阳能和燃料电池为代表的可再生清洁能源正得到各国政府和电力部门的广泛重视[1]。通常，这些分布式电源（Distributed Generator, DG）离负荷较近、容量在 10kW～10MW 之间。传统的配电网系统在引入 DG后将会带来正反两个方面的影响[2]。一方面，DG可以降低配电网中的功率传输损耗、推迟线路的增容改造时间；另一方面，DG会带来诸如短路电流、电压调节、保护配合、谐波污染等新的问题。目前，DG的成本依然很高，很多相关技术还有待完善。研究和应用可靠性高、价格合适、高质量的分布式发电技术已经成为电力工业发展的重要课题。

DG接入配电网会直接影响到电力系统末端的负荷[3]。一个现代电力系统通常存在大量的敏感负荷，如医院、银行、芯片生产厂、空中交通控制中心等。这些负荷都需要高质量、不间断的电能供应。频率波动、谐波和电压暂降等电能质量问题将会直接造成生产和设备的巨大损失甚至是人身的伤害。提高负荷的电能质量，最大限度地利用DG是未来配电网设计中必须考虑的。

为了扩展DG的应用，文献[4]曾以燃料电池电源为核心提出了一种电能质量控制中心。在该中心的公共耦合点（Point of Common Coupling, PCC）上接有两种等级不同的负荷：一种负荷等级低，在上游系统发生电压暂降时将马上切除；另一种负荷等级较高，必须尽可能地保证供电不受影响。该文认为，高等级负荷可以耐受的电压暂降是非常有限的。当上游电源电压幅值突然下降超过20%时，电能质量控制中心必须切除低等级负荷并与上游系统解列。发生电压暂降后，处于孤立系统中的高等级负荷将以最低可以承受的电压水平运行。显然，文献[4]提出的改善配电网负荷耐受电压暂降能力的方案是不能令人满意的。同时该方案将带来诸如解列后同期、励磁涌流等多方面的问题。本文将以文献[4]的工作为基础，提出进一步改进配电网负荷耐受电压暂降的方案，合理扩大DG的应用范围。

2 DG在配电网中的稳态运行分析

为了清楚地认识DG在配电网中的作用，本文将以一个简化的配电网为例进行讨论。在图1所示的配电网中有两种不同等级的负荷：一种为等级低的普通负荷，功率为PL+jQL；另一种为等级高的敏感负荷，功率为PH+jQH。通常这两种负荷的有功功率满足PL＞PH。两种负荷同时由上游电源和DG供电。DG的有功输出只能满足部分高等级负荷。在发生电压暂降时，快速开关“C”可以迅速地切除普通负荷[4]。上游电源和DG分别通过等效电抗Xs和 Xf接在 PCC上，传输电阻忽略不计。根据典型配电网的短路容量，通常Xf至少是Xs的10倍。本文中的所有公式均采用标幺值。

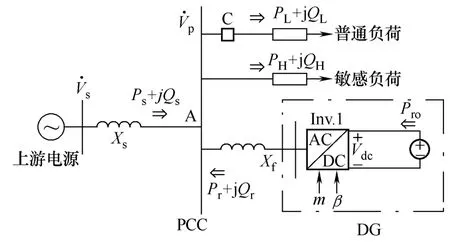
图1 含有DG的配电网示意图Fig.1 Illustration of a distribution network embedding with DG

风能、太阳能和燃料电池等类型的DG通常需要通过DC/AC能量转换装置接入交流系统。对于中小型DG（<1MW），图1中变流器（Inv.1）采用的电力电子器件一般为绝缘栅双极晶体管（IGBT）,以正弦波脉宽调制方法控制。图1中DG的直流输出电压为 Vdc。在互联情况下，Inv.1可以通过占空比m和相移角β 两个控制变量来调节配电网中的潮流分布[5]。通常 DG的动态响应速度较慢，无法像常规发电机一样在几秒内迅速地改变有功输出。因此，在实际应用中DG更适合追踪变化缓慢的负荷。另外，DG中电力电子设备的典型动作时间为µs级，因此图1中的DG可以快速调节配电网中的无功功率。通过合理调节DG输出的有功和无功功率，部分负荷可以就地满足，系统等效电抗Xs上的电压损耗将会减少，上游电源有功功率的传输能力将得以提高。

如果Inv.1的设计容量能保证在转换DG输出有功功率的同时还可以提供所有的负荷无功功率QL+QH，那么图1中A点的功率因数将维持在1。此时若选择PCC的电压pV˙为参考相量，上游电源注入到PCC的有功和无功功率将分别为

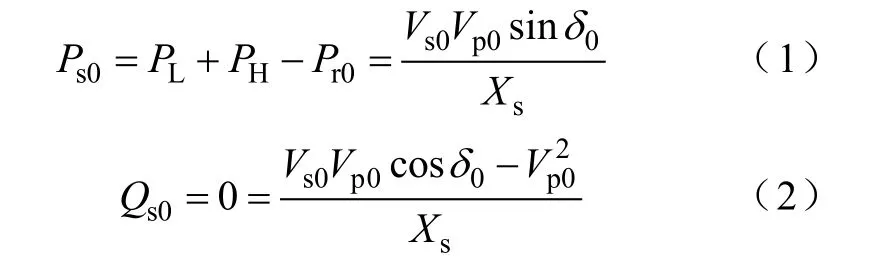
式中，下标“0”代表变量的初始值；Pr0是 DG的初始输出有功；Vs0、Vp0、δ0分别是上游电源、PCC母线的初始电压及两个电压之间的相位差。图1中p0V˙和负荷电压LV˙相同。

对式（1）和式（2）两式进行简化，可以得出式（3）和式（4）表明 Vs、Vp、Ps和δ 这 4个变量中仅有两个是独立的。若Ps和Vs为已知，则Vp和δ可求。具体的潮流控制方法参见文献[4]。

当上游电源因为短路或者大型电动机起动而发生电压暂降后，DG可以作为并联补偿器通过增加注入无功功率的方式抵消 Vs的下降、维持 PCC的电压不变。然而，如文献[6]中指出，这种并联补偿方式需要将 Inv.1的容量设计得远大于被保护的负荷容量。过高设计 Inv.1的容量作为无功备用是不经济的。同时，DG在并联补偿时所产生的无功电流会反向注入到上游电源，给上游电源保护配合造成困难。因此，国外很多电力部门都要求DG在上游电源发生故障时与系统解列[1]。为了更好地利用DG，提高负荷在电压暂降时的耐受能力，保证负荷的电能质量，本文提出了一种基于DG的新型串联补偿方式。

3 新型串联补偿方式的设计

系统发生电压暂降时，一般其持续时间约为0.5个周波到1s，电压幅值约为额定值的10%～90%，电压相角跳变的范围为-20°～20°[7]。加装串联补偿器（Series Compensator, SC）是抑制电压暂降、提高负荷电能质量最为有效的方法。SC串联在被保护负荷的上游，在检测到电压暂降后会向电路中注入串联电压，维持负荷的电压水平。注入串联电压的方式有三种[7-8]：分别是故障前注入法（pre-sag injection）、同相注入法（in-phase injection）和最小能量注入法（mini-mum energy injection），三种方法各有优缺点。不论采用哪种电压注入方法，负荷的耐受能力取决于 SC直流侧电容器中储藏的能量。当电压暂降持续时间、电压幅值下降超过一定范围时，负荷母线的电压将随着电容器中能量的消耗而下降，因此工程界一直都在探索提高负荷耐受能力的方法。结合电压暂降的补偿方式，理论上常用的有经典控制[9]、空间矢量控制[10]、非线性鲁棒控制[11]等控制方法。其中空间矢量控制法在研究不对称电压暂降时还可以结合瞬时无功理论进行分析[12]。

以下将结合图1着重分析三相对称暂降的补偿原理。为了方便讨论，本文只研究电压暂降过程中的基波，谐波问题不在本文的讨论范围。SC补偿电压暂降的方式选为故障前注入法。

3.1 一种串并联补偿拓扑结构

比较图1和常用SC的结构可以发现，DG的变流器（Inv.1）和 SC的变流器（Inv.2）可以共享一条直流母线。图2给出了这种拓扑结构的示意图。这种拓扑结构有三个优点：①电力电子设备可以灵活地调节配电网中的潮流，使 SC在电压暂降时有不间断的能量补充；②DG在发生电压暂降后可以保持和上游电源联接，避免解列和同期带来的问题；③SC的直流侧和DG共享母线后可以节省一个直流电容器和安装空间。图2中的拓扑结构将并联和串联补偿结合在一起，可以视为一个小型的灵活输电装置。

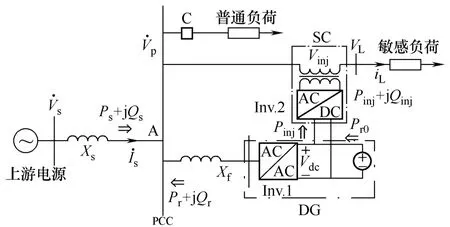
图2 共直流母线型SC示意图Fig.2 Illustration of a series compensator sharing a same DC-link with DG

在没有发生电压暂降时，图2中的串联补偿装置可以被旁路，DG的输出Pr0和并联支路Xf上流过的有功Pr相等。在发生电压暂降后，普通负荷将被迅速切除，同时串联补偿装置将投入运行并注入串联电压。此时在图2中，Pr0、Pr和串联补偿装置注入到负荷支路的有功 Pinj之间存在如下功率守恒关系

由于DG的动态响应速度较慢，在发生电压暂降前后可以假定其有功输出 Pr0不变。在发生电压暂降后，SC从电源吸收有功功率满足 Pinj＞0。如果 Pinj＜Pr0，DG 多余的有功功率仍从 Inv.1流向PCC。如果Pinj＞Pr0，DG的初始有功功率不足以抑制电压暂降，Inv.1将从PCC吸收有功，支路Xf上流过的有功功率反向。由此可见，SC在这种拓扑结构中能够以灵活的方式、不间断地得到能量。

值得强调的是，虽然式（3）中 Pr的方向会因为补偿程度的不同而发生变化，但是DG总可以利用Inv.1中的两个控制变量调节其注入到PCC的无功功率，使得图2中A点的功率因数始终维持在1，实现并联补偿。

3.2 SC容量的设计

3.2.1 拟稳态分析

如果感兴趣的仅是发生电压暂降后的稳态过程，而不计电路中的暂态过程，可以利用类似第 2节的方法对图2中的系统进行拟稳态分析。

当Vs1＜Vs0时，由式（6）知，图2中的系统只能通过增大δ1来维持Ps1。由式（7）知，此时PCC电压p1V˙的幅值小于上游电源电压并滞后δ1。当δ1＝π/4时，上游电源可以向下游负荷提供的有功功率达到极限。此时图2所示拓扑结构可以耐受的最低的电压暂降幅值为

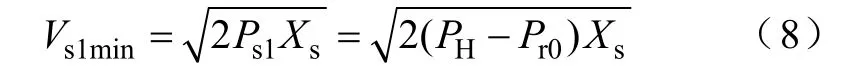
显然，只有当DG的有功输出恰好和敏感负荷的有功功率相等时，Vs1min才可以为零。

综合式（6）～式（8）可以发现，在考虑了DG的串/并联补偿作用后，图2中上游电源在发生电压暂降后电压幅值和相角允许的变化范围为

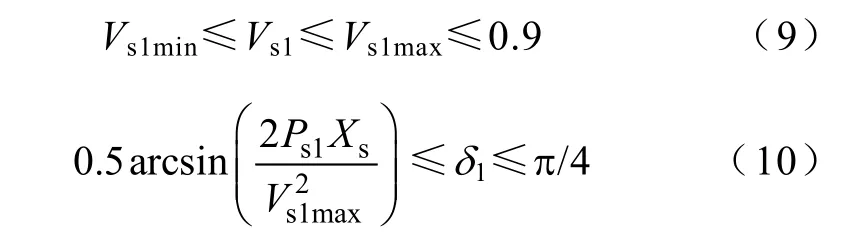
式（9）和式（10）也是图2拓扑结构在维持负荷电压幅值在故障前水平必须满足的运行限制。该限制是DG初始有功输出的函数。

3.2.2 SC容量和电压暂降幅值、相角跳变的关系图2系统中电压暂降发生前后的电压关系可由图3所示的相量图表示。通过相量图可以建立电压暂降的电压幅值Vs1，相角跳变αs和SC容量S之间的解析关系。

图3 电压暂降发生前后的相量图Fig.3 Phasor diagram before and after sag

在图3中，选取PCC在电压暂降前的电压相量为参考相量并记为（=）。和之间的夹角αs为相角跳变角。和之间的夹角为αp。发生电压暂降后，DG会分别调节图 2中 Inv.1和Inv.2的输出，使流过系统等效电抗 Xs的电流 I和同相，同时使敏感负荷的电压幅值维持在。此时，敏感负荷的视在功率SH、负荷电流和 SC的容量S之间满足

式中，injV˙是SC在电压暂降期间提供的注入电压。为方便起见，后面公式中S和SH两变量的绝对值符号将省略。

对图3中的△OAB，根据余弦定理，有

其中

将式（12）代入式（11），Vp1，αp和 S之间的关系如下：

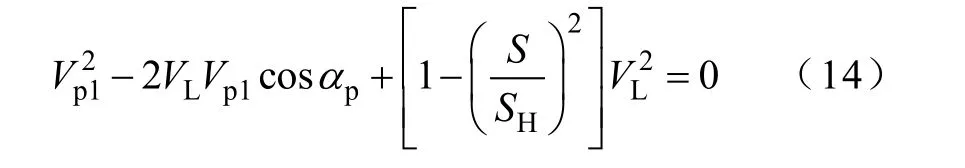
联立求解式（7）、式（13）和式（14），经推导（具体的推导过程见附录）后SC的容量S可表示为

显然，SC的容量和被保护负荷的容量成正比并且是反映电压暂降的变量Vs1和αs的函数。由于Vs1和αs在式（9）和式（10）给定的范围内变化，从理论上找出 SC所需的最大设计容量是可能的，也是非常必要的。

3.2.3 SC容量的讨论

从式（11）可以发现，对于SC的给定容量S，必存在一个反映补偿范围的圆Cs，如图4所示，该圆以B为圆心，以注入电压的幅值Vinj为半径。只有SC的容量设计得足以使图3中的A点落在圆Cs内，PCC母线电压p1V˙在经过补偿后才可以将负荷电压恢复到LV˙。

根据上游电源发生电压暂降时电压幅值和相角跳变可能的变化范围，图4给出了相应PCC母线电压可能的变化范围。当Vs1在式（9）给出的最大值Vs1max和最小值Vs1min之间变化时，由于稳态情况下电压幅值 Vs1和 Vp1间的关系始终满足式（7），弧P1P2和弧 P3P4分别为相应 PCC电压暂降幅值为最大（Vp1max）和最小（Vp1min）时的轨迹。从式（12）和式（13）可知，对于给定，当和之间夹角αp的绝对值为最大时（即αs取负的最大值时）Vinj将取极大值。图4中当PCC母线电压在可能的最大和最小幅值之间变化时，曲线P2P4为所有Vinj取极大值时的连线。为了能让 SC可以补偿所有可能范围内的电压暂降，必须从曲线 P2P4上找出一点使Vinj为最大值。从附录中的证明可知，曲线 P2P4上的P4点对应的Vinj为最大：即当上游电源电压幅值为最小值 Vs1min且相角跳变αs为负的最大值-αsmax时，SC所需的容量S为最大。考虑式（8）～式（10）和式（15），SC的设计容量Smax可以选择为

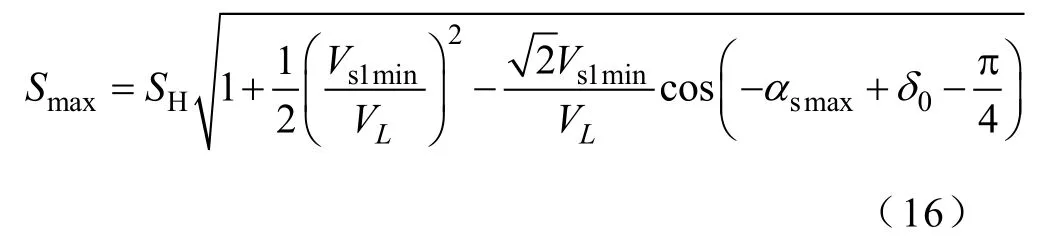
从式（16）可知，在给定图2系统初始参数后，可以方便地确定SC的容量。考虑到Vs1min＜VL且通常αsmax-δ0+π/4＜65°，可以从式（16）推知 SC的设计容量将小于被保护负荷的容量SH。

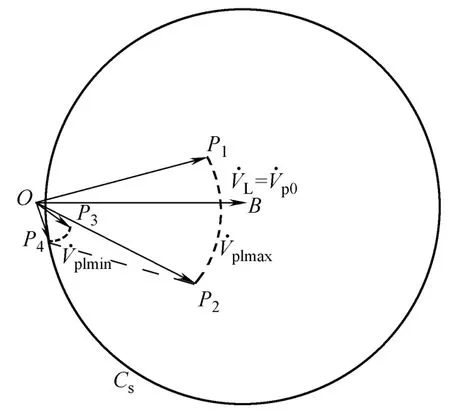
图4 SC补偿范围示意图Fig.4 Illustration of series compensation region

4 典型算例和仿真

本节将通过一个具体的算例来验证所提方案的可行性。

4.1 典型算例

与文献[4]一样，本文DG选择燃料电池，其额定有功功率和直流电压分别为100kW和330V。具体燃料电池参数和模型参见文献[13]。仿真交流系统的额定电压和额定频率分别为10kV和50Hz。两种不同等级的负荷均采用恒定阻抗模型。其中，普通负荷和敏感负荷的有功分别为2MW和500kW，功率因数均为0.9（滞后）。如果交、直流侧电压基准值分别为10kV和330V，功率基准值为500kVA，图2中相应系统参数的标幺值由下表给出。根据典型的配电网参数，假定上游系统电源和DG的短路容量分别为 100MVA和 10MVA。在稳态情况下，燃料电池的初始有功为0.2（pu）（100kW）。

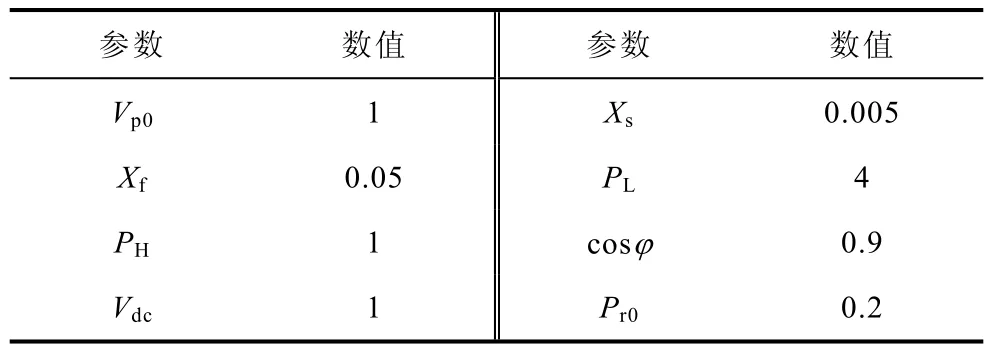
表 含有DG的典型配电网参数（标幺值）Tab. Parameters of a typical distribution network with DG（pu）

根据式（8）和表中的参数，可以确定图2系统可以耐受最低电压暂降的幅值约为0.09（pu）。由式（15）可计算出上游电源发生不同幅值和相角跳变时Vs1和SC容量S之间的关系，如图5所示。可以看出，随着上游电源电压幅值下降，SC所需的设计容量 S随之上升。在 Vs1为 0.09（pu）相角跳变为-20°时，SC所需容量为最大值，约为 1.08（pu）。这个容量小于被保护的高等级负荷容量1.11（pu）与式（16）的计算结果一致。因此可以选1.08（pu）（540kVA）作为SC的设计容量。

图5 不同相角跳变情况下SC容量和电压暂降幅值的关系Fig.5 The relationship between SC rating and sag magnitude under different phase jump angles

4.2 仿真结果

本文提出的串联补偿方式将在本节进一步通过Matlab/Simulink加以验证。仿真使用的参数见上表。为方便起见，图2中Inv.1和SC均采用理想元件并采用文献[5]中介绍的正弦波脉宽调制方法进行控制，电力电子器件产生的谐波忽略不计。从图5可知，图2中的上游系统电压发生50%电压暂降且相角跳变为0°时，SC维持负荷电压在故障前电压水平所需的容量约为0.56（pu）（280kVA）。假设电压暂降在0.05s发生，持续时间为30个周波，在0.07s时普通负荷被切除并投入SC。在电压暂降结束后1个周波，SC退出运行。具体的仿真结果如图6所示。

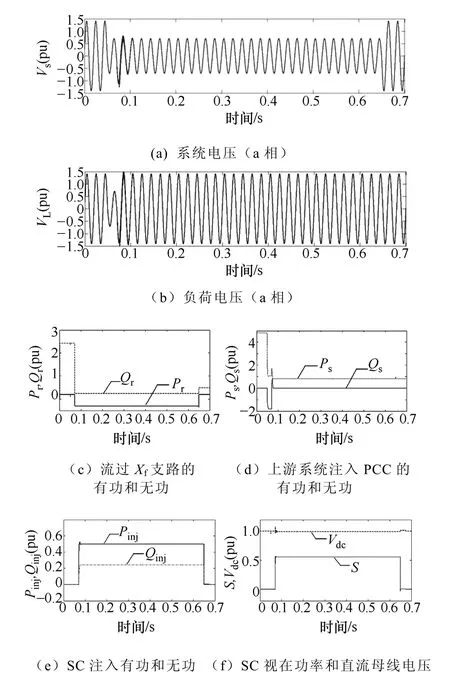
图6 系统发生50%电压暂降时的仿真结果Fig.6 Simulation results under a 50% voltage sag

从图6a和图6b可以发现敏感负荷的电压在经补偿后可以维持在1（pu）。在图6c中，DG中的Inv.1在系统没有发生电压暂降时向 PCC注入的有功功率为0.2（pu）。在发生电压暂降时，流过Xf的有功反向，Inv.1从系统吸收 0.3（pu）的有功功率。如图6d所示，由于Inv.1的调节作用，图2中A点的稳态功率因数始终为1。在发生电压暂降 1个周波后普通负荷被切除，上游系统提供给下游负荷的稳态有功功率为0.8（pu）。正如前文所设计的一样，Inv.1从上游系统吸收的有功和DG的有功同时提供给SC，用于维持负荷母线电压。在图6e中，SC注入负荷支路的有功 Pinj和两个电源提供的有功Pr+Pr0相等，为0.5（pu），在电压暂降期间，DG的有功输出维持恒定。图6f反映电压暂降期间直流母线电压近似恒定，且在 SC向负荷提供有功和无功功率时，SC的容量和式（15）计算值0.56（pu）近似相等，并小于其设计容量1.08（pu）。从仿真结果可以看出，SC确实提高了负荷耐受电压暂降能力。

5 结论

本文提出了一种基于DG的串联补偿方式。由于SC和DG共享直流母线，SC可以不断地从两个电源吸收有功功率，使得负荷耐受长时间、低幅值电压暂降的能力显著提高。本文提出的解析表达式给出了电压暂降时电压幅值、相角跳变和 SC容量之间的关系，为设计 SC时的容量确定提供了理论依据。仿真结果也进一步验证了所提方案的有效性。在未来的配电网设计中，可以参考本文提出的串联补偿方案，充分地利用DG的特点，在电压暂降发生时，灵活地调整系统的有功分布，保证负荷母线上的电压质量，向负荷提供可靠、经济的电能。今后，将对本文所提补偿方式的控制器设计具体方案进一步的完善。

附 录

1. SC容量解析表达式的详细推导

利用三角函数关系，式（15）可以写成

考虑到

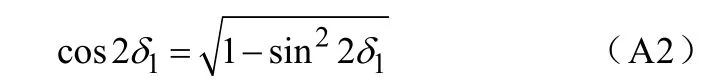
由式（6）有

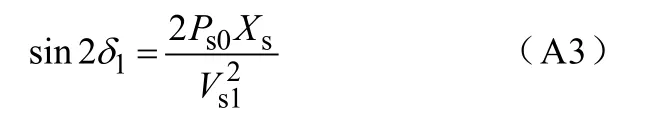
把式（A2）和式（A3）代入式（A1），SC的容量S和电压暂降幅值Vs1、相角跳变αs的解析表达式可写成

2. SC最大注入电压的讨论

根据式（7），式（12）和式（13），定义函数f

很显然，讨论函数f的增减性可以发现SC注入电压幅值Vinj的变化规律。

将式（A2）和式（A3）代入式（A5），对式（A5）求导，得

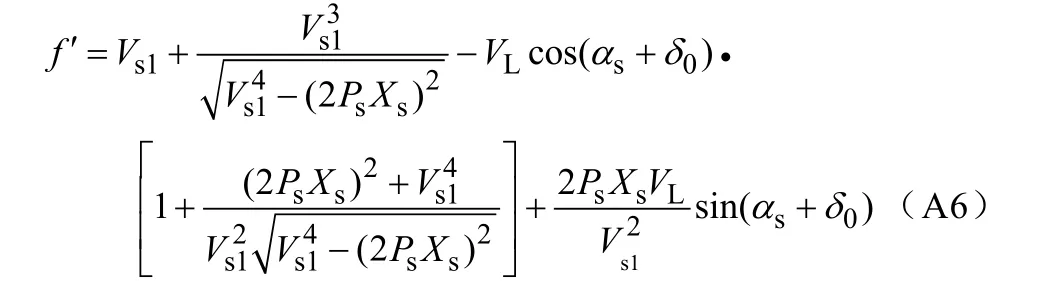
把式（A2）和式（A3）代入式（A6），式（A6）可以简化为

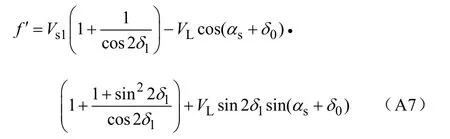
由3.2.3节的讨论知道，当αs=-αsmax时即在图4所示的曲线 P2P4上，Vinj将取得最大值。把αs=-αsmax代入式（A7），通常δ0都很小且满足|-αsmax|＞δ0，则 sin(-αsmax+δ0)＜0。由式（A3）知道，sin2δ1＞0。因此，式（A7）等式右边的第三项小于零。

考虑到典型的相角跳变满足-20°≤αs≤20°，这样有Vs1max≤ 0 .9VL＜ VLc os(-)，则式（A7）等式右边的第一项小于第二项，即有 f′＜0。这说明式（A5）定义的函数 f将是一个减函数，Vinj的值将随着 Vs1的增加而减少。因此，对应图4中的曲线P2P4，Vinj将在电压暂降幅值为最小且相角跳变为负的最大值时，即曲线P2P4上的P4点取得最大值。

[1]Jenkins N. Embedded generation[M]. London：Institution of Electrical Engineers, 2000.

[2]Ghosh A, Ledwich G. Power quality enhancement using custom power devices [M]. Newyork： Kluwer Academic Publishers, 2002.

[3]裴玮, 盛鹍, 孔力, 等. 分布式电源对配电网供电电压质量的影响与改善[J]. 中国电机工程学报,2008, 28(13)： 152-157.Pei Wei, Sheng Kun, Kong Li, et al. Impact and improvement of distributed generation on distribution network voltage quality [J]. Proceedings of the CSEE,2008, 28(13)： 152-157.

[4]Zhan Y Q, Li Y H, Choi S S, et al. The design of power quality control center to realize unbundled power quality supply[J]. IEEE Transactions on Power Delivery, 2006, 21(3)： 1421-1429.

[5]Mohan N, Undeland T M, Robbins W P. Power electronics： converters, applications, and design [M].New York： John Wiley & Sons, 2003.

[6]Weissbach R S, Karady G G, Farmer R G. Dynamic voltage compensation on distribution feeders using flywheel energy storage[J]. IEEE Transactions on Power Delivery, 1999, 14(2)： 465-471.

[7]Bollen M. Understanding power quality problems [M].New York： IEEE Press, 2000.

[8]Choi S S, Li B H, Vilathgamuwa D M. Dynamic voltage restoration with minimum energy injection[J].IEEE Transactions on Power Systems, 2000, 15(1)：51-57.

[9]Award H, Blaabjerg F. Transient performance improvement of static series compensator by double vector control[C]. Proceedings of l9th IEEE Applied Power Electronics Conference and Exposition, USA,2004： 607-613.

[10]Award H, Svensson J, Bollen M. Mitigation of unbalanced dip using static series compensator[J].IEEE Transactions on Power Electronics, 2004, 19(3)：837-846.

[11]Li Y W, Blaabjerg F, Vilathgamuwa D M, et al.Design and comparison of high performance stationary frame controller for DVR implementation[C]. IEEE App1ied Power Electronics Conference and Exposition, USA, 2006： 912-918.

[12]Lee S J, Kim H, Sul S K, et al. A novel control algorithm for static series compensators by use of PQR instantaneous power theory[J]. IEEE Transactions on Power Electronics, 2004, 19(3)： 813-827.

[13]Padullés J, Ault G W, Mc Donald J R. An integrated SOFC plant dynamic model for power systems simulation[J]. Journal of Power Sources, 2000,86(1-2)： 495-500.