一种基于EMD的短期风速多步预测方法

刘兴杰 米增强 杨奇逊 樊小伟

（1. 华北电力大学电气与电子工程学院 保定 071003 2. 承德供电公司 承德 067000）

1 引言

作为一种技术成熟、经济竞争力较强的可再生能源发电方式，风力发电日益受到重视并得到了长足的发展[1-2]。然而，风力发电具有“有风有电，无风无电”的间歇性特点，随着风电场规模的不断扩大，其间歇性问题日益突出，使接入电网的安全、稳定优质运行受到挑战，从而制约了风力发电的大力发展。因此，需要采取一定的手段来抑制或降低风力发电间歇性对电网造成的影响。研究表明，通过对风电场短期风速进行预测，继而由风电功率曲线得到风力发电输出功率的预测值是一种较为常用的方法[3]。而在实际运行中，提前多步对输出功率进行准确的预测，能够为电网调度部门实施调度控制、制定运行方式等提供有力支持，有效减轻风电波动对电网的影响，而且可以降低整个系统的运营成本[4]。因此，本文将对风电场的短期风速多步预测展开研究，以期得到更为准确的输出功率多步预测值。

风电场短期风速预测方法通常分为两类，即基于数值气象预报的风速预测和基于历史数据的风速预测。借助数值天气预报，预测时间可以达到24h、48h、72h甚至更长[5]。在我国，由于缺乏系统的风电场数值气象预报信息，大多采用基于历史数据的预测方法对风速进行预测[5]，比如持续预测法[6]、卡尔曼滤波法[7]、随机时间序列法[8]、人工神经网络法[9]、模糊逻辑法[10]以及一些组合方法[11]等。近来，有研究者提出一种滚动式时间序列法进行风速多步预测[12]，取得了一定的效果。然而，针对风速多步预测的专题报道较少，而且预测时都是针对风速原始序列进行的，预测时间偏短，当预测时间较长时预测精度偏低，无法满足电网调度运行的需要。我们知道，风速受到温度、气压、地形等多种因素的影响，包含着非常丰富的特征信息。通过对混杂多变的原始风速序列进行预处理，把具有相同或相近变化规律的特征信息提取出来，然后针对性地建立多步预测模型，将有望降低建模难度，提高多步预测精度。

经验模式分解(Empirical Mode Decomposition，EMD)是近年来出现的一种处理非线性、非平稳信号的新目标数据分析方法。相对于小波分析等信号处理方法，该方法不需要预先设定基函数，具有自适应性，因此克服了依赖预测人员主观经验的问题。另一方面，经EMD分解能够得到有限个基本模式分量（Intrinsic Mode Function，IMF），尽管有些IMF仍保持着不同程度的非平稳性，但是在它们之间的相互影响却被隔离开来，利用这种隔离可以尽可能地减小非平稳行为对预测的影响。同时，这些IMF能够突出原始数据的局部特征，有利于发掘数据内部蕴涵的变化规律。EMD已被证明在很多方面的应用效果皆优于其他信号处理方法[13-14]。

基于上述分析，本文首次将EMD方法应用在风电场短期风速的多步预测中，提出了一种基于EMD的风速多步预测方法。运用EMD技术对风速原始序列进行预处理，将其自适应地分解为一系列变化相对平稳的分量。之后，根据这些分量的变化规律，采用游程检验法将其重构为高-中-低三个分量，以提高预测效率。然后，针对性地建立各自的多步预测模型进行预测。最后，将三个分量的多步预测结果自适应叠加作为最终的预测风速。运用本文所提方法对某风电场实测风速序列进行了测试，结果表明运用该方法进行风速多步预测效果良好。

2 EMD简介

美籍华人Huang等于1996年提出了一种适用于非平稳时间信号的新分析方法，即Hilbert-Huang变换，该方法从根本上摆脱了傅里叶变换理论的束缚[14]。EMD是Hilbert-Huang变换的核心内容，其算法本质上是一个有限次的滤波过程。通过 EMD处理，被分析的时间信号分解为有限个IMF的组合，这些IMF信号具有如下两个特点：

（1）极值点（极大值和极小值）数目与跨零点数目相等或最多相差一个。

（2）由局部极大值构成的上包络和由局部极小值构成的下包络的平均值为零。

假定被分析的非平稳时间信号为 X(t)，根据IMF的含义，EMD的具体算法流程如图 1所示。

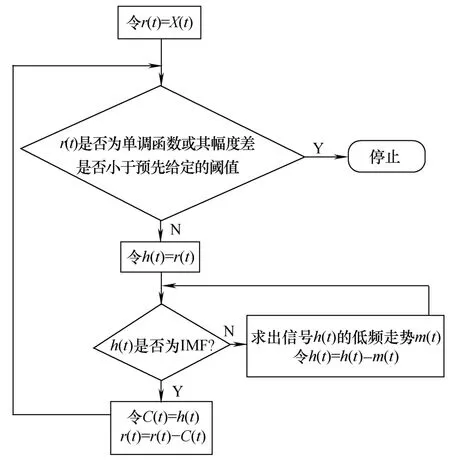
图1 EMD算法流程Fig.1 Flow chart of EMD algorithm

图中，r(t)为剩余分量，C(t)为分解得到的有限个IMF。停止迭代的阈值一般采用标准差Sd，如

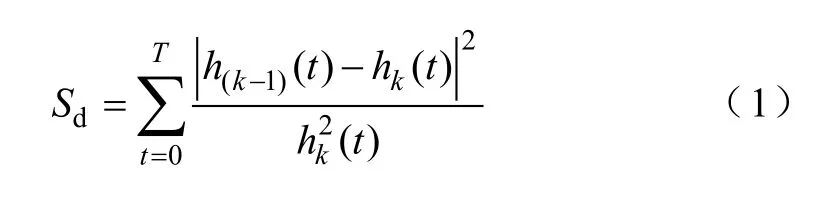
其典型值在0.2～0.3之间。

经上述过程，非平稳时间信号X（t）最终将被分解成n个IMF（标记为C1，C2，…，Cn）和一个剩余分量（标记为rn，该剩余分量可为一个平均趋势或常数），即

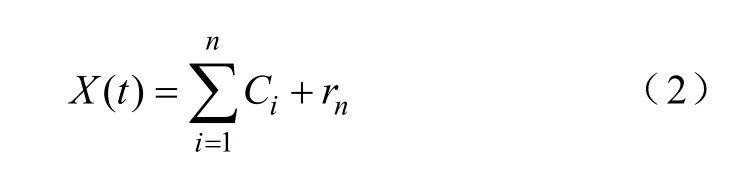
3 基于EMD的风电场短期风速多步预测模型

风速时间序列具有强非线性与非平稳性，因此采用常规的方法进行多步预测难以达到较好的效果。鉴于EMD技术在非平稳数据处理中的突出优势，本文提出了一种基于EMD的风电场短期风速多步预测新方法，其模型结构如图 2所示，主要包括EMD、重构、分类预测和自适应叠加四个模块。

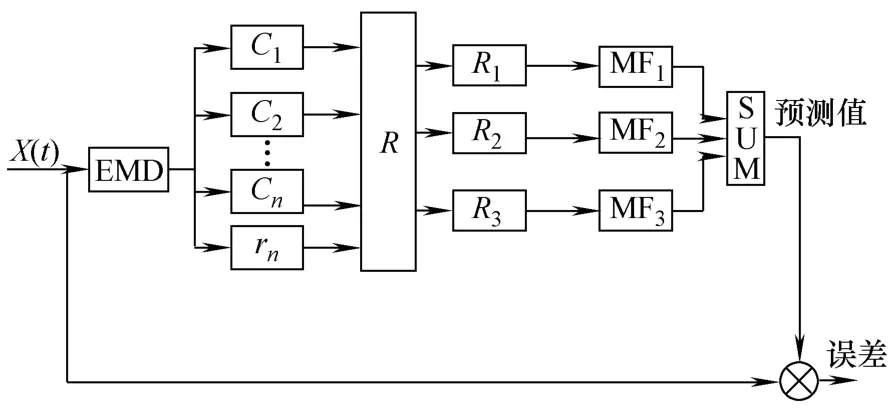
图2 多步预测模型结构Fig.2 The model structure of multi-step prediction

3.1 EMD

EMD的原理及具体算法见第2节所述。可见，通过 EMD处理可将原始时间序列分解为有限个IMF和剩余分量。这种分解不受主观因素的制约，并且在一定程度上将各分量之间的相互影响隔离开来，从而尽可能地减少了非平稳行为对预测结果的影响，有望提高多步预测精度。

3.2 重构

经EMD处理后，原始时间序列分解成为若干相对平稳的分量，然其平稳程度具有一定的差异且随着数据的变化自适应分解得到的分量个数不确定，这使得建模和预测难度加大。若能将平稳程度相近的分量进行重组，则不仅所包含的特征信息集中，而且使预测对象减少，从而可望在节约预测成本的前提下提高预测精度。文中选用游程判定法对分解所得的IMF和剩余分量进行波动程度的检验。游程判定法的原理如下[15]：

设某分量所对应的时间序列为{Y( t)} (t = 1,2,… , N)，均值为，比小的观察值记为“-”，比大的观察值记为“+”，如此可得到一个符号序列，其中，每段连续相同符号序列称为一个游程。可见，游程总数的大小反映了该分量的波动程度，故可根据游程数对分解所得分量进行分类，将其重构为高-中-低频三个分量。

3.3 分类预测

重构后的高-中-低频分量分别具有不同的变化规律，文中根据其特点分别采用不同的多步预测方法，以提高多步预测精度。支持向量机（Support Vector Machine，SVM）具有很好的泛化能力，并且具有全局最优解和较强的非线性处理能力[16]。有研究表明，SVM是目前针对小样本统计估计和预测学习的较好方法。由于高频分量变化较剧烈，其前后数据关联性不强，具有小样本的特点，故本文采用SVM对高频分量进行预测；对于变化较平稳的中频和低频分量，由于其具有随机特性，可以选择对随机过程描述较好的时间序列模型进行预测[17]。本文选择预测速度较快的AR模型，其参数确定可参照文献[18]。

3.4 自适应叠加

文中采用 GRNN[19]将高-中-低频分量的多步预测结果进行自适应叠加，通过在训练中动态修正各分量的权值，降低某些预测误差较大的分量对总预测结果的影响，以提高最终预测精度。

结合图 1，风速的多步预测过程可简述如下：首先，风速时间序列经EMD分解为 n个IMF，即Ci（i=1，2，…，n）和一个剩余分量rn；然后依据游程准则将这些分量重构为三个不同频率的分量（R1，R2，R3）；之后针对重构后各分量的特点，分别建立SVM模型和AR模型进行多步预测；最后采用GRNN将三分量的预测结果进行自适应叠加，得到最终的风速预测值。

4 算例及结果分析

以华北地区某风电场实测小时风速为例对所建模型进行了验证。原始风速时间序列（共720h，即 720个采样点）如图 3所示，其中，第 481～720采样点（后 240h）为测试样本。可见，该原始时间序列变化较剧烈且无明显规律可循。根据第 3节所述的多步预测过程，依次利用最近 480点，对测试样本进行了多步预测。例如，当提前6步预测时，则用第 1～480点预测第 481～486点，然后用第 7～486点预测第 487～492点，以此类推。

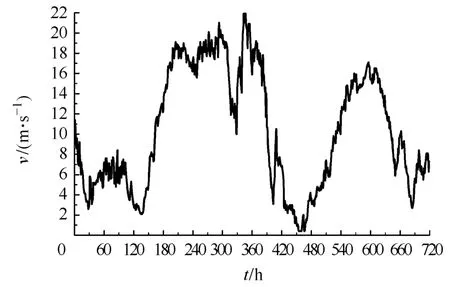
图3 原始风速时间序列Fig.3 The original wind speed time series

图4所示为第1～480个采样点的EMD结果。可见，该时间序列经EMD处理后共产生9个IMF（C1～C9）和一个剩余分量 r9。同时注意到，这些分量相对于原时间序列变化较为平稳。进一步地，按照3.2节方法计算这些分量的游程个数，结果见表 1。考虑到本文研究对象为小时分速，样本数 N为 480，则选择 n1=20作为高频分量的阈值（大于n1的为高频分量），而以剩余分量的游程数 n2作为低频分量的阈值（小于等于 n2的为低频分量），其余为中频分量。由此，将C1～C5叠加作为高频分量R1，C6～C9叠加作为中频分量 R2，r9作为低频分量R3，重构结果如图 5所示。显然，经重构后，原始时间序列成为频率从高到低排列且特征信息集中的三个分量。分别对三个分量进行多步预测，并将各预测结果自适应叠加作为最终预测风速。

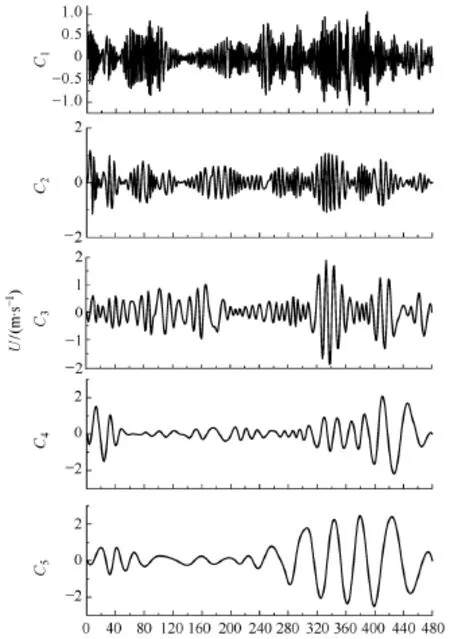
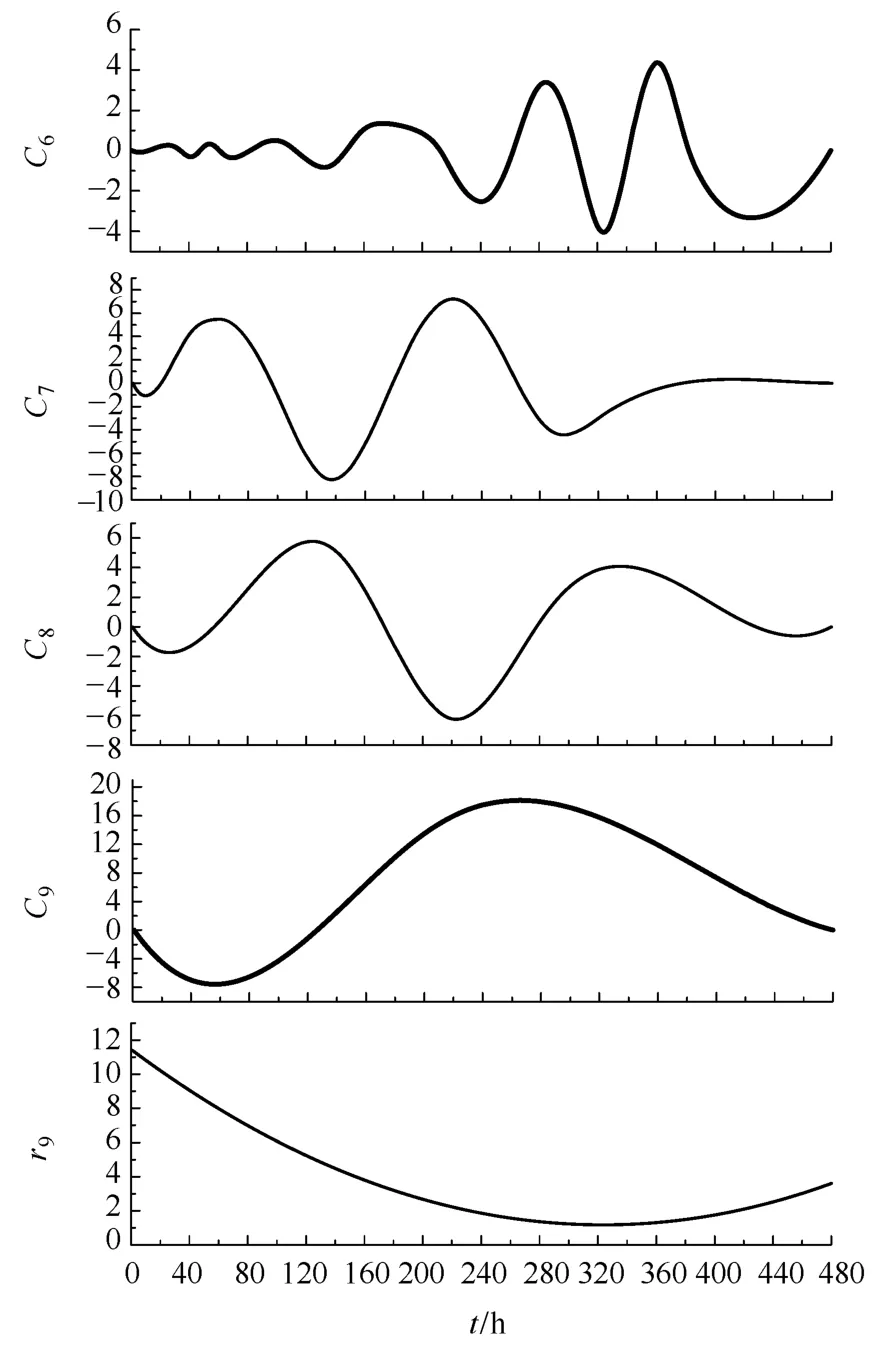
图4 采样点1～480的EMD结果Fig.4 The EMD results of wind speed time series

表1 各分量的游程总数Tab.1 The run-lengths of C1～C9 and r9

图6所示为提前6h的预测风速与实测风速的对比结果。同时，图中也给出了将重构所得分量的多步预测值直接叠加作为预测风速的仿真结果。观察图6可以发现：

（1）提前6h的风速预测值与实测值吻合较好，说明所建立的多步预测模型符合该风速的变化规律。

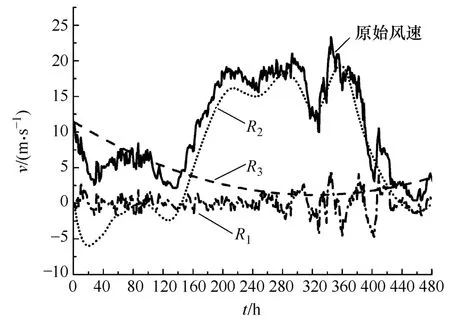
图5 重构结果Fig.5 The reconstruction components of wind speed time series

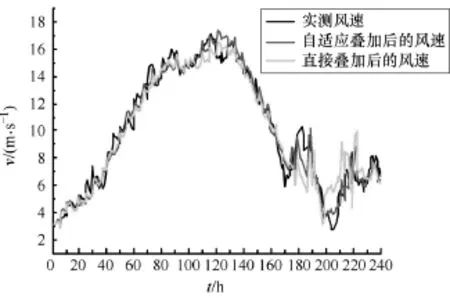
图6 预测风速与实测风速的对比Fig.6 The comparison of real wind speed and the prediction results

（2）经过自适应叠加的风速预测值在大多预测点较直接叠加的预测值更接近风速实测值，尤其在风速变化幅度较大的阶段（第 175～240点），表明通过将三个分量的多步预测值进行自适应叠加，能够在一定程度上提高风速多步预测的准确性。

为了进一步验证本文所提算法的有效性，分别采用 SVM 和 AR模型对该风速测试样本进行了预测，并对各算法的预测结果进行了误差分析，结果列于表 2中。分析表 2可知，当采用方均根误差（RMSE）或相对平均误差（RME）作为目标检验函数时，本文所提算法的多步预测精度较其他两种常规算法均有大幅提高。RMSE表示的是误差的统计学特性，反映的是样本的离散程度，而RME反映的是误差的整体情况。可见，采用本文算法不仅提高了多步预测的整体精度，而且保证了大多数预测点与实测风速的偏离程度较小。同时，通过进一步比较发现，对于同一种误差衡量指标，虽然其数值均随预测步长的增加而增大，但本文算法的误差增加幅度最小。因此，可以推断当进行更长时间的多步预测时，采用本文算法能够取得较好的预测效果。

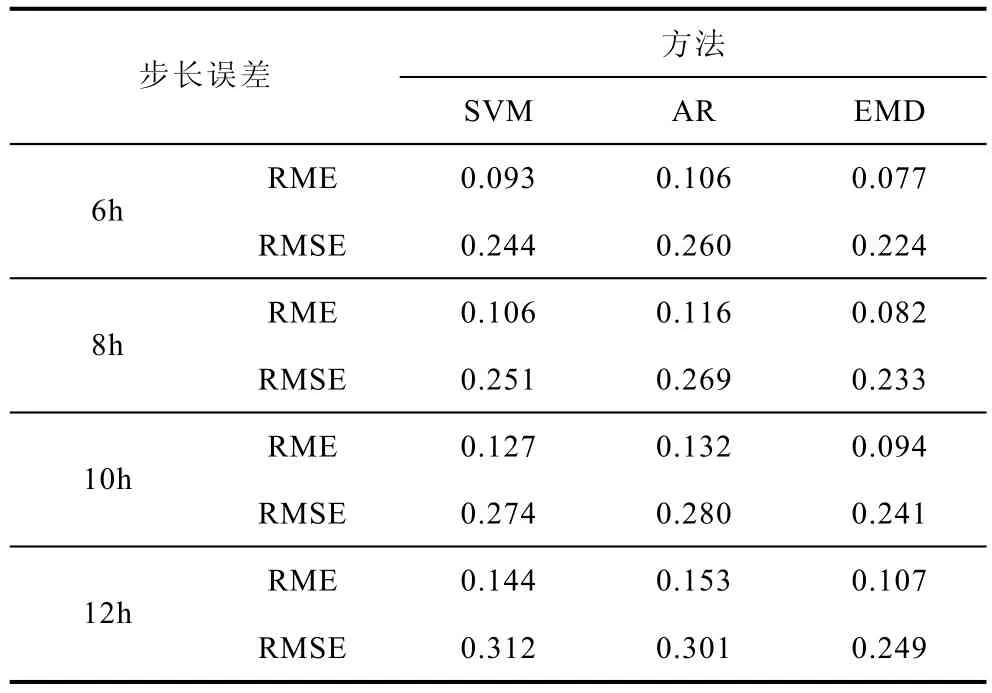
表2 不同方法的预测误差对比Tab.2 The errors of wind speed prediction with different methods

5 讨论

相对于直接采用SVM或时间序列法（AR模型），本文所提算法在进行多步预测时由于经EMD处理，风速时间序列被自适应地分解为一系列变化相对平稳的分量，从而在一定程度上降低了不同特征信息之间的干涉和耦合。而通过重构将那些变化规律相近的分量进行整合，将会使所得分量包含的特征信息集中且变化规律明显，进而能够有针对性地对三个分量分别建立较为准确的多步预测模型。这样在很大程度上解决了因EMD分解所得分量不确定而引起的建模难度大、建模不准等问题，进一步地，使多步预测的精度得以大幅提高。同时，重构处理使预测分量大大减少，从而提高了多步预测的效率。另外，由于本算法将重构后三分量的多步预测结果进行了自适应叠加，如此削减了个别预测偏差较大分量对总预测风速的影响，进一步提高了多步预测的精度。

6 结论

风速时间序列由于具有非平稳性和非线性，当进行多步预测时，其预测精度难以保证。为此，本文提出了一种基于 EMD的风电场短期风速多步预测新方法，并以某风电场实测小时风速为例对所建预测模型进行了验证。

（1）算例结果表明，运用本文方法不仅提高了风速多步预测的整体精度，而且保证了在大多数预测点的预测误差较小，尤其当进行更长时间的预测时，较SVM和AR等常规模型，本文方法的优势更为明显。

（2）风速时间序列经EMD处理后分解为若干相对平稳的分量，从而简化了不同特征信息之间的干涉和耦合，而重构后所得三分量特征信息集中且变化规律明显，进而能够有针对性地建立更为准确的多步预测模型，使多步预测精度得以大幅提高。同时，重构后分量大大减少，从而提高了多步预测效率，节约了预测成本。

（3）对重构所得三分量的多步预测结果进行自适应叠加，能够在一定程度上削减偏差较大分量对整体预测结果的影响，从而进一步提高了多步预测精度。

[1]World Wind Energy Association. Wind turbines generate more than 1% of the global electricity[EB/OL]. (2008-02-21)[2008-03-20]. http： //www.wwindea. Org.

[2]施鹏飞. 2007年中国风电场装机容量统计(征求意见稿). http： //cwea. org. cn.

[3]杨秀媛, 肖洋, 陈树勇. 风电场风速和发电功率预测研究[J]. 中国电机工程学报, 2005, 25(11)： 1-5.Yang Xiuyuan, Xiao Yang, Chen Shuyong. Wind speed and generated power forecasting in wind farm[J]. Proceedings of the CSEE, 2005, 25(11)： 1-5.

[4]刘永前, 韩爽, 胡永生. 风电场出力短期预报研究综述[J]. 现代电力, 2007, 24(90)： 6-11.Liu Yongqian, Han Shuang, Hu Yongsheng. Review on short-term wind power prediction[J]. Modern Electric Power, 2007, 24(90)： 6-11.

[5]韩爽. 风电场功率短期预测方法研究[D]. 北京： 华北电力大学, 2008.

[6]Alexiadis M, Dokopoulos P, Sahsamanoglou H, et al.Short-term forecasting of wind speed and related electrical power[J]. Solar Energy, 1998, 63(1)： 61-68.

[7]Bossanyi E A. Short-term wind prediction using Kalman filters[J]. Wind Engineering, 1985, 9(1)： 1-8.

[8]Torres J L, Garcia A, Blas M De, et al. Forecast of hourly average wind speed with arma models in Navarre(spain)[J]. Solar Energy, 2005, 79(1)： 65-77.

[9]Kariniotakis G, Stavrakis G, Nogaret E. Wind power forecasting using advanced neural network models[J].IEEE Trans. on Energy Conversion, 1996, 11(4)： 762-767.

[10]Damousis I G. Dokopoulos P. A fuzzy expert system for the forecasting of wind speed and power generation in wind farms[C]. 22nd IEEE Power Engineering Society International Conference, 2001,5(20-24)： 63-69.

[11]刘永前, 韩爽, 杨勇平, 等. 提前三小时风电机组出力组合预报研究[J]. 太阳能学报, 2007, 28(8)：839-843.Liu Yongqian, Han Shuang, Yang Yongping, et al.Study on combined prediction of three hours in advance for wind power generation[J]. Acta Energiae Solaris Sinica, 2007, 28(8)： 839-843.

[12]潘迪夫, 刘辉, 李燕飞. 风电场风速短期多步预测改进算法[J]. 中国电机工程学报, 2008, 28(26)： 87- 91.Pan Difu, Liu Hui, Li Yanfei. Optimization algorithm of short-term multi-step wind speed forecast[J].Proceedings of the CSEE, 2008, 28(26)： 87-91.

[13]杨培才, 周秀骥. 气候系统的非平稳行为和预测理论[J]. 气象学报, 2005, 63(5)： 556-570.Yang Peicai, Zhou Xiuji. On nonstationary behaviors and prediction theory of climate systems[J]. Acta Meteorologica Sinica, 2005, 63(5)： 556-570.

[14]Huang N E, Shen Z, Long S, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London Series A,1998, 454： 903-995.

[15]王振龙, 顾岚. 时间序列分析[M]. 北京： 中国统计出版社, 2000.

[16]林树宽, 杨玫, 乔建忠, 等. 一种非线性非平稳时间序列预测建模方法[J]. 东北大学学报(自然科学版), 2007, 28(3)： 325-328.Lin Shukuan, Yang Mei, Qiao Jianzhong, et al.Prediction modeling method for non-linear and non-stationary time series[J]. Journal of Northeastern University(Natural Science), 2007, 28(3)： 325-328.

[17]徐国祥. 统计预测与决策[M]. 上海： 上海财经大学出版社, 2001.

[18]杨位钦, 顾岚. 时间序列分析与动态数据建模[M].北京： 北京工业大学出版社, 1986.