舰船电力系统发电单元时域聚合方法

杨勇波 查晓明

(1. 武汉大学电气工程学院 武汉 430072 2. 湖北汽车工业学院电气工程系 十堰 442002)

1 引言

舰船电力系统的在线动态等值，可以提高战斗工况时电压稳定分析，优化暂态计算速度和系统控制，一直是船用电力系统研究的难点[1-2]。舰船电力系统中，发电机之间的电气距离较短，系统中的电压稳定为稳定分析的主要内容，且在舰船电力系统暂态过程中，多数电机功角被强制同调[3]。因此在舰船电力系统在线暂态分析中，大型互联电力系统中的基于同调概念的等值技术，在舰船电力系统中同样适用。与陆用系统相似，为简化计算，可以将受扰舰船电力系统划分为研究区域和外部区域[4-7]，然后用等值母线代替同调母线，再对同调的发电单元进行聚合获得外部系统的等值模型，这是系统分析时网络等值的一般步骤。在对同调发电单元进行聚合时，首先需要考虑结构保留，即使等值模型结构与原同调发电单元的物理模型的结构相同，有利于等值模型可以直接用于暂态稳定分析程序；其次要考虑模型参数的计算速度，有利于系统的在线分析的时效性。

传统的方法都在频率域对发电机进行聚合，需要进行参数拟合，故计算参数时需要进行迭代运算，因此在线计算耗时。文献[7]采用了加权平均和加权对数平均以及最小二乘，但存在适应性问题[8]。文献[9]的 SME方法仅考虑一台发电机的具体模型，其他发电机采用注入电流等效，这样等值系统精度不高。文献[8,10-11]为了等值模型有利于暂态计算，采用了结构保留的方法，考虑了发电单元的详细模型，提高了聚合精度，然而由于在频率域聚合，计算参数时采用了迭代运算，使计算耗时。文献[12-13]提出并发展了一种动态聚合技术，该技术采用了发电单元模型结构保留技术，考虑了发电机模型，励磁控制系统及原动机调速系统的详细模型，同时对发电单元进行聚合时采用了时域聚合方法，计算模型参数时采用了非迭代的代数计算，解决了在线分析的计算速度问题。然而该文发电机模型采用四阶模型，为了考虑暂态和次暂态在暂态系统分析中的作用，等值模型需要采用六阶发电机模型，并且励磁系统和调速器聚合方法可以进一步改进。本文提出的方法，发电机采用了更精细的六阶模型，励磁系统和调速系统聚合采用了线性加权原则。推导了基于六阶发电机模型的参数计算公式，给出了同调机与等值机参数和基值之间的关系，并给出了更详细控制系统的聚合步骤，可以方便实际应用。

该聚合方法首先聚合发电机母线，移除负荷。然后通过矩阵运算计算发电机电抗、时间常数、励磁系统和调速系统控制参数。发电机母线聚合考虑同调发电机终端母线变比，该变比同时影响励磁系统控制参数。

2 聚合公式推导

动态等值是以发电机同调、能量守恒和动态性能保持不变为基础的，故本部分的数学推导必须满足下面三个条件：

（1）所有同调机的转子速度相同。

（2）等值机的输出功率和同调机群输出功率之和相同。

（3）边界母线上的电压、电流保持不变。

2.1 发电机母线和网络化简[12-13]

为获得等值网络，首先要进行发电机母线和网络化简。假设原始网络的电压、电流可以表示成

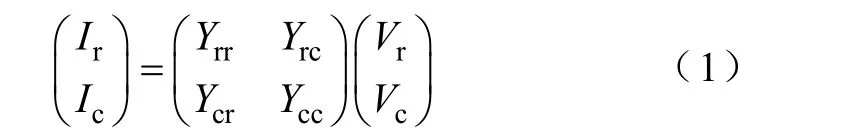
简化网络可以表示为

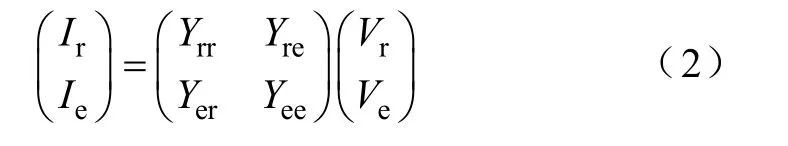
式中，下标r,c,e分别代表保留、同调、等值母线。由注入电流守恒可知，电压相量Vc，必须满足

如果定义同调母线电压为

等值母线电压为

则

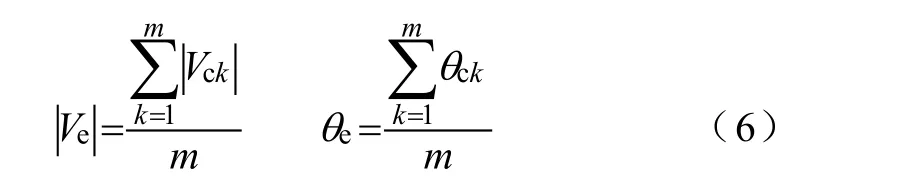
那么同调母线和等值母线之间的相移变换器表达式如

由式（3）和移相变压器表达式（7），可以得到研究区域和外部区域的自导纳和互导纳

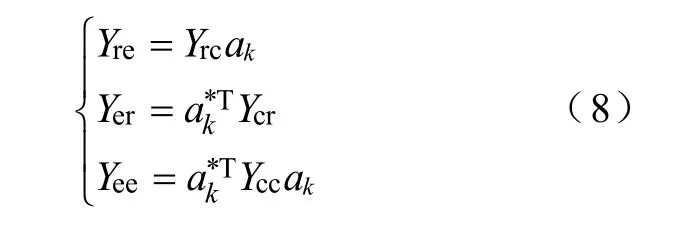
经过上述变换后，再通过静态等值，可以将原始网络简化为一个较小的等值网络。

2.2 发电机聚合

发电机常用模型，其最高模型阶数可达到八阶，本文建模时不考虑定子电磁暂态，考虑d轴的f、D绕组以及q轴的g、Q绕组的暂态和次暂态，以及转子机械动态，故为六阶[14-15]：

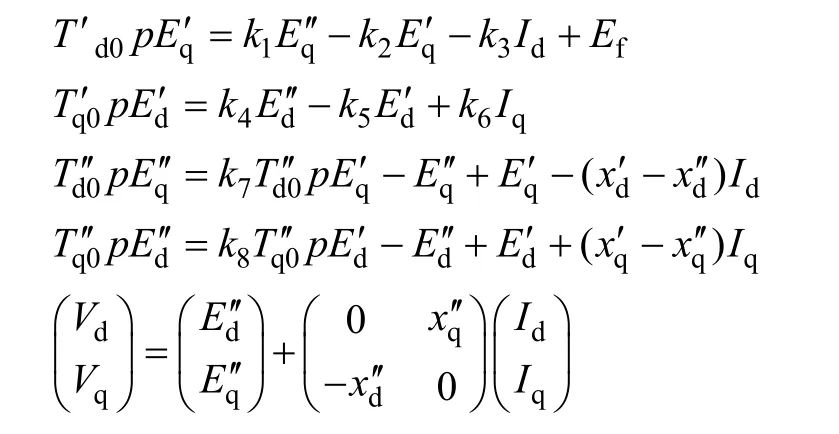
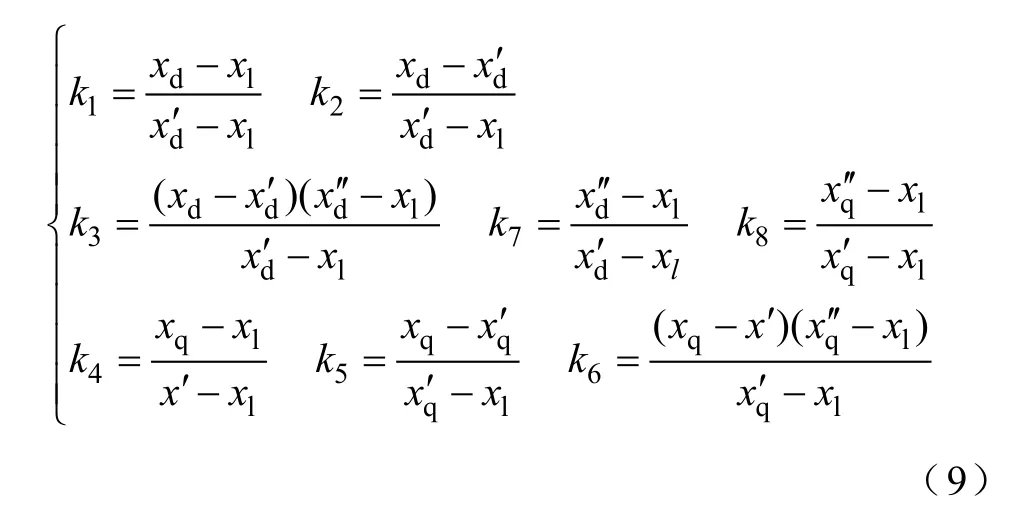
方程中的参数 k1～k8与同步电抗、暂态电抗和次暂态电抗有关，其获取细节可参考相关文献[14-15]。

2.2.1 电抗参数的获得

电抗参数包括同步电抗、暂态电抗、次同步电抗，为获得这些参数，在工程允许的误差范围内可以认为[14-15]

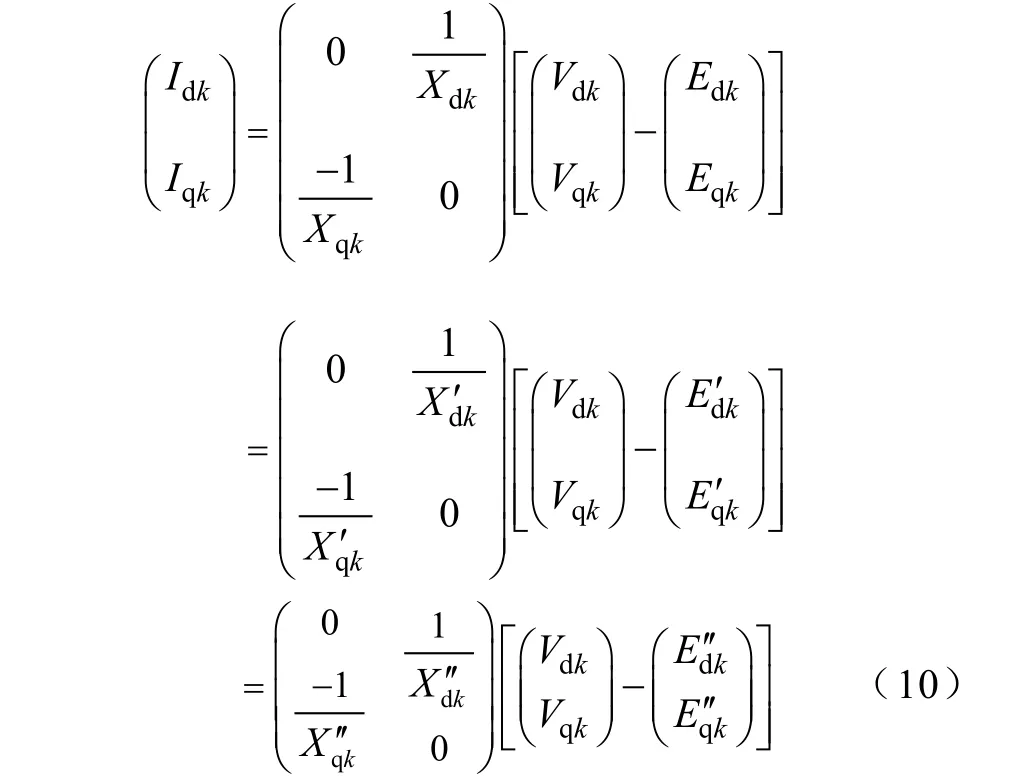
对同调机群，用符号表示有

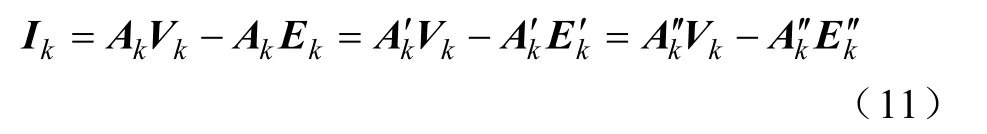
对于等值机可以得到同样形式的方程

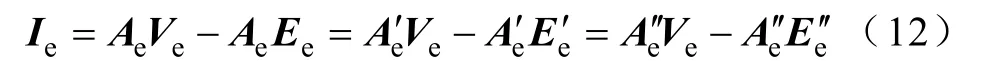
式中，Ae、、′和 Ak、、′拥有同样的结构。

根据边界电流不变的条件，在公共参考系（D，Q）中的等值机的电流，是所有同调机的电流注入之和，再根据各同调机和公共坐标系之间的关系可得

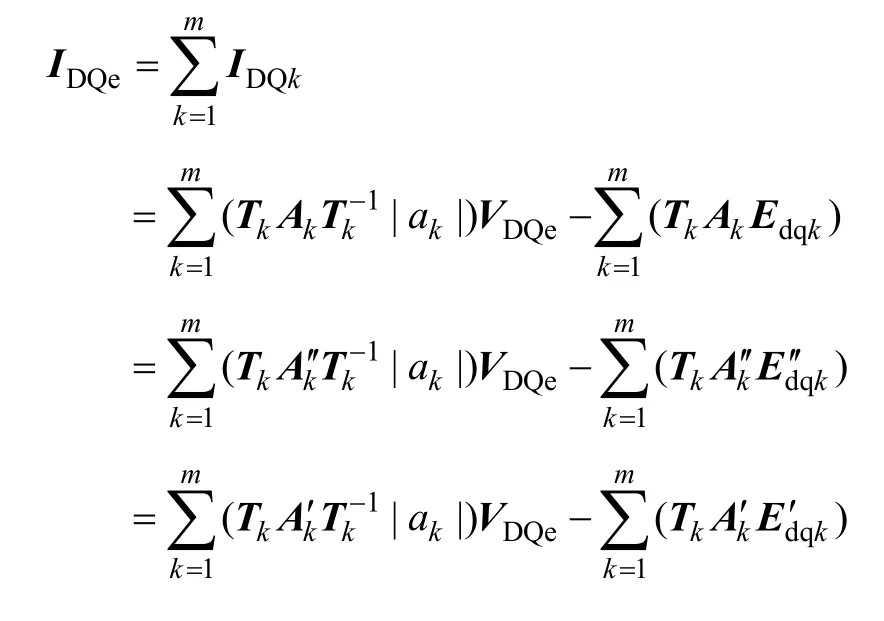
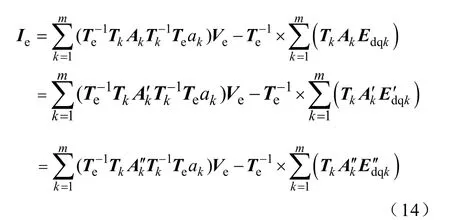
因此由等值机电流表达式（12）可得

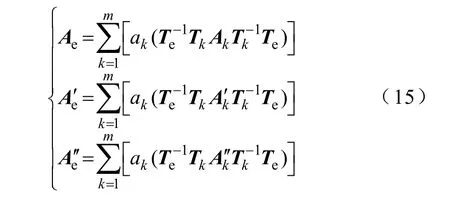
由等值机结构可得同步电抗、暂态电抗、次暂态电抗计算公式如下：

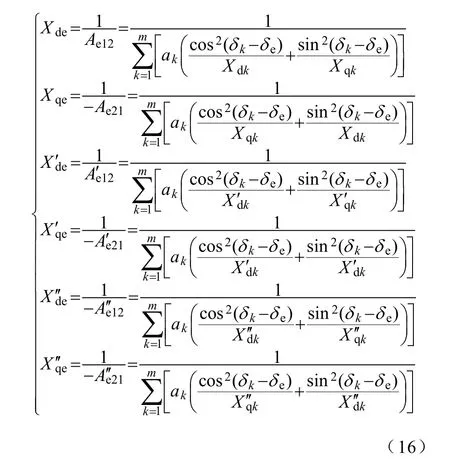
等值机电抗是δk-δe的函数，δk是同调机群转子角，其值可通过网络运行数据获得，δe是等值机转子角，其值为

等值机的漏抗可以通过加权平均获得

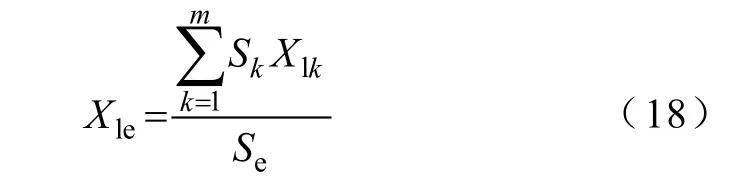
2.2.2 等值机惯性和阻尼常数估计

因为所有的同调机具有相同的速度偏差，同调机群的摇摆方程

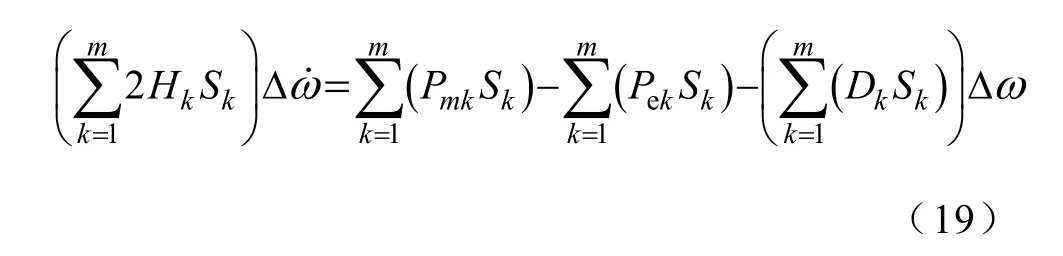
鉴于等值机的基值和容量是同调机群系统MVA容量之和，等值机参数表达为

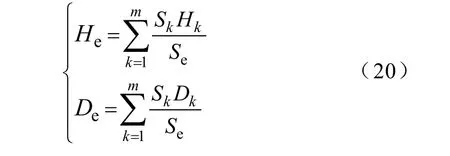
式中，Sk, Se分别为同调机群的容量和等值机容量。

2.2.3 时间常数的计算

为获得暂态时间常数，根据经验，在工程允许的误差范围内进行了一定的假定，即式（21）在一定条件下成立[14-15]：

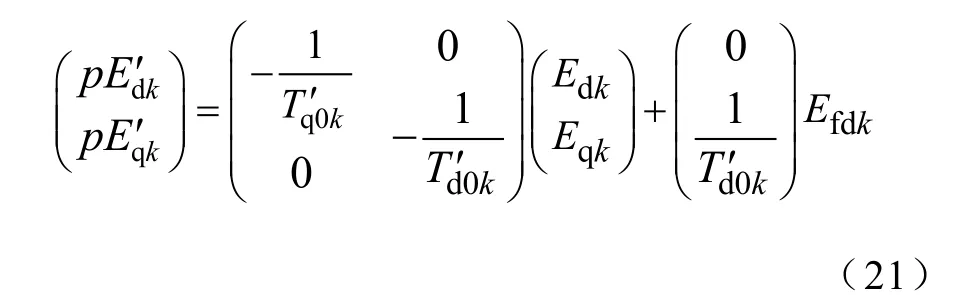
写成更简洁的形式可得

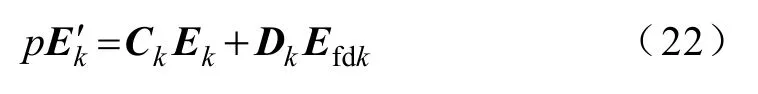
同样由式（9），对次暂态电势表达式，不做任何简化可得与式（22）相似结构的符号表达式为

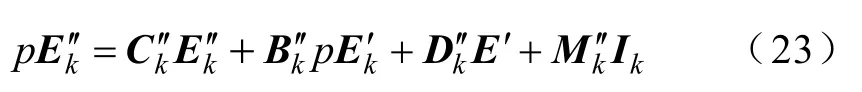
式中

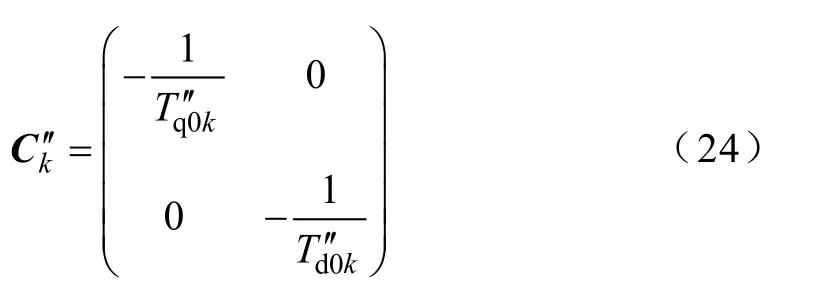
从而可得具有相同结构的等值机方程为

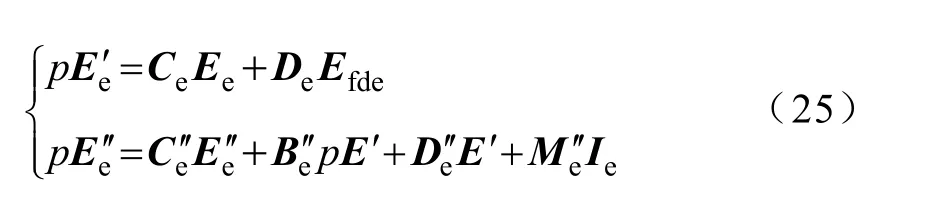
对式（12）和式（14）进行对应项比较可得

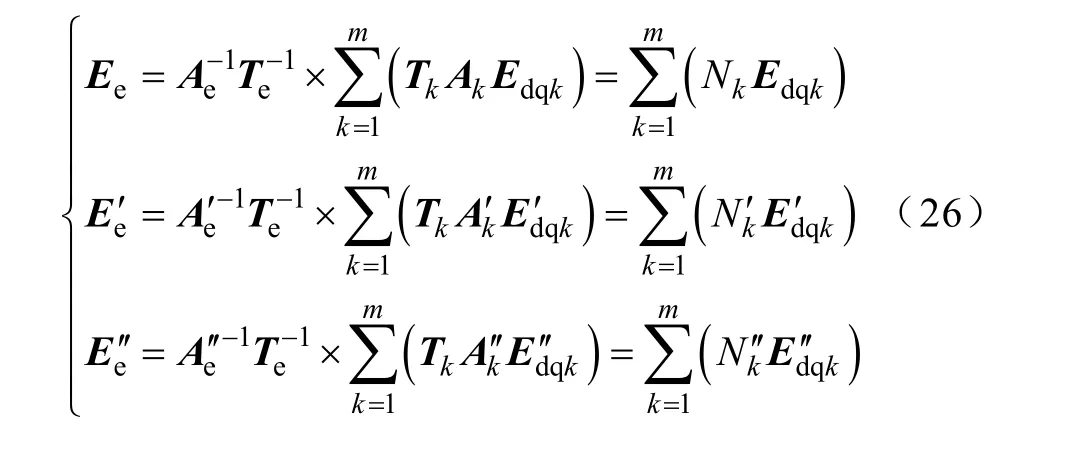
因为kN′，kN′为常数矩阵，式（26）两边微分可得

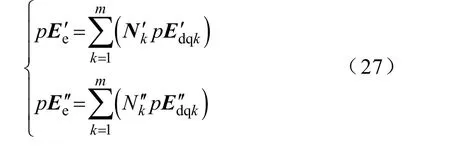
将式（27）代入式（22）和式（23）可得

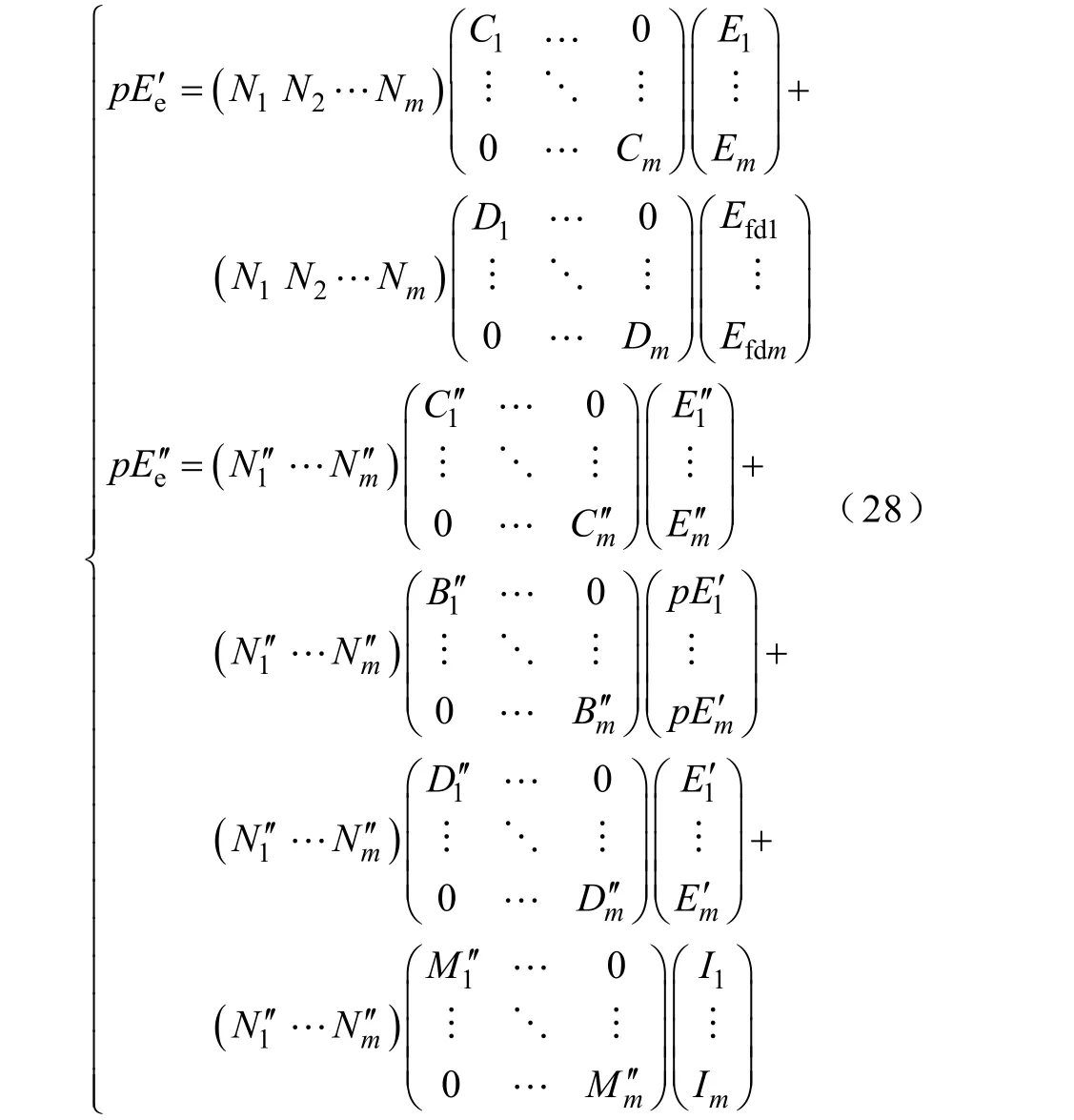
由式（26）得

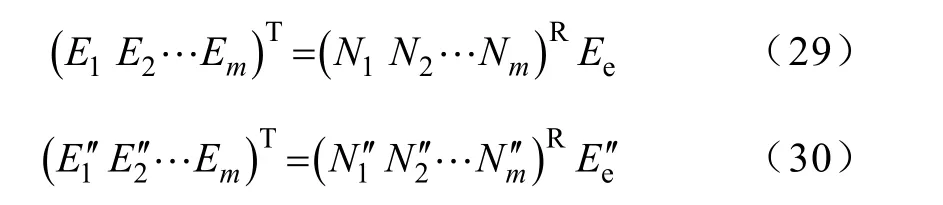
将式（29）、式（30）代入式（28）中epE′的表达式可得

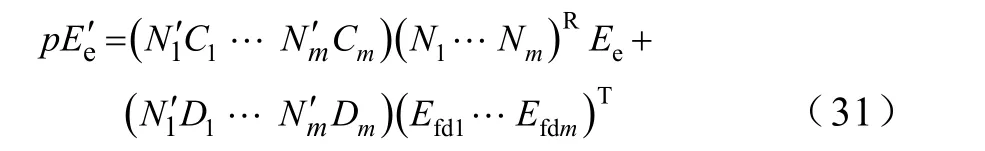
再由式（25）和式（31）可以获得等值机暂态电势微分的系数矩阵Ce，以及该微分表达式中与同调机励磁电压有关的系数矩阵e′D。

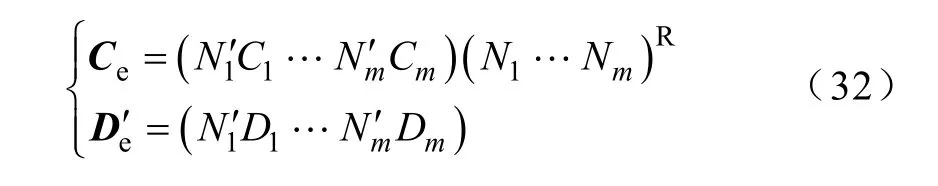
通过同样的过程，同样可以得到次暂态电势的微分表达式的系数矩阵e′′C 。

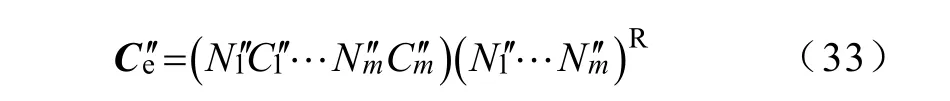
通过矩阵聚合，获得了矩阵Ce、′、 De′，被聚合的矩阵，源自同调机群中发电单元的状态模型。其 中矩阵 Ce、结构必须为一个对角阵，这样对角元素能被认为是等值开路时间常数的倒数，如式（34）所示。

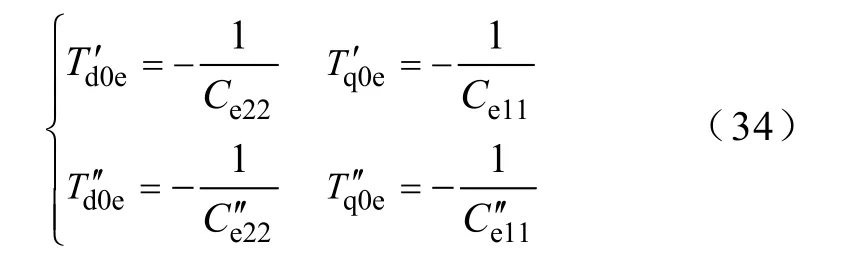
由于等值机的次暂态时间常数相当小，通过矩阵运算和使用加权获得的等值机的次暂态时间常数误差不大，对系统运行影响不大，故也可按式（35）计算。

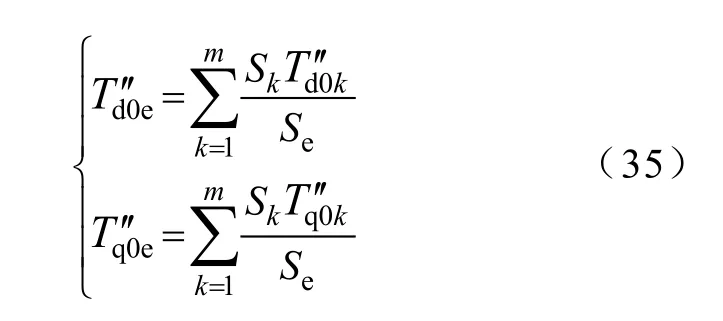
另外，应该注意的是矩阵 De′不同于式（32）所示的De，在2.3节计算加权系数时可以看出他们的区别。

2.3 励磁系统聚合

励磁系统的聚合采用了线性加权原则和模型结构保留技术的结合，所聚合的等值机励磁系统与单机励磁系统具有同样的模型结构。

励磁系统聚合时聚合步骤为：

（1）写出状态转移矩阵A、输入矩阵B、输出矩阵C。

（2）计算状态变量的加权系数。

（3）对矩阵进行线性加权计算，获得等值机励磁控制系统的转移矩阵Ae、输入矩阵Be、输出矩阵Ce。

（4）根据等值机励磁系统系数矩阵获得等值励磁控制系统的参数。

本文仿真实验在PSCAD/EMTDC环境中实现时，发电机模型使用了SCRX19励磁模型，本节将以该励磁模型为例来说明聚合方法。励磁模型的结构框图如图1所示。由结构框图可写出状态空间方程

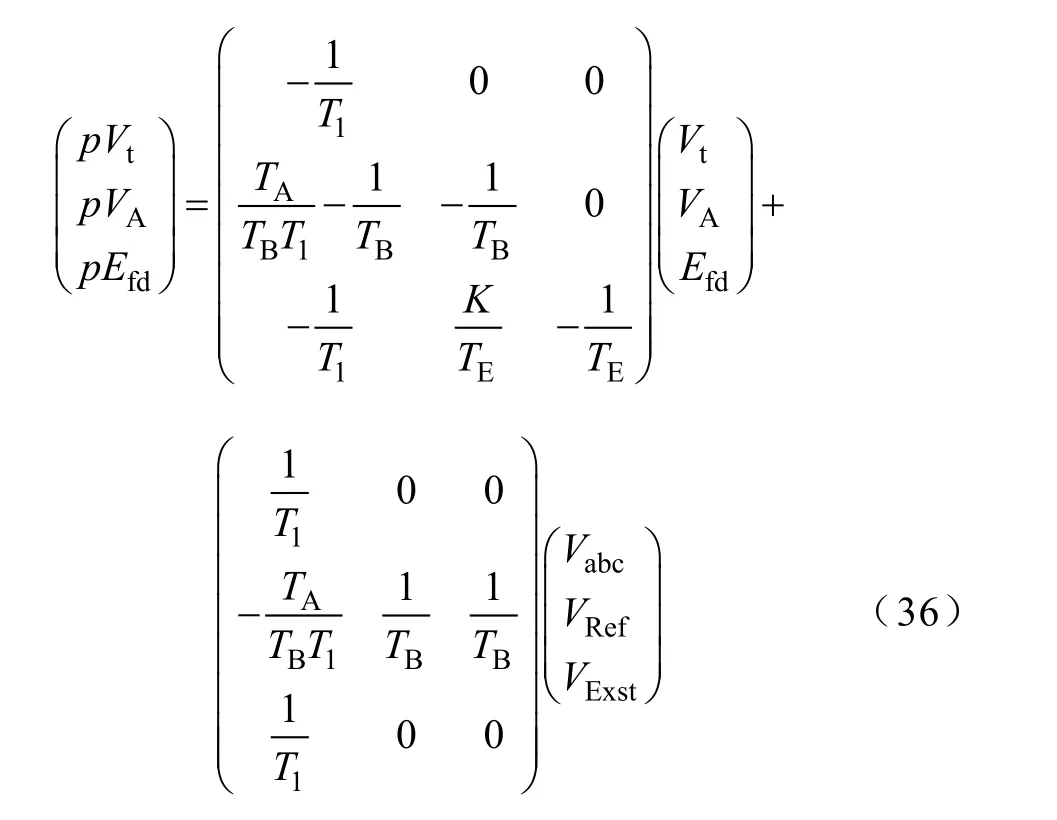
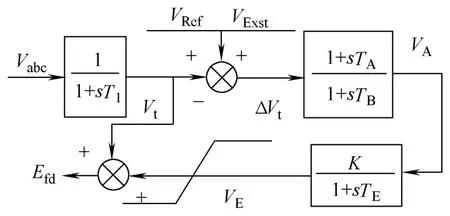
图1 SCRX19励磁模型的结构框图Fig.1 The block diagram of SCRX19 excitation model

由式（36）可知，m个同调机和等值机状态空间方程均可写为

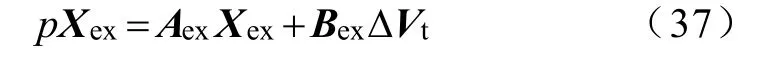
这里

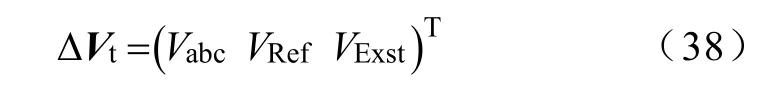
故可设加权矩阵为

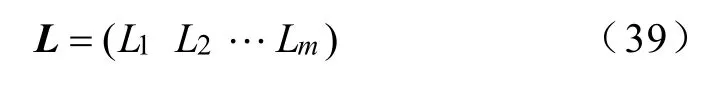
SCRX19励磁模型为三阶系统，其中

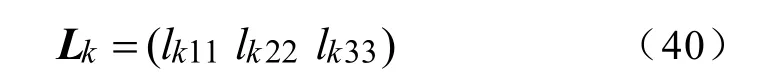
加权系数为

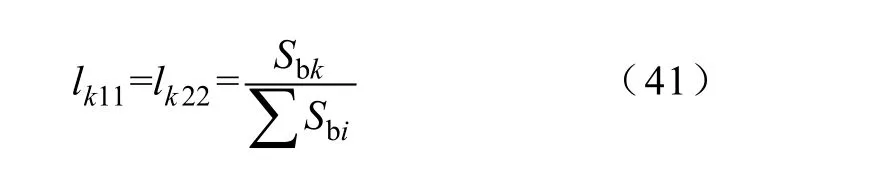
lk33和励磁电压有关，代表单机励磁电压在等值机励磁电压之间的关系。由式（21）、式（22）、式（25）进行对应项比较可得

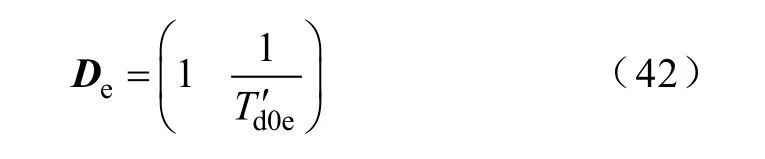
由式（25）、式（31）的第二项进行对应相等，两边左乘De的逆可得等值励磁电压关于单机励磁电压

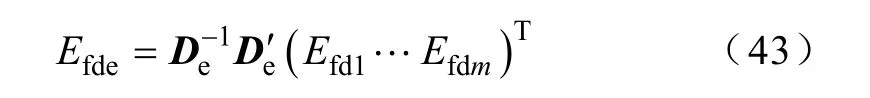
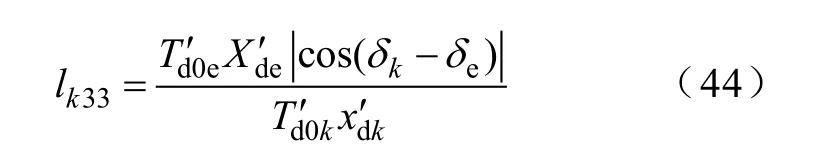
令等值机状态空间方程的矩阵为Aexe、Bexe，则由线性加权原则可得

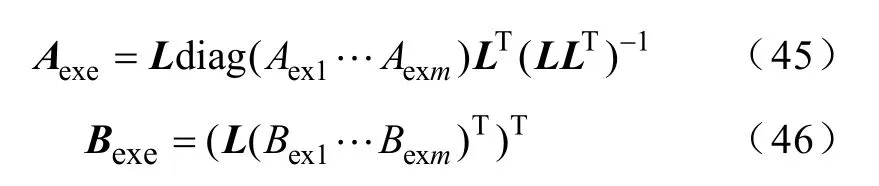
得出等值矩阵后，等值系数可以通过等值矩阵结构获得。例如： T1=- 1 /Aexe11。

2.4 调速器聚合

调速器聚合时，由于汽轮机和水轮机调速器结构不同，所以不同类型的调速器不能被聚合在一起，而要分别聚合，然后用不同的等值机表示。调速器聚合方法与励磁系统相同，加权系数的选择与励磁系统聚合时的加权系数 lk11、lk22相同，其控制系统系数，同样可以通过等值机调速器与同调机群调速器模型结构对应关系对比获得。或者在获得调速器状态空间方程的系数矩阵之后，对系数矩阵的元素采用容量加权获得等值机系数矩阵，从而获得聚合的等值机调速器。

3 系统测试

该方法被用于某舰船电力系统的动态等值，舰船电力系统在PSCAD/EMTDC中进行建模，单线图如图 2所示。励磁系统采用 PSCAD中的 SCRX19型励磁模型，调速器采用 PSCAD中的 V2 Compatible Hydro Governor（HGOV18）调速模型。

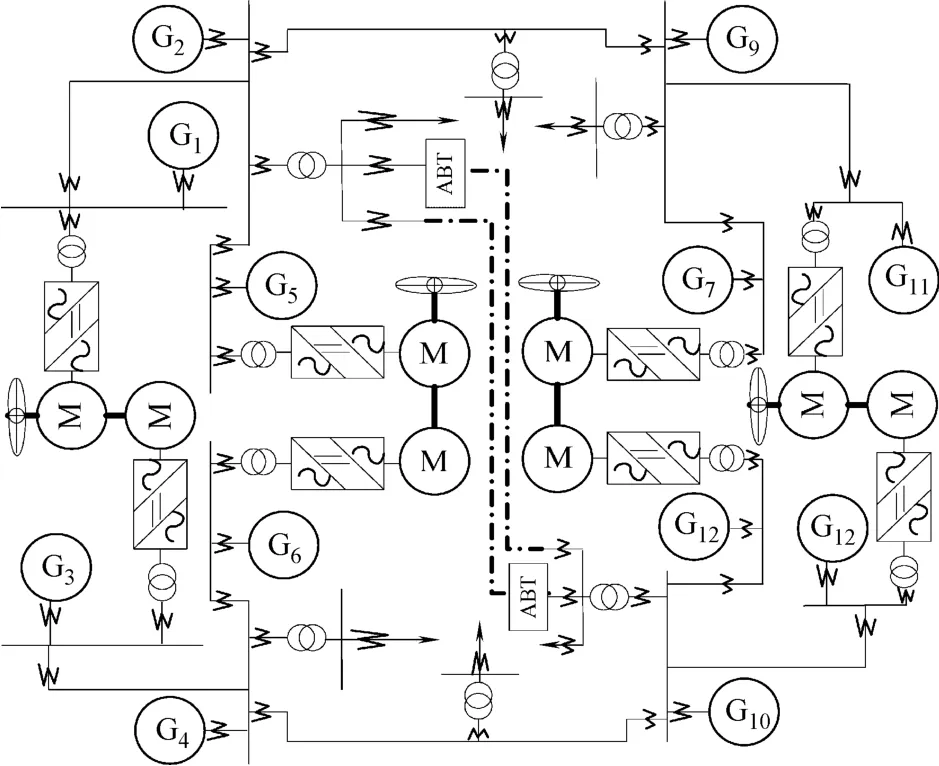
图2 某舰船电力系统单线图Fig.2 The single-line diagram of ship power system

由于 PSCAD主模型库中的发电机模型与聚合所需模型不一致，所以建模时用FORTRAN编写了适合聚合的考虑次暂态的六阶发电机模型。舰船电力系统中，经全系统仿真，可以认为发电单元7、8、9、10、11、12同调，该 6个发电单元可以被上述算法聚合为一个等值发电单元。

表1给出了应用同调聚合算法获得的等值机参数和同调发电机所用参数。表2给出了同调机和等值机励磁系统参数，表3和表4给出了同调机和等值机调速器系统参数，表中所有参数均为以各自容量为基值的标幺值。

4 仿真效果

为了验证等值效果，在如图2所示的发电机5的机端母线，在0.6s时，进行了持续0.3s的三相短路故障设置，并给出了表征等值系统和原始系统的动态性能的响应曲线。PSCAD/EMTDC中，0.5s之前，系统有一启动过程，故所有的仿真曲线均从0.5s开始，图中粗线为等值机曲线。图3给出了等值机和同调机暂态中的转子有名值角度摇摆曲线，图中可以看出，发电机基本处于同调。图4给出了等值机和同调机总机械功率对比曲线，图5给出了等值机和同调机总有功功率对比曲线，图6给出了等值机和同调机总无功变化对比曲线，图7给出了原系统和等值系统中故障母线电压变化比较曲线。由图可以看出，等值机功率总量的变化与同调机基本相同，故障母线电压变化基本相同。由等值机的仿真曲线可以看出，它可以等效6台机的变化趋势，特征曲线吻合良好，由此证明了等值效果良好。

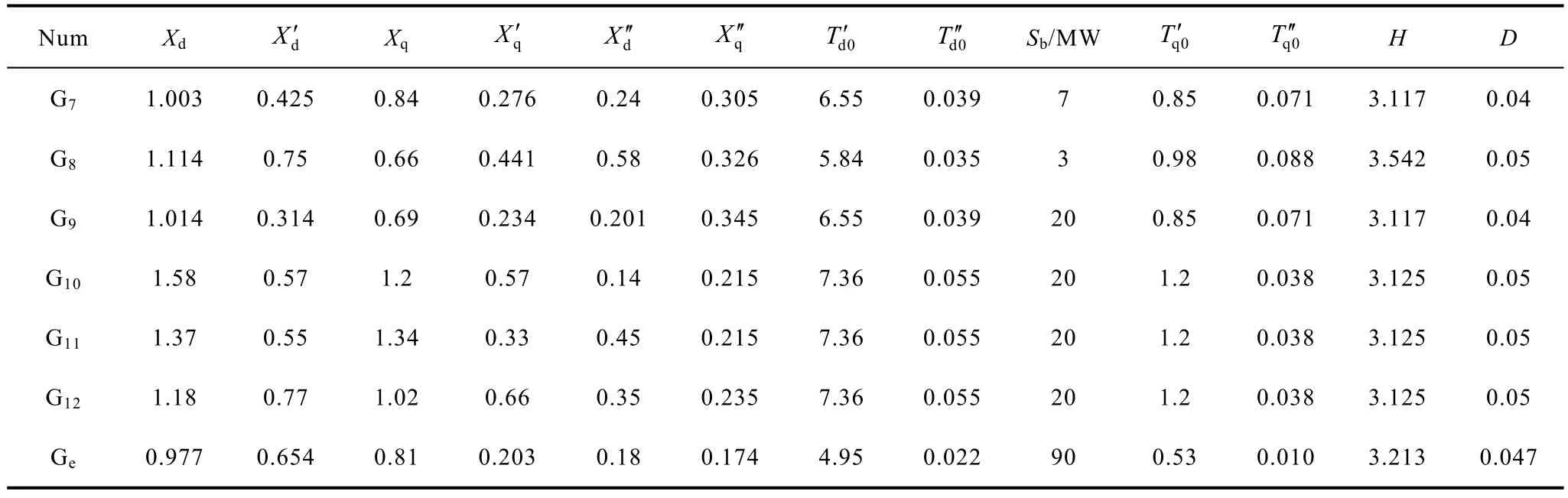
表1 同调电机和等值电机参数Tab.1 Parameters of coherent and equivalent machines

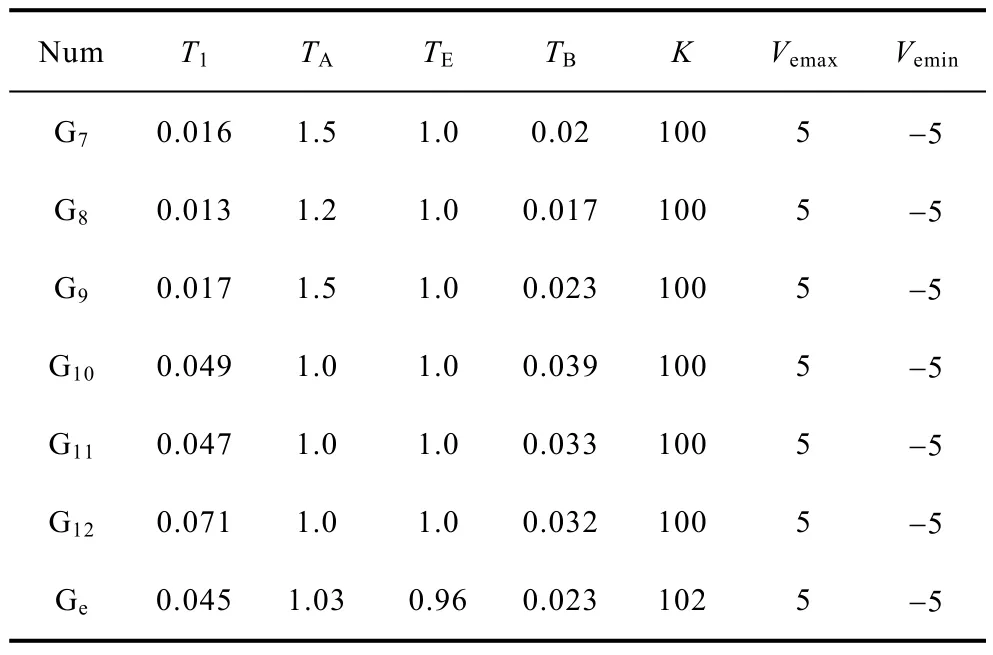
表2 励磁系统参数Tab.2 Parameters of excitation systems

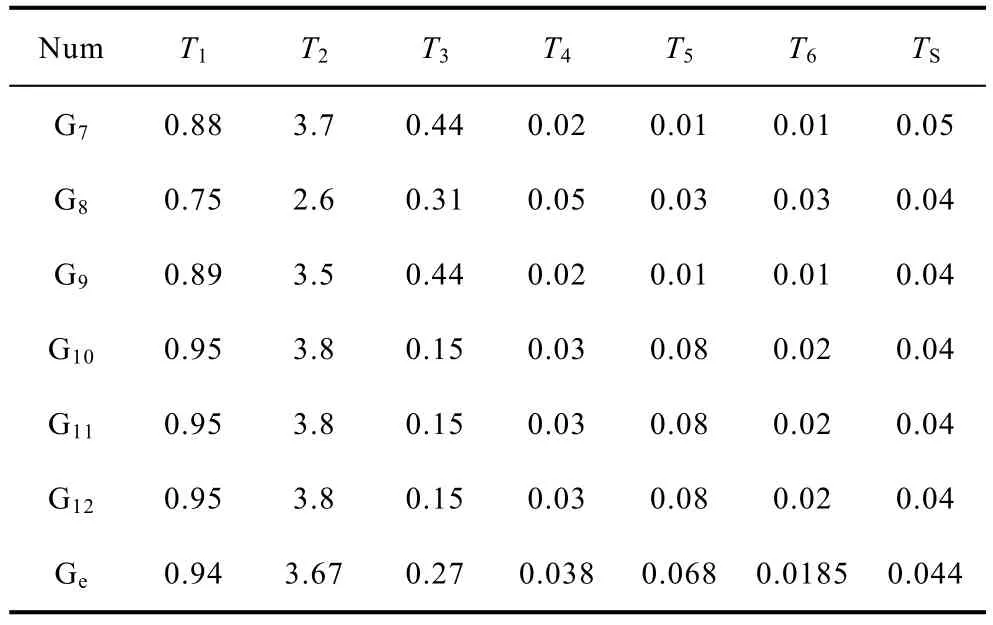
表3 调速器参数Tab.3 Parameters of governor systems

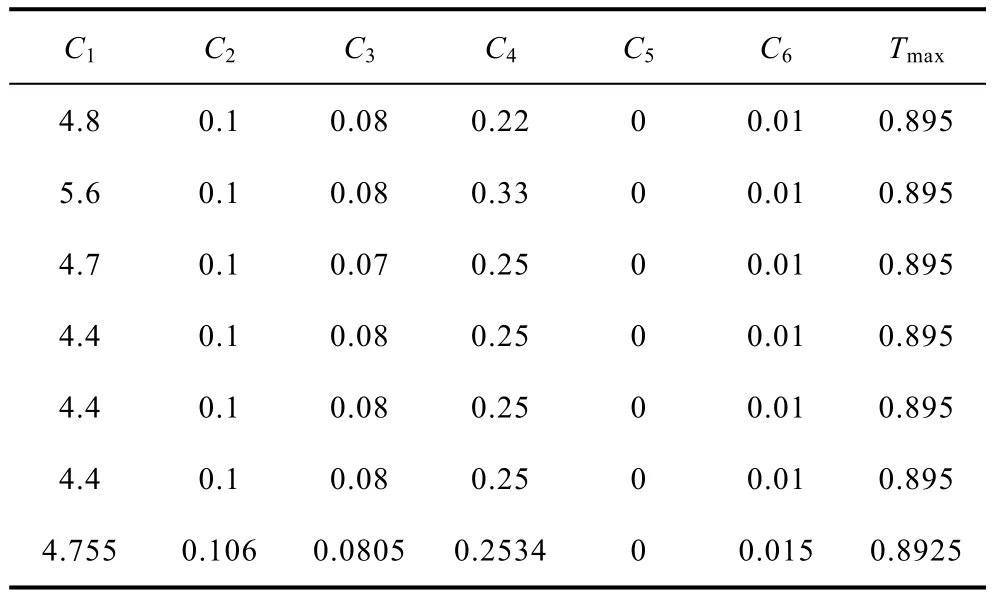
表4 调速器参数Tab.4 Parameters of governor systems

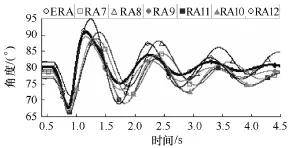
图3 同调机和等值机转子摇摆角度曲线Fig.3 The rotor swing curves of coherent machines

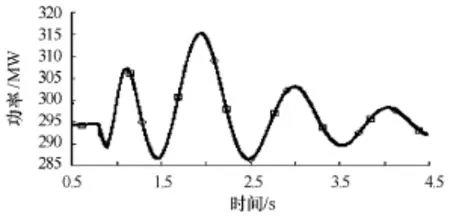
图4 同调机和等值机总机械功率对比曲线Fig.4 The total mechanical power curves of machines

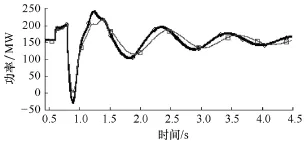
图5 同调机和等值机总有功功率对比曲线Fig.5 The total active power curves of machines

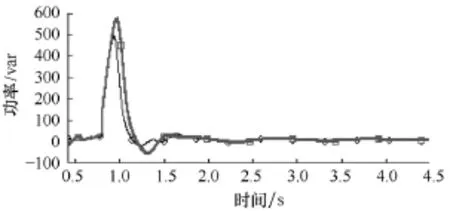
图6 同调机和等值机总无功比较曲线Fig.6 The total reactive power curves of machines

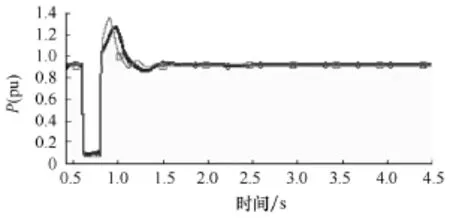
图7 故障母线等值比较曲线Fig.7 The comparison curves of fault bus voltage

5 结论

本文提出了一种同调发电机组的聚合方法，该方法基于六阶发电机模型，考虑了低阶模型忽略的实际电网中暂态和次暂态因素；时域聚合代数计算解决了频域运算的计算耗时问题；结构保留使算法可以直接应用于暂态计算程序中，减少了仿真工作量和准备时间。同时，本文给出了聚合公式及其较详细的推导过程，及可以实际应用的聚合同调机组的基本步骤。该算法在一实际舰船电力系统中的应用，表明该方法精度较好。

该方法的应用可提高在线暂态分析，在线参数计算，在线安全分析的精度和实时性，但在网络化简时，负荷模型的选用可能造成一定的误差。另外励磁系统和调速系统的状态变量聚合时，其加权系数的选择可以进一步优化。虽然推导过程是严密的数学演算，但其中进行了工程假设，我们可以通过减少工程假设，以及计及定子电磁暂态来提高该方法的精度。这些改进将是下一步研究的重点。

[1]Li Qi. AC system stability analysis and assessment for shipboard power systems[D]. Texas A&M University, 2004.

[2]Sanjeev Kumar Srivastava. Multi-agent system for predictive reconfiguration of shipboard power systems[D]. Texas A&M University, 2003.

[3]Podmore R. Identification of coherent generators for dynamic equivalents[J]. IEEE Trans. on Power App.Syst., 1978, 97(4)： 1344-1354.

[4]Ourari M L, Dessaint L A, Do V Q. Slow coherency approach for dynamic equivalents of large power systems[OL]. Session 6, paper 4. http： //www. ipst.org/IPST03papers htm#Sec6.

[5]Pei M A, Adgaonkar R P. Identification of coherent generators using weighted eigenvector[C]. IEEE Power Engng. Soc. Winter Meeting, New York/USA 1979： A79-022-5.

[6]Chow J H, Galarza R, Accari P, et al. Inertial and slow coherency aggregation algorithms for power system dynamic model reduction[J]. IEEE Trans.Power Systems, 1995, 10(2)： 680-685.

[7]Wang L, Klein M, Yirga S, et al. Dynamic reduction of large power systems for stability studies[J]. IEEE Trans. on Power Systems, 1997, 12(2)： 889-895.

[8]Germond A J, Podmore R. Dynamic aggregation of generating unit models[J]. IEEE Trans. Power App.Syst., 1978, 97(4)： 1060-1069.

[9]Ramaswamy G N, Evrard C, Verghese G C, et al.Exensions, simplifications, and tests of synchronic modal equivalencing (SME)[J]. IEEE Trans. Power Syst., 1997, 12(2)： 896-905.

[10]Galarza R J, Chow J H, Price W W, et al. Aggregation of exciter models for constructing power system dynamic equivalents[J]. IEEE Trans. Power Syst.,1998, 13(3)： 782-788.

[11]Lei X, Povh D, Ruhle O. Industrial approaches for dynamic equivalents of large power systems[C]. In Proc.Power Eng. Soc. Winter Meeting, 2002, 2： 1036-1042.

[12]Nath R, Lamba S S. Development of coherency-based time domain equivalent model using structure constraints[J]. Proc. Inst. El-ect. Eng., 1986, 133(4)：165-175.

[13]Ourari M L, Dessaint L A, Do V Q. Generating units aggregation for dynamic equivalent of large power systems[C]. In Proc. of IEEE Power Eng. Soc.General Meeting, 2004, 2： 1535-1541.

[14]Machowski J, Bialek J W, Bumby J R. Power system dynamics and stability[M]. New York：Wiley, 1997.

[15]Anderson P T M, Fouad A A. Power system control and stability[M]. 2nd ed. New York： Wiley, 2003.