基于合理低价中标的投标报价博弈分析

□文/陈偲勤

博弈论的核心思想是：假设对手在研究你的最大策略并追求自己最大利益行动的时候，你如何选择最有效的策略。投标报价是一门科学，要讲究策略和方法，报价太高，无疑会使报价失去竞争力而落标，报价太低，致使企业盈利太少。怎么实施最有利的投标报价，达到中标的目的，并且获得较高的盈利。由于投标的往往不是一个投标人，必须科学分析其他投标人报价的策略后，决定自己的投标策略，博弈论的观点可以用于投标的报价策略中。

一、博弈论与合理低价中标

（一）博弈论。博弈论可以追溯到国际象棋等的研究，而今用于政治、经济、管理科学以及军事、文化娱乐，人们的日常生活等诸多领域。博弈论，在风险不确定的情况下，研究决策主体的行为发生直接相互作用时决策以及这种决策时的均衡问题。也就是说，一个行为主体的选择受到其他行为选择主体的影响，而且反过来影响到其他主体选择时的决策问题和均衡问题。

（二）合理低价中标。投标已经成为施工企业承揽工程项目的主要方式，合理低价中标在国际工程招投标中十分流行，随着我国加入WTO和FIDIC条款的使用，建筑行业与国际接轨势在必行，合理低价中标在我国也将成为趋势。所谓合理低价，就是在成本价之上的合理低价。对工程项目进行投标报价的目的，是通过参加竞争，争取中标，通过中标获得工程项目合同的签订。实践经验证明：报价太高，无疑会使报价失去竞争力而落标；报价太低，致使企业盈利太低，甚至亏损。

二、报价的博弈分析以及模型建立

（一）投标报价的博弈类型分析

1、报价博弈的基本假设。（1）博弈规则：也就是招标人的评标方法，采用合理低价中标；（2）给定投标人i（i=1，2，3，4），其成本（ci）以及报价（bi）只有投标人自己知道，其他人不知。同时，他也不知道其他人的报价和成本。但根据自己的经验和对其他投标人的了解程度可以确定cj的定义域为［Li，Hi］上的均匀分布。其中 Li是指投标人i估计的j投标人可能的最低成本（cj），Hi是估计的可能最高成本。由于本文中要求是合理低价中标，Hi＝Bi（Bi为投标人i预测的标底价）。根据投标人i的预测，j投标人的bj=ajcj+（1-aj）Bi；其中，（1≥aj≥0）；（3）投标人的目标是尽可能中标，且使期望利润最大化。

2、投标报价的博弈模型分析。根据博弈论的定义，不难发现，招投标的整个过程其实就是投标人与投标人、招标人与招标人之间的博弈过程，他们是有着不同的利益主体，并且他们的决策之间会相互影响和作用，从而成为博弈的各方。由于各投标方不能完全了解对方的信息和决策，只能靠预测制定自己的标书，这里的标书相当于决策，并且在我国的招投标中以密封报价形式同时给出，所以投标报价属于典型的不完全信息静态博弈。

（二）投标报价的博弈模型建立。因为拍卖是规则明晰、规范化的市场，所以用博弈论来模型化拍卖是非常合适的。人们选择拍卖的动机和不完全信息博弈下的动机很相似。而低价中标下的博弈和书面密封拍卖做法类似的一种博弈模型，不同的是它属于倒置的第一价格拍卖机制。即，最低的价格就是中标；拍卖是最高出价即为“中拍”。

1、博弈模型的要素。参与人：假设n家承包单位对某项工程进行投标，那么n家承包单位就是参与人1、参与人2、……、参与人n；行动：行动是参与人在博弈的某个时点的决策变量。在此博弈模型中，博弈人的行动就是每个博弈人的报价（bi，i=1，2…n）；类型：参与人 i的类型就是他对工程项目的成本估价ci，实际的类型只有他自己知道，（ci服从［0，1］上的均匀分部）；支付：在博弈中，支付是博弈人真正关心的东西，是指在特定的战略组合下参与人得到的确定的效用水平，或者是指参与人得到的期望效用水平。

2、两个投标人的情况。首先考虑两个投标人（i=1，2）的情况，投标人的效用支付函数为：

根据纳什定理，此报价存在均衡解，也就是存在投标人效用支付最大的战略。在不完全信息静态博弈中，战略是由类型到行动的函数，即参与人i的一个战略为函数bi（ci），投标人i的出价bi（ci）是其价值ci的严格递增函数。

纳什均衡的式子为：

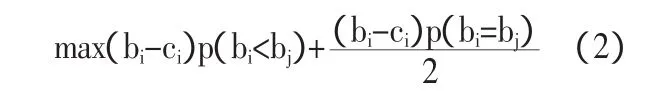
式（2）就是投标人i的期望效用最大化，p（bi＜bj）是投标人i中标的概率，p（bi=bj）/2投标人报价相同的概率。报价是连续分布，在连续分布情况下，相同出价的概率为0。因此，可以简化为：

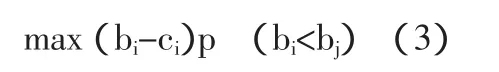
式（3）即是给定投标人i的最优反应式，所得的解就是一个纳什均衡解。

当aj≠0时，cj服从均匀分布，可得：

（7）即为我们得到的均衡结果。由于这个博弈中是两个人的决策过程，因此博弈的结果具有对称性。易知，每一个参与人最优的报价是各自的成本和估测的标底价的和的一半，并且这个报价介于成本和“标底”之间，符合合理低价中标的要求，是合情合理的。

当αj=0时，那么投标人i只要不报标底价即可；当αj=1时，虽然投标人j可以中标，但是此时他的效用为0，故此时所得的解不是均衡解。

（三）多个投标人的情况。上面是两个投标人的情况，实际中往往不会是两个投标人。

由（3）式得：投标人i中标求：

三、结论分析

（一）显见，最优报价不仅与成本价和标底价有关，还与投标人数有关。当n→∞时，最优投标价接近于成本价。也就是说，随着投标人的增加，贝叶斯均衡标价与估价之间的差异随投标人数的增加而减少。投标单位越多，投标单位获利越少。目前，我国的建筑市场竞争日益激烈，承包商的利润也逐步下降，也是一个不争的事实，原因在此也可略见一斑。

（二）随着成本的降低，引起报价的降低，中标概率将增加。承包商效用将有可能提高，不中标的效用为0，再少的盈利也比不中标好。因此，作为每个承包商，都应该把提高生产效率，降低成本作为自己提高效用的根本出发点。

（三）我们的博弈模型是不完全信息静态博弈，各个参与方所了解的对方的资料数据很少。已有的条件下，求解十分困难。投标中各个参与人的战略相同，因此各个参与人的最优策略函数也是相同的，不同的是他们的估价。由此可以得到，在这种假设下估价较高的投标人的最优报价高于估价较低的投标人。

四、结束语

合理低价中标可以使各个投标人在相对公平的条件下进行投标，遵循市场经济的原则，企业自主报价，一定程度上可以阻止投标人和中标者的不诚实交易，特别是在政府投资的项目中表现尤为突出。

在经济全球化的今天，我国的招投标制度也要和国际接轨。施工企业为了在投标中胜出，务必做到两点：对各个竞争进行尽可能准确的估计，得到尽可能多的信息；为了提高中标率以及效用，每个承包商要努力想办法降低成本。总之，博弈的真正结果，很大程度上取决于承包商个人的“能耐”和“技术”。

［1］王梦莹.使用博弈论谈价格大战[J].北方经贸，2004.8.

［2］郝丽萍.建筑工程投标报价的博弈模型研究 [J].哈尔滨建筑大学学报，2002.4.

［3］张维迎.博弈论与信息经济学[M].上海：上海人民出版社，2004.

［4］洪明等.浅析低价中标[J].施工企业管理，2002.2.