一种新的消除铁磁谐振的方法：唯一稳态消谐法及应用

冯 平, 王维俊, 王尔智

(1. 解放军后勤工程学院 机械电气工程系, 重庆, 401311；2. 沈阳工业大学 电气工程学院, 辽宁 沈阳, 110178)

一种新的消除铁磁谐振的方法：唯一稳态消谐法及应用

冯 平1,2, 王维俊1, 王尔智2

(1. 解放军后勤工程学院 机械电气工程系, 重庆, 401311；2. 沈阳工业大学 电气工程学院, 辽宁 沈阳, 110178)

提出了一种新消除谐振的方法：唯一稳态消谐法. 基本思想是如果非线性系统存在一个非谐振的正常解,并且该系统具有唯一的稳态, 则此时对应的条件就是系统不发生谐振的条件. 这一方法应用在消除中性点接地电力系统的铁磁谐振的分析中，以矩阵理论为工具，得到了相应的消谐条件. 结论表明，消除谐振的条件可以用一个常数矩阵的HURWITZ条件来决定，数值模拟验证结果正确，唯一稳态消谐法具有有效性.

电力系统；铁磁谐振；中性点接地系统；非线性系统；唯一稳态消谐法

在电力系统110～220 kV等中性点接地电力系统中，经常发生断口电容与电压互感器形成的铁磁谐振，给电力系统造成很大的危害. 围绕这种谐振的机理及消除方法，国内外进行了广泛的研究[1-2].

从方法上看，目前对这种铁磁谐振问题所采用的方法，主要有如下几个方面. 第一是实验研究[3-4].即通过大量的实验数据得到各种经验结论. 第二是进行数值模拟和仿真[5-6]. 通过建立模型，在大范围内改变参数，通过计算机计算得到或验证参数的范围. 第三是理论研究[7-8]. 即对这种谐振建立相应的数学模型，通过对模型的理论分析，了解这种谐振的机理，并且寻找消除谐振的方法. 在这3种方法中，实验和数值模拟具有直观、容易检验的优越性，但缺乏理论指导，结论有一定的局限性和猜测性；理论分析具有决定性的意义，主要有作图法[1,8]、谐波平衡法[5-6]、平面相图法[4]，幅频法、描述函数法[1-3]、非线性动态系统理论[4,7]等. 但由于该问题数学上的复杂性，目前采用的都是各种近似的方法，得到的结论和试验数据往往有一定的差距. 因此，提出和发展新的分析铁磁谐振的方法，对该问题进行更深入的分析是很有意义的.

消除非线性系统的谐振在许多领域都具有理论和工程的意义. 本文提出了一种新的消除非线性系统谐振的方法：唯一稳态消谐法. 该方法的基本思想是如果非线性系统存在一个非谐振的正常解, 并且该系统具有唯一的稳态, 则此时对应的条件就是系统不发生谐振的条件. 本文将这一方法应用在消除中性点接地电力系统铁磁谐振的分析中，以矩阵理论为工具，得到了相应的消谐条件. 本文的结果表明，消除谐振的条件可以用一个常数矩阵的HURWITZ条件来决定，并用数值模拟进行验证，表明结果正确，同时也说明了唯一稳态消谐法的有效性.

1 唯一稳态消谐法的基本定理

设其中一个解是系统的非混沌谐振的常态解，如若式(5)的零解是全局渐近稳定的，即

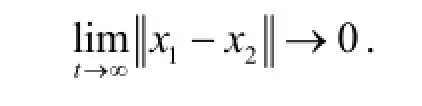
则该系统的稳态解唯一，即系统(1)没有谐振.

对定理1做如下几点说明：

a. 实际上系统中的常态解x1往往可以通过大量的运行和观测得到.

b. 由定理1知道，消除谐振的问题，就转化为寻求系统稳态解唯一问题.

c. 定理1的应用要解决3个问题，一是将非线性系统(1)化为线性时变系统(5)的形式，二是常态解的存在性的寻找，三是系统唯一稳态的判定.

下面以电力系统铁磁谐振消谐条件为例来讨论.

2 定理条件的讨论

2.1 非线性电路化为线性时变电路

考虑非线性电路N，其描述方程为非线性方程：

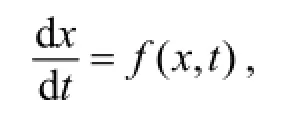
各量满足式(1)的条件.

电路中的元件满足以下关系：

a. NL时变非线性电感

由此，完成了将非线性电路系统(1)化为时变线性系统(9).

2.2 常态解的寻找

对于电力系统铁磁谐振，大量实验和运行经验表明其有多个稳态解，其中最常见的稳态解，就是没有发生谐振时，对应于系统正常工作状态的稳态解. 系统的其他非正常的稳态解，则是由于扰动，引起C与L之间的铁磁谐振造成的稳态解. 显然这些非正常的稳态解对于系统是有害的，如果我们能够使经扰动后的非正常稳态解趋于正常的稳态解，即使系统的稳态解唯一，那就可以达到消除系统铁磁谐振的目的，因此，对于电力系统铁磁谐振来说，这个问题可以用正常解来代替[9].

2.3 系统唯一稳态的判定

非线性电路系统的唯一稳态问题是一个非常重要，而又很困难的问题. 国际电工委员会电路与系统分会主席，著名非线性电路理论专家L.O.Chua教授对这一问题有非常广泛和深入的论述，并在其经典著作中概述了目前已有的结果[10]. 但目前已有的经典结果，与实际观察的参数范围，有较大的差距. 所以，改进已有的结果，在理论与实用两个方面，都有重要的意义.

因此，电路的唯一稳态的问题，就化为(9)的零解全局渐进稳定的问题，对于这个问题，有很多解决方法，例如，对于式(9)，有如下的定理2[4]：

3 消除铁磁谐振条件分析

下面以消除电力系统铁磁谐振条件为例，说明唯一稳态消谐法的应用.

考虑如下铁磁谐振电路[3]：

图1 铁磁谐振等效电路

由定理2，式(10)其对应的M矩阵，得到图1所示的铁磁谐振电路不发生谐振的条件为定理3.

定理3 图1所示电路，其不发生谐振的条件为：

上述参数满足定理3，该电路有唯一稳态，无谐振发生. 用计算机模拟，与结论相符.

4 结论

本文提出了一种新的消除谐振的方法：唯一稳态消谐法，并以铁磁谐振电路为例进行了验证，说明本文提出的方法是有效的.

[1] 解广润. 电力系统过电压[M]. 北京： 水利电力出版社, 1985.

[2] 张纬钹, 高玉明. 电力系统过电压与绝缘配合[M]. 北京： 清华大学出版社, 1988.

[3] 郑盛琼, 陈维贤, 鲁铁成. 110-220 kV变电所中互感器引起的铁磁谐振及吸能消谐[J]. 高压电器, 1996, 18(6)：26-30.

[4] Henriksen T. How to avoid unstable time domain responses caused by transformer models[J]. IFEE Trans on Power Delivery, 2002, 17(2)： 516-522.

[5] 李兴斌, 王晨新. 断路器均压电容引起的铁磁谐振分析[J]. 东北电力技术, 1994, 24(9)： 39-43.

[6] 贾红琴. 电磁式PT所致铁磁谐振过电压分析及抑制[J].高电压术, 2000, 43(1)： 69-70.

[7] 石峰. 110-220 kV变电站空母线铁磁谐振的分析[J].湖南电力, 2001, 15(1)： 14-16.

[8] Yunge Li, Wei Shi. A Systematical Method for Suppressing Ferroresonance at Neutral-Grounded Substations[J]. IEEE Transactions on Power Delivery, 2003. 18(3)：1009-1014.

[9] 冯平, 王尔智. 中性点接地电力系统三相铁磁谐振理论分析[J]. 电工技术学报, 2004, 23(4)： 35-39.

[10] Chua L O. nonlinear Circuit： An Overview of Ten

Years[J]. Systems and Computers, 1994, 4(2)： 117-159.

A new method to eliminate ferroresonance: unique state elimination method

FENG Ping1,2, WANG Wei-jun1, WANG Er-zhi2
(1. Department of Mechanical and Electrical Engineering, Logistical Engineering University, Chongqing 401311, China; 2. Faculty of Electrical Engineering, Shenyang University of Technology, Shenyang 110178, China)

A new method for eliminating resonance in nonlinear system, unique steady state elimination method is presented. Its basic idea was that if there is a normal (non-resonance) solution for the system, and the steady state of system was unique, then the corresponding conditions were the conditions for eliminating esonance. This new method is applied to analyze the eliminating of ferroresonance in neutral grounding power system. Based upon metrix theory, the conditions for eliminating this ferroresonance are obtained ,which can be determined by the Hurwitz conditions of some constant matrixes. The conclusions of this article are proven correct by numerical simulation, and it shows the effectiveness of unique steady state elimination method.

power system; ferroresonance; neutral grounding power system; nonlinear system; unique steady state elimination method

TM 13

符：A

1672-6146(2010)04-0045-04

10.3969/j.issn.1672-6146.2010.04.013

2010-09-20

国家自然科学基金资助项目(50477050)

冯平(1961-), 男, 博士, 副教授, 从事电路理论及高压电器理论研究.