不定方程x2+y4=zn的一类非本原解

管训贵

(泰州师范高等专科学校 数理系, 江苏 泰州, 225300)

不定方程x2+y4=zn的一类非本原解

管训贵

(泰州师范高等专科学校 数理系, 江苏 泰州, 225300)

运用初等方法证明了对于任何正奇数n，不定方程24nxyz+=都有无穷多组正整数解(,,)x y z，并且给出了该方程的一类非本原解(,,)x y z.

不定方程；正奇数；非本原解

1 引言及主要结论

2004年，M. A. Bennett和C. M. Skinner[1]证明了：当n为大于4的偶数时，方程(2)无本原解(x,y,z).同年，J. S. Ellenberg[2]证明了：当n有适合p≥211的奇素因数p时，方程(2)无本原解(x,y,z). 这2个结果的证明都要用到极其高深的数学理论. 不难发现，方程(2)是否有本原解，还需要考虑适合5≤ p ≤199的奇素数p. 尽管只剩下有限的几种情形，但讨论起来却十分困难.

2009年，乐茂华[3]用初等方法证明了：5n=时，方程(2)无本原解(,,)x y z，但证明过程相当复杂，此外，还运用了一些特殊的技巧. 看来要想解决其它情形，必须另辟蹊径[4].

本文不涉及方程(2)的本原解，而给出n为正奇数时方程(2)的一类非本原解.

定理1 设m为非负整数，则方程：

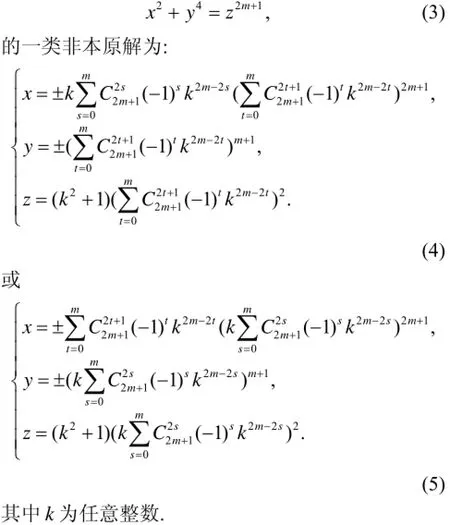
2 关键性引理

3 定理的证明

令akb=(k为任意整数)，则由引理1知：

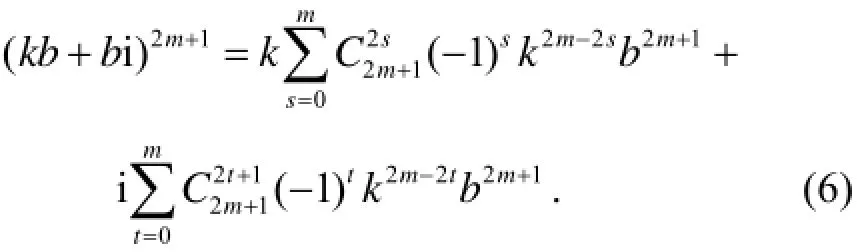
对式(6)两边取复数模得：

由式(9)知，式(3)的一类非本原解为式(5).

定理得证.

[1] Bennett M A, Skinner C M. Temary Diophantine equation va Galois representations and modular forms[J]. Canada J Math, 2004, 56(1)： 23-54.

[2] Ellenberg J S. Galois representations attached to Q-curves and the Generalized Fermat equation A4+B2=Cp[J]. Amer J Math, 2004, 126(4)： 763-787.

[3] 乐茂华. 关于Diophantire方程x2+y4=z5[J]. 云南师范大学学报： 自然科学版, 2009, 29(4)： 1-5.

[4] 乐茂华. 具有连续尾数的本原Pythagoras数组[J]. 湖南文理学院学报： 自然科学版, 2007, 19(2)： 2.

A class of non-primitive solutions of the Diophantine Equation24nxyz+=

GUAN Xun-gui
(Mathematics ＆ Physics of Taizhou Normal College, Taizhou 225300, China)

By some elementary methods, it was proven that, for any positive odd integer n, the Diophantine equation x2+y4=znhad infinitely many positive integer solutions (x, y, z). Moreover, a class of non-primitive solutions (x, y, z) of the equation were given.

diophantine equation; positive odd integer; non-primitive solution

O 156

：A

1672-6146(2010)04-0017-02

10.3969/j.issn.1672-6146.2010.04.006

2010-08-19

泰州师范高等专科学校重点课题资助项目(2009-ASL-04)

管训贵(1963-), 男, 副教授, 主要研究方向为基础数论.