火炮全弹道过程仿真及应用
李克婧,张小兵
(南京理工大学动力工程学院,江苏 210094)
目前,现有的文献资料多是针对某一具体弹道段内的过程(如内弹道过程、外弹道过程和气动力过程等)进行讨论研究[1-3],忽略了它们之间的相互作用和影响。而火炮系统是由弹、药和炮3个子系统共同组成的,从宏观上看其发射过程是由3个子系统共同作用的结果[4],从微观上看整个弹道过程是由诸多参量相互作用而成的复杂过程,每个弹道段之间紧密联系,其中任一参量的变化都有可能给整个武器系统带来很大影响[5],显然,仅单独研究某一弹道段是不可能真实反映出火炮系统的弹道过程的。因此十分有必要建立一套完整的全弹道过程仿真软件,以便对全弹道过程的系统研究。
1 全弹道仿真模型建立
1.1 内弹道模型
本文选择了当前应用范围较广的以热力学为基础的经典内弹道理论和以两相流体力学为基础的现代内弹道理论这两种模型。
1)经典模型是一种建立在拉格朗日假定下的空间平均参数模型。经典模型,对于膛压不太高的火炮,理论计算与实验结果具有较好的一致性。式(1)是基于经典内弹道理论的数学模型。对于主装药为多孔火药的,i表示发射药种类;ψi方程应改写为以下计及分裂点的形状函数,即:
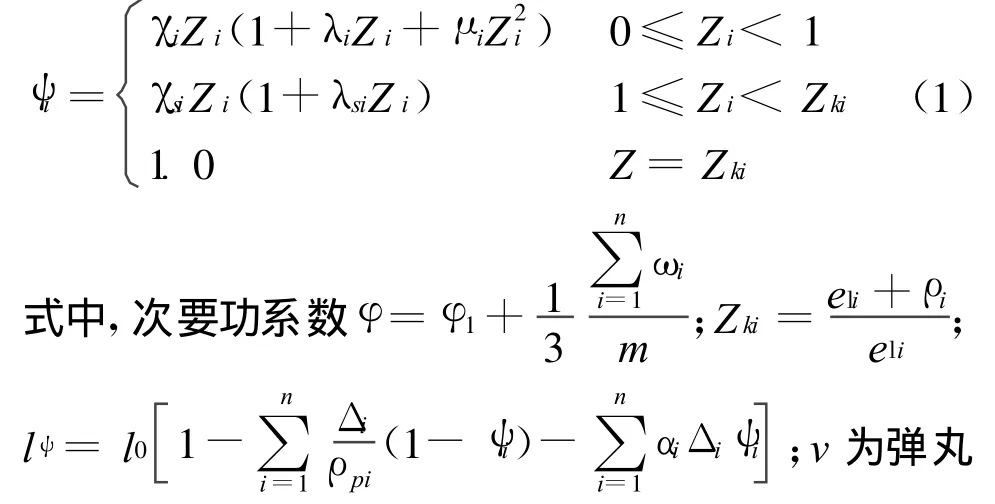
速度;p为火炮膛内平均压力;l为弹丸行程;lψ为自由缩颈长。这里的ψi火药形状函数随不同的装药结构以及火药形状改变,从仿真软件的通用性考虑,这里给出的是n种火药的混合装药结构,具体采用何种装填方式及火药类型要根据实际需要进行选择。对于方程组采用四阶精度的龙格-库塔法来求解。
2)两相流内弹道模型,对大装填密度、高膛压火炮装药安全设计具有十分重要的意义。式(2)是采用底部点火方式的两相流内弹道数学模型,这里只列出了核心的基本方程组,具体应用还需要根据装药结构、点传火方式、火药种类等不同,对方程进行相应变换,其他辅助方程及定解条件可参见相关文献[6]。

式中:˙mc为火药燃烧生成气体源项;˙mign为各种点火具的源项;φ为空隙率;A为药室横截面积;ρg、ρp分别为气相、固相密度;ug、up分别为气相、固相速度;QP为相间传热;fs为相间阻力,对基本方程使用具有二阶精度的MacCormack差分格式[7]进行计算。
1.2 后效期效应
弹丸出炮口后,膛口的气体向外喷射是一个非常复杂的过程,高速、高压的火药气体是属于非定常完全膨胀射流,应用一般的紊流射流理论很难解决膛口气体的流场问题,对于不同的弹药处理方式也不尽相同,为使软件通用性更强,这里仅讨论火药后效期的作用,依据经验公式在这里将实际炮口速度v0与内弹道结束的计算结果v g[4]简化处理为v0=v g(1+2.5%)。
1.3 气动力计算与外弹道模型
弹丸外形对气动力的影响很大,本文以工程计算方法为基础结合风洞试验,对弹丸进行气动力计算。由弹丸的外形参数、攻角、Ma就可计算出弹丸以不同Ma和攻角在空中飞行的气动系数,包括阻力系数、升力系数、压心系数、俯仰力矩系数及其导数、俯仰阻尼力矩系数及其导数、滚动力矩系数及其导数、滚动阻尼力矩系数及其导数等[3]。外弹道的计算与气动力计算相结合,解算出弹丸在空中飞行时不同位置的弹道诸元,包括弹丸的速度,弹道倾角,飞行高度,飞行距离和时间等诸参量。
1)用于计算外弹道的数学模型种类繁多,一般依据弹药种类及计算需要来建立,六自由度刚体模型是最基本的计算模型[8],该模型包含12个弹道变量,可以详细描述弹丸在空中的飞行姿态及各弹道参量的变化过程。
2)为了简化计算和实际需要,常常在六自由度刚体模型的基础上进行相应简化及变型,简化模型种类繁多,本文只列出以飞行斜距离为自变量的质点弹道模型:
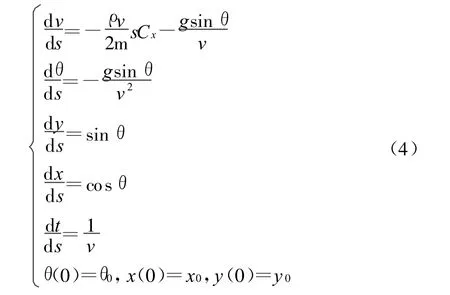
式中:m为弹丸重量;Cx为阻力系数;ρ为空气密度;g为重力加速度;θ为弹道倾角。
1.4 终点毁伤模型
穿甲弹主要是对目标的侵彻作用。对于穿甲弹的威力一般用弹道极限v b来衡量,它在终点弹道学中是指对装甲有效的撞击速度,本文的穿甲弹属于长杆式次口径穿甲弹,因此采用以下公式[9]:

式中:dc为弹杆直径;mc为飞行弹丸质量;λ取为0.85;K为穿甲系数取2 300;b为靶板厚度。
本文采用以下穿甲模型,美国 Tate等人提出的垂直穿深公式:

式中:d为弹径;L u为有效穿甲长;p为垂直穿深;px为垂直侵彻半无限厚板的深度;Δs为有限厚板背向效应引起的侵彻增量;vc为着靶速度;vk1为零侵彻所对应的最大速度(一般取850m◦s-1)。
2 仿真软件设计
全弹道过程仿真软件采用适合工程计算的Visual Basic语言编码,同时,它具有界面可操作性强的优势,采用分块开发的形式,各模块基本上能独立完成某单一的任务,每个模块为一个子程序段,程序段之间通过虚实元结合以及定义变量名称公用区的方式进行数据传递。在程序运行的每个阶段可随时开始、暂停或终止仿真程序的运行以及进行仿真参数的修改等,便于调试开发。
仿真软件的7个模块分别是前处理模块、装填参量模块、内弹道计算模块、气动力计算模块、外弹道计算模块、终点毁伤模块和后处理模块。
2.1 系统仿真流程图
系统流程图如图1所示。可以看出,该程序设计具有灵活的操作性。
2.2 仿真系统软件功能实现
2.2.1 输入模块及初始参数设定
根据攻击目标的特性用户可任意选择火炮系统所提供的装药结构方式以及弹道计算方式,确认选择后进入初始参数输入界面,弹道根据选择的弹药外形特点将其对应的弹道参数进行修改,软件还给出提示对话框以避免因中途输入数据出错而导致程序中断。
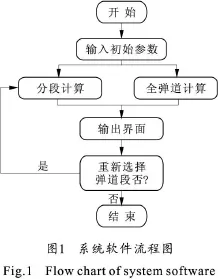
2.2.2 分段计算模块
在用户选择了分段计算方式后进入该界面后,需要选择对应弹道段的计算方式。在分段计算中设置复选框功能,用户可选择其中一个或多个选项,且无顺序要求。软件的内弹道模块中包含了1.1节所介绍的两种模型。外弹道计算也有质点弹道模型和六自由度模型供用户选择,这里给出的是单选框设置。
2.2.3 全弹道计算模块
若用户选择的是“全弹道计算”方式,此模块是将各个弹道段联系起来直接进行计算并得到最终结果。
2.2.4 显示模块
如果用户选择的是“分段计算”,则在显示窗口只可查看对应弹道段上的主要参数结果,同时可以按“重新选择弹道段”返回选择弹道段界面来重新选择需要的弹道段再查看其结果。如果选择“全弹道计算”,则可以查看每个弹道段的主要参量值,此时“重新选择弹道段”这个选择按钮为灰化状态。
3 实例应用与分析
为了证明该软件正确有效,利用下面算例进行验证计算:尾翼稳定脱壳穿甲弹,9/7单一粒状药,底部点火方式,采用全弹道计算方式,其中内弹道采用一维两相流内弹道模型进行计算,外弹道计算选择6自由度刚体弹道模型,毁伤威力以比动能的形式给出,通过全弹道仿真软件的计算得到的仿真结果以格式文件和图形方式给出。算例中具有代表性的部分参量曲线如图2所示。
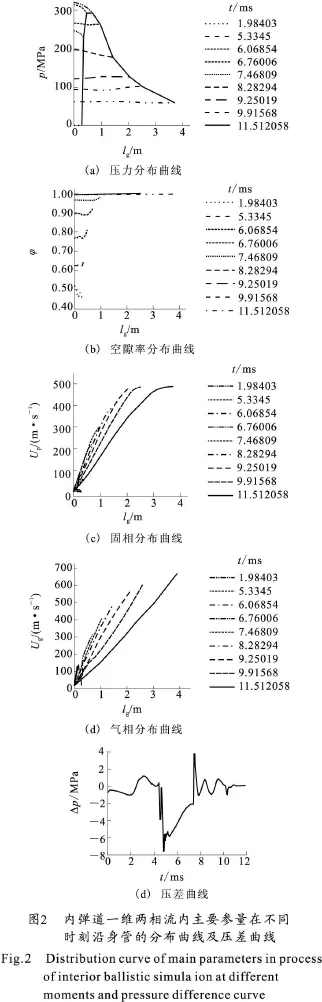
利用一维两相流数值仿真方法可以直观地刻画火药颗粒、燃气、弹丸、压力等主要参量随时间和空间的变化曲线,此外压力波是保证火炮装药安全射击的关键也是研究者关注的主要参量之一,因此,在图2中列出了弹丸速度v、压力 p、压差Δp随时间的变化曲线,以及压力p、空隙率φ、火药颗粒速度up及气相速度u g在不同时刻沿火炮身管的分布曲线。
利用空隙率 φ的变化曲线来解释膛内的物理现象:火药颗粒全面点火前t<5.334 5 m s,由于气固两相间的相间阻力及固体颗粒间的颗粒应力作用,推动固体颗粒向弹底方向运动,从而使靠近膛底附近的固体颗粒越来越稀疏,空隙率逐渐增大,靠近弹底附近的固体颗粒越来越密集,空隙率逐渐下降,曲线中间有一段波动较大,原因是该炮的坡膛部分截面积变化较大导致的;由于火药燃烧不断生成气体,整个膛内空隙率均逐渐上升,由于弹后纯气相区的存在,使弹底附近的空隙率接近于1,当t>11.512 08m s时,膛内空隙率均大于 0.99,火药几乎全部燃烧完毕,内弹道过程完成,其中压力波Δp<8 MPa在火炮设计安全范围内。曲线的变化趋势符合火炮膛内实际的基本物理现象[9]。
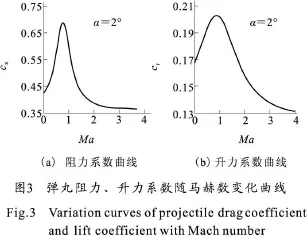
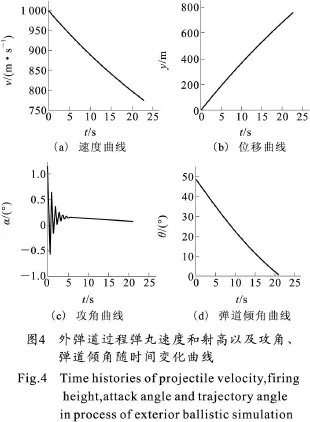
在弹丸飞出炮口以后,产生后效期作用,一方面是对火炮身管的后效作用,另一方面是对弹丸的后效作用,在膛口气流的推动下,使弹丸初速由v g增加到v0,然后弹丸开始在空中的运动即外弹道过程,利用气动力计算得到弹丸在空中飞行过程所受到各种力和力矩的作用,再结合6自由度刚体数学模型来描述弹丸在飞行过程中的各种姿态和弹道参量的变化。图3是阻力系数Cx和升力系数Cy随Ma的变化曲线,攻角 α=2°时,当M a<1.2时阻力系数和升力系数随M a增加而增加,且Cx的变化比较剧烈而Cy的变化较平缓,当Ma>1.2时阻力系数和升力系数随Ma的增加而降低,当Ma>3后阻力系数和升力系数的变化均趋于平缓,符合气动力规律,气动力参数变化趋势与风洞试验也有较好的符合[3]。图4列举了弹丸速度v和弹丸射高y随飞行时间的变化曲线,以及攻角α、弹道倾角θ随时间的变化趋势,鉴于篇幅限制在此并未列出所有参量的变化曲线。弹丸从出炮口的v0=984 m◦s-1(已考虑后效期的影响)直到飞达毁伤目标,由于阻力作用弹丸速度不断降低,与等效靶板作用后得到弹道极限vb=108.8 m◦s-1,侵深为Δs=86.9 mm,完成全弹道过程。
4 结 论
1)通过对武器全弹道过程的描述,利用VB语言创建完整的弹道过程仿真平台。
2)建立了各弹道段上不同的数学模型,方便实际应用需要,仿真软件兼具全弹道计算和分段计算的功能,此外,采用模块化设计有利于拓展软件功能,开发通用武器系统仿真软件。
3)通过对脱壳穿甲弹的全弹道过程仿真得到数据文件,可以较好地解释弹道过程中的各种物理现象,为武器全弹道系统研究提供了强有力的工具。
[1] 杨艳明,唐胜景.基于Simulink的子导弹全弹道仿真[J].系统仿真学报,2006,18(6):1442-1449.YANG Yan-m ing,TANG Sheng-jing.T rajectory simu lation of submunitions based on simu link[J].Journal o f System Simu lation,2006,18(6):1442-1449.(in Chinese)
[2] 汤瑞峰,易文俊.大口径尾翼稳定脱壳穿甲弹全弹道优化设计[J].兵工学报,1997,18(3):208-211.TANG Rui-feng,Y IWeng-jun.Optimization design o f large calibre fin stab lited sabot discarded penetrator[J].Acta A rmamentarii.1997.(in Chinese)
[3] 周长省,鞠玉涛.火箭弹设计理论[M].北京:北京工业大学出版社,2005:165-176.ZHOU Chang-sheng,JU Yu-tao,Rocket projectile design theory[M].Beijing:Beijing Technology University Press,2005:(165-176)(in Chinese)
[4] 王绍明.弹道系统软件的需求分析及模块结构图[D].南京:南京理工大学,1993:31-41.WANG Shao-m ing.Needs analysis and module structure diagram of ballistic system software[D].Nanjing:Nanjing University of Science and Technology,1993:21-41.(in Chinese)
[5] 王涛.高炮弹道仿真研究[J].系统仿真学报,2004,16(6):1184-1186.WANG Tao.Study on ba llistic trajectory simulation in antiaircraftartillery[J].Acta Simulata Systematica Sinica,2004,16(6):1184-1186.
[6] 袁亚雄,张小兵.高温高压多相流体动力学[M].哈尔滨:哈尔滨工业出版社,2005:182-194.YUAN Ya-xiong,ZHANG Xiao-bing.H igh tem perature high pressuremultiphase flow dynamics[M].Harbin:Harbin Industry of Technology Press,2005:182-194.(in Chinese)
[7] 申越,袁亚雄,张小兵.超高射频武器系统的内弹道一维两相流数值仿真[J].兵工学报,2005,26(5):600-60.SHEN Yue,YUAN Ya-xiong,ZHANG Xiao-bing.One-dimension two-phase flow numerical simulation of interior ballistics for hyper firing-rate weapon system[J].Acta Armamentarii,2005,26(5):600-60.(in Chinese)
[8] 徐明友.火箭外弹道学[M].哈尔滨:哈尔滨工业出版社,2004.XU M ing-you.Rocketexterior ballistics[M].Harbin:Harbin Industry of Technology Press[M].2004.(in Chinese)
[9] 隋树元,王树山.终点效应学[M].北京:国防工业出版社,2000.SUIShu-yuan,WANG Shu-shan,Term inal effect[M].beijing:Nationy Defence Industrial Press,2000.(in Chinese)

