坦克全电式炮控系统自适应摩擦补偿控制研究

朱志昆,李长兵,李年裕,张 健

(装甲兵工程学院控制工程系,北京 100072)

坦克全电式炮控系统是指水平和垂直分系统都采用电机通过机械传动装置驱动火炮。与电-液式、全液式炮控系统相比较,全电式炮控系统部件减少、结构更简单;系统工作时噪音低、效率高;不存在“二次效应”的危害。坦克火炮主要进行点-点的射击,火炮的定位精度以密位计,火炮的低速瞄准特性作为系统的一个重要指标,将直接标示着坦克炮控系统的整体性能。对于全电式炮控系统而言,传动装置的非线性摩擦力矩是影响系统低速性能的主要因素之一。自适应控制通过计算炮控系统模型参数的变化,能克服由于非线性摩擦和对象模型参数的不确定性对系统造成的影响。

1 系统摩擦力矩特性分析

摩擦力矩广泛存在于机械传动机构中,摩擦模型的研究经历了较长的时间,传统的摩擦模型是摩擦力正比于负载,与运动方向相反。目前工程上研究和应用最多的是Stribeck摩擦模型,摩擦力矩T f可以表示为[1]:

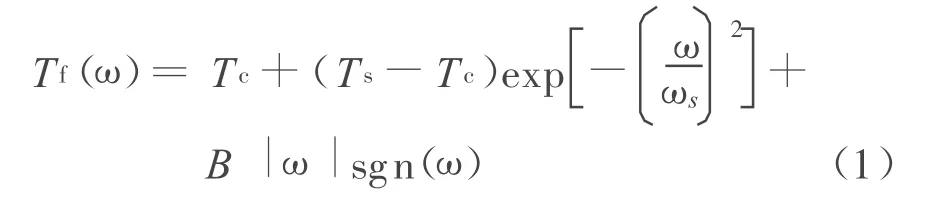
式中:ω为物体相对运动速度;ωs为Stribeck摩擦模型中的临界速度;T c为库仑摩擦力幅值;T s为最大静摩擦幅值;B为粘滞摩擦系数;sgn()为符号函数。Stribeck摩擦模型的结构如图1所示。

结合炮控系统的实际,系统摩擦力矩动态变化大致可以分为3个阶段,火炮的运动速度ω=0,此时,系统的驱动力矩小于静摩擦力矩,火炮将处于静止状态。当火炮运动速度ω≤ωc时,摩擦力矩较大,为了分析简便,这段区域的摩擦力矩称为静摩擦力矩。当传动轴的角速度ω＞ωc时,系统摩擦力矩下降,这段区域的摩擦力矩称为动摩擦力矩。静摩擦力矩大于动摩擦力矩,两者大小不等,将会对系统产生不利的影响。

根据静态分析,系统需要较大驱动力矩才能克服静摩擦力矩,这样容易造成系统死区,影响系统静态精度;从动态分析看,火炮跟踪低速目标时,如运动速度在 ωc附近时,系统摩擦力矩变化很大,将会造成火炮一时减速,一时停止,一时又加速,周期性跟踪目标,出现低速“爬行”现象。摩擦力矩大小主要与机械传动结构及润滑状况、负载大小和运动速率有关,而且可随着位置和时间而变化。非线性摩擦力矩的存在,将会影响系统的控制精度。

2 系统自适应摩擦补偿控制

设计的交流全电式炮控系统以永磁同步电机(PMSM)为驱动电机,采用速度-电流双闭环的矢量控制结构,使永磁同步电动机的控制与直流电机一样简单。由前文的分析可知,系统非线性摩擦力矩是影响低速性能的主要因素之一。随着炮控系统的运行条件和运行环境的改变,系统摩擦模型也会发生变化,自适应摩擦补偿控制可以计算炮控系统中摩擦模型和控制对象模型参数的变化,能克服由于非线性摩擦和对象模型参数的不确定性对系统造成的影响。非线性摩擦力矩对传动系统的影响主要体现在速度较低的状况[2],因此系统实行分段控制,在速度较低的时候,进行摩擦补偿控制,在速度较高的时候采用PID控制。

系统驱动电机采用id=0的矢量控制策略,系统的输出力矩与电机q轴电流成正比,在系统速度较低时,电机的转速很低,电流频率较低,电机的感性负载可以忽略不计。为了便于分析,将系统电流环简化为一线性放大环节,驱动电机d-q轴模型可以简化为图2。

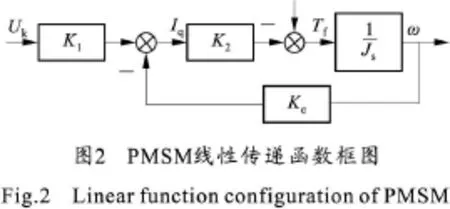
由图3可得系统的动态微分方程为:

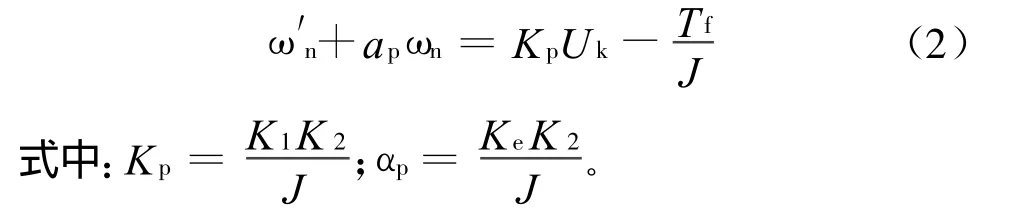
文献[3]和[4]论述了针对转台的Stribeck摩擦模型自适应补偿控制研究,从中可以看出,Stribeck摩擦模型自适应补偿控制算法复杂,用到的变量较多。结合坦克炮控系统特点,从简单适用,便于实现,调试简单的角度出发,本文将探讨简化的Stribeck摩擦模型补偿控制研究。

系统驱动电机采用PWM控制,静-动摩擦力矩之差对系统的影响减弱[5];粘滞摩擦力矩与系统的速度成正比,在摩擦非线性分析时,将其视为线性负载考虑,Stribeck摩擦模型可简化为库仑摩擦模型,库仑摩擦的力矩方程为[6]:

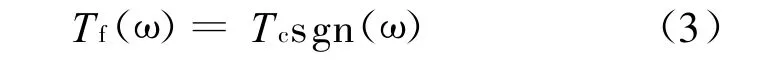
模型参考自适应控制包括:参考模型、对象模型和自适应机构,系统控制结构框图如图4所示。

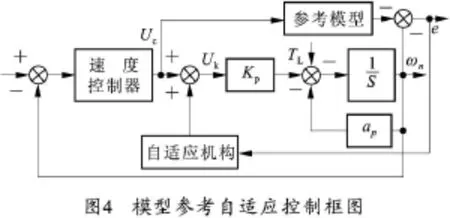
系统的动态方程如式(2)所示,选择渐进稳定的参考模型:

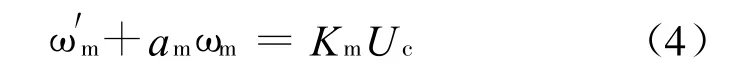
式中,Uc为控制器的输出,根据系统性能指标和参考模型结构,设计出符合要求的控制器。通过模型参考自适应控制器对参数的自适应调整,实现对象输出与参考模型输出保持一致[7]。

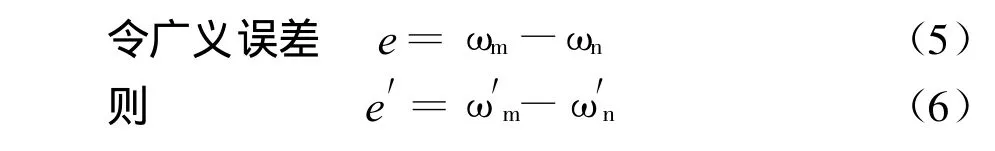
将式(4)减去式(2),并将式(5)、(6)代入后得:

令被控对象的控制输入为:

式中:a1、a2、a3均为自适应可调参数。

将式(8)代入式(7)后得:

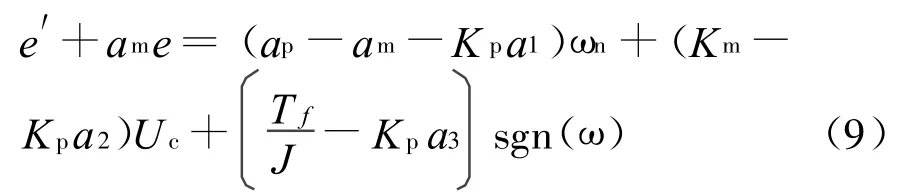
定义自适应控制器的控制向量:

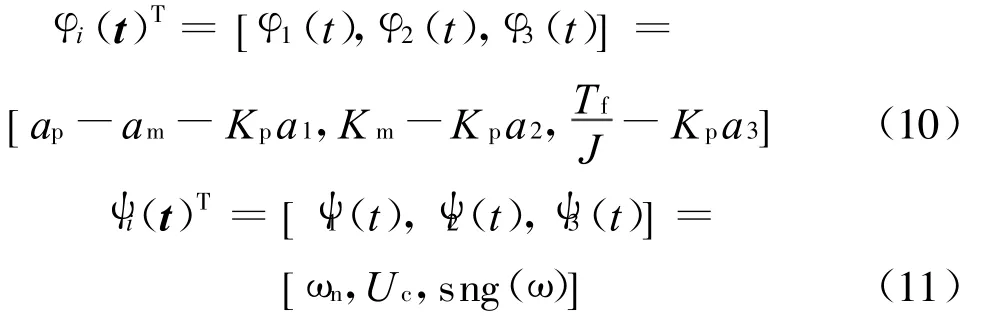
定义李雅普诺夫函数[7]:

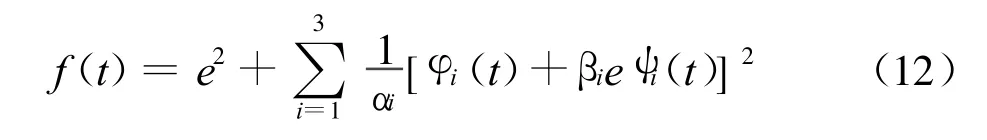
式中 :αi,βi 均为正常数 。

对f(t)求导得:

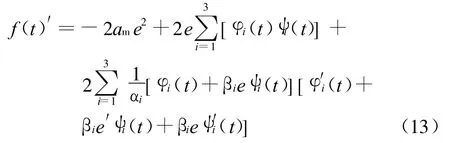
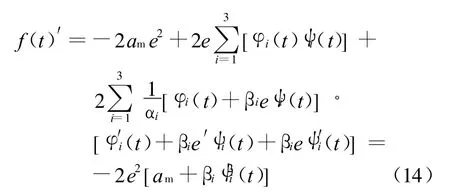
由式(14)可以看出,f(t)′对于所有的e都为负定,根据李雅普诺夫稳定定理,e=0是系统渐进稳定的平衡点,由自适应参数方程:对式(15)两边求导得:

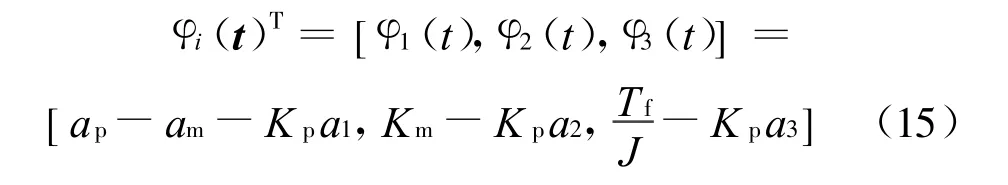
对式(17)两边积分得到参数的自适应调整方程:

由自适应调整方程式(18)可以看出,参数的自适应调整律包含积分和比例两部分,积分部分提供记忆功能,而比例部分是一个瞬态项,αi,βi的选值与参数的自适应收敛速度有关,通过调整a1、a2、a3的值,实现广义误差e→0,即使对象模型输出趋近于参考模型输出。对于该自适应律所用的运算量,系统都能直接获取,利用模型参考自适应控制,可以方便地实现对系统非线性摩擦的补偿控制。

3 仿真分析

上文是基于库仑摩擦模型的自适应补偿控制的分析,该方法采用简单的摩擦模型,具有运算量少,实现方便等优点。针对上文所述的系统非线性摩擦补偿研究,通过仿真考察其对系统性能的改善。仿真中根据实际系统的各项参数,水平分系统参考模型选 ω′m+140.8ωm=19.4U c,α1=0.15,α2=0.1,α3=1,β1=0.01,β2=0.08,β3=0.2,经测量取折算到电机轴的动摩擦力矩 T c=3.4 N◦m。垂直分系统的参考模型取ω′m+8.4ωm=1.38U c,α1=0.08,α2=0.1,α3=3,β1=0.006,β2=0.05,β3=0.6,经测量后取折算到电机轴的动摩擦力矩T c=0.4 N◦m。由于非线性摩擦力矩主要影响系统的低速性能,尤其在运动速度方向改变时,摩擦力矩的非线性表现最为明显,对系统影响最为显著,水平分系统取给定速度为 ωref=2°cos,垂直分系统取给定速度为ωref=2°cos,考察系统的输出波形的正弦跟随特性,系统的仿真波形如图5和图6所示(取稳态的一段)。

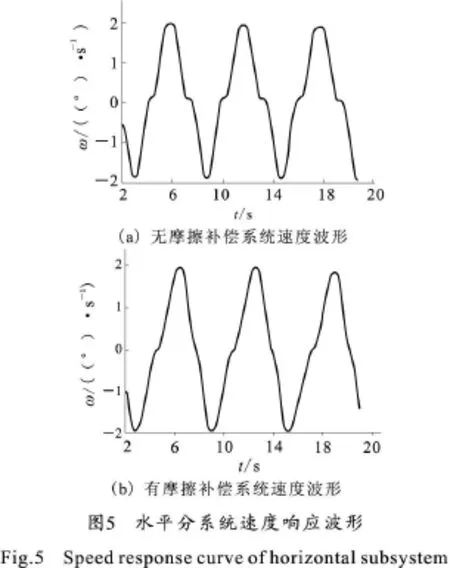
由仿真波形图可以看出,在没有进行摩擦补偿控制以前,由于系统摩擦非线性的影响,速度波形存在明显的“滞缓”现象。采用基于库仑摩擦模型参考自适应摩擦补偿控制以后,系统的摩擦非线性得到了一定的补偿,速度波形中的“滞缓”现象得到了较大程度的缓解,证明了采用模型参考自适应摩擦补偿控制的有效性。

4 试验分析

采用库仑摩擦自适应补偿控制,系统的控制相对简单,在实际系统中,垂直分系统的非线性摩擦力矩表现最为明显,从简单适用,能满足系统的要求出发,本文以垂直分系统为例进行了试验验证,验证摩擦补偿控制的有效性。垂直分系统的参考模型为 :ω′m+8.27ωm=2.82Uc,α1=0.06,α2=0.15,α3=2.6,β1=0.005,β2=0.03,β3=0.5,折算到电机轴的动摩擦力矩T c=0.4 N◦m。取给定速度为:ωref=2°cos,速度响应波形分别如图7和图8所示。

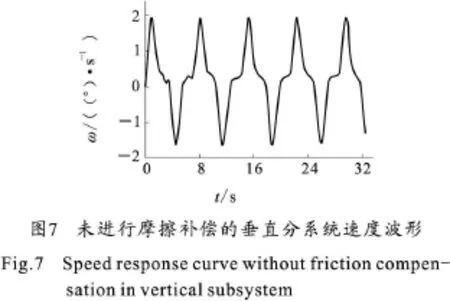
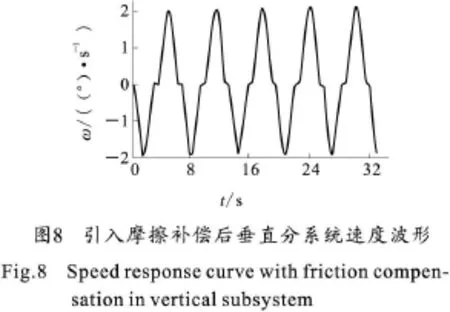
由图7可知,当系统速度方向变化时,由于没有对系统摩擦力矩的突变进行相应的补偿控制,速度波形存在十分明显的“滞缓”现象。图8是引入摩擦补偿后系统速度波形,采用模型参考自适应控制,能及时反应速度变化时系统摩擦力矩的突变,实现对摩擦力矩的补偿控制,所以在系统速度方向变化时,畸变和“滞缓”现象都得到了明显的改善,提高了系统的低速平稳性能。

5 结 论

自适应摩擦补偿控制可以实时计算炮控系统中摩擦模型参数的变化和对象模型参数的变化,能克服系统中非线性摩擦和对象模型参数的不确定性对炮控系统造成的影响。文章设计了基于李雅普诺夫稳定理论的模型参考自适应控制,实现对系统摩擦的补偿控制。仿真和实际应用表明:采用模型参考自适应控制,能够有效地改善系统速度较低时存在的“滞缓”和“爬行”现象,提高系统的低速性能。

[1] 张锦江,陈兴林.基于摩擦自适应补偿的转台变结构控制器设计[J].哈尔滨工业大学学报,2000,32(4):89-95.ZHANG Jin-jiang,CHEN Xing-lin.Design of variab le structure controller based on friction adap tive compensation[J].Journal of H arbin Institute of Technology,2000,32(4):9-95.(in Chinese)

[2] 李书训,姚郁,马杰.基于观测器的伺服系统低速摩擦补偿分析[J].电机与控制学报,2000,4(1):27-30.LIShu-xun,YAO Yu,MA Jie.Analysis of observerbased low-velocity friction compensation in servo systems[J].Electric Machines and Contro l,2000,4(1):27-30.(in Chinese)

[3] 吴南星,孙庆鸿,冯景华.机床进给伺服系统非线性摩擦特性及控制补偿研究[J].东南大学学报:自然科学版,2004,34(6):771-774.WU Nan-xing,SUN Qing-hong,FENG Jing-hua.Study of influence on machine-tool dynam ic characteristics of non linear friction and its compensation[J].Journal o f Southeast University(National Science Edition),2004,34(6):771-774.(in Chinese)

[4] 于志伟,曾鸣,乔大鹏.采用复合控制的直流力矩电机摩擦补偿[J].电机与控制学报,2008,12(15):539-544.YU ZH i-w ei,ZENG M ing,QIAO Da-peng,Hybrid control of friction compensation for DC motors[J].E-lec tric Machines and Control.2008,12(15):539-544.(in Chinese)

[5] KE Jing,SU Bao-ku,ZENG M ing.Robust adap tive fric tion compensation for DC motors with Parametric uncertainties[J].Proceedings of the CSEE,2003,23(7):117-122.

[6] WANG ZH ong-shan,SU Bao-ku,WANG Yi.Observer/filter struc ture based adaptive friction compensation for high precision turntable[J].T ransactions of Nanjing University o f Aeronautics&Astronautics,2008,25(2):113-120.

[7] 陈娟.伺服系统低速特性与抖动补偿研究[D].北京:中国科学院,2001:36-50.CHEN Juan.Study on the low velocity properties and jitter compensation for the servo system[D].BeiJing:Chinese A cademy of Science,2001:36-50.(in Chinese)