某多管火箭炮发射动力学模型 (Ⅰ)

魏孝达,张瑞莎,王惠方

(西北机电工程研究所,陕西咸阳 712099)

多管火箭炮发射与常规火炮有显著区别[1-2]:火箭弹质量大、体积大,它的运动对火箭炮有举足轻重的影响,如某火箭弹质量是单根定向器质量的3倍,是定向器集束的1/4左右,而通常火炮弹丸质量不到炮身质量的1/50,所以在研究多管火箭炮发射振动时应该考虑火箭弹的影响,而在研究火炮时往往可以忽略;火箭弹初速低、定心部之间距离远,造成半约束期的时间长,与炮弹相比,火箭弹半约束期的时间是炮弹的100多倍,说明定向器对后定心部的约束时间较长,使火箭弹离轨时的姿态受到影响;多管火箭炮发射时每发火箭弹的燃气射流冲击力大小和作用点都不一样,并随火箭弹射序的不同而差别很大,这是影响火箭炮振动重要而复杂的因素;火箭炮起落部分为变质量系统,其质量、转动惯量随载弹量多少而不同,并随火箭弹逐一发射而减少。

本力学模型将火箭弹和发射架含在同一个力学系统中,导出了系统动力学方程,提出了火箭弹燃气射流冲击力随压力分布和迎气面积变化的计算方法。模型可以方便地计算火箭弹离轨时刻的空间姿态,分析有关参数(包括发射架结构参数与力学参数、火箭弹推力偏心和质量偏心等特性参数以及发射间隔、发射顺序、发射数量、射向射角等)对火箭弹运动和发射架振动的影响,为多管火箭炮系统优化设计提供理论工具。

建模运用速度矩阵法[3]。先对多管火箭炮进行力学简化,给出力学系统基本假设,通过运动学分析得出系统各刚体的速度、角速度表达式[4],然后建立速度矩阵,得到动力学方程组的系数矩阵,再求出广义主动力,将广义力与系数矩阵相结合,加上辅助方程,即得动力学方程组。

1 基本假设

1)假定多管火箭炮由4个刚体组成,即车体、回转机、起落部分(含摇架、定向器、未发射的火箭弹)和火箭弹(正在发射的1发),见图1。

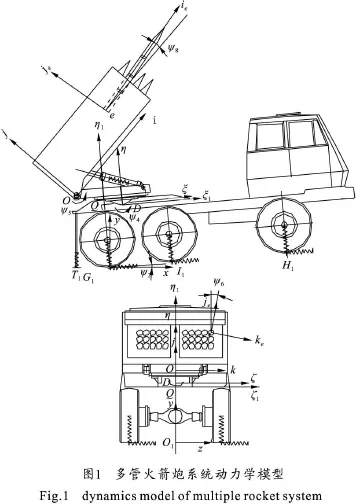
2)炮车作三维空间运动,假定以车体上一点Q为基点,该点相对地面运动的位移量分别用 x、y、z表示,x为Q点的前后水平位移,y为上下垂直位移,z为侧向水平位移;同时车体还绕3个车体坐标系的轴转动,转角用卡尔丹角 ψ1、ψ2和 ψ3表示。

3)回转机绕回转中心D转动,视方向机为弹性元件,其刚度系数可通过“拉力试验”得到,回转机相对车体的转角用ψ4表示。

4)起落部分通过耳轴和高低机与回转机联接,通过高低机使起落部分绕耳轴O转动,视高低机为弹性支撑,其刚度系数可通过“拉力试验”得到,起落部分相对回转机的转角用ψ5表示。

5)假定火箭弹定心部与定向器之间无间隙,在前、中两个定心部离轨前(全约束期),火箭弹相对定向器作直线运动,其直线运动的位移量用x1表示,同时在导向钮的约束下绕弹轴旋转,绕弹轴旋转的转角用ψ6表示,此转角和角速度取决于导向槽的缠角 α和定向器内半径Rd,ψ6=x1tanα/Rd。

在中定心部离轨后火箭弹进入半约束期,此时的火箭弹除相对定向器作直线运动外,还绕后定心部有3个方向的转动,由于绕弹轴的自转受定向钮的约束,故火箭弹只增加2个转动自由度,转角用ψ7和ψ8表示,因此在半约束期,系统简化为11个自由度动力学模型 ,用广义坐标 x、y 、z 、ψ1、ψ2、ψ3、ψ4、ψ5、x1、ψ7和 ψ8描述系统的运动。在全约束期 ,系统简化为 9 个自由度 ,用广义坐标 x、y 、z、ψ1、ψ2、ψ3、ψ4、ψ5和 x1描述系统的运动 。

6)G1 、G2、I1、I2、H1、H2 、T1、T2 分别为后、中、前3对车轮和1对千斤顶的接地点,角标“1”表示右侧,“2”表示左侧,地面反力为车体位移和速度的函数。

2 坐标系

如图1所示,多管火箭炮各特征点定义如下:

O1为地上固定点,选两后轮初始接地点连线的中点;Q为车体上固定点,在O1点正上方的顶甲板平面上;D为回转平面上回转中心点;O为耳轴中心点;e为火箭弹后定心部中心点;q、a、b、c分别为火箭弹、起落部分、回转机和车体的质心;绝对坐标系O1 xyz为固联于地,原点为O1,O1 x轴平行于地面,指向正前方;O1 y轴垂直于地面;O1 z轴平行于地面,指向右方。此坐标架用单位矢量x1、y1、z1表示。

设车体坐标系Qξ1η1ζ1为固联于车体 ,原点为两后轮初始接地点连线的中点正上方的Q点,Qξ1、Qη1、Qζ1轴初始时与 O1 x 、O1 y、O1 z 轴平行,以后随车体运动,此坐标架用单位矢量ξ1、η1、ζ1表示。

回转机坐标系Dξηζ为固联于回转机,原点为回转中心D,Dη轴为回转轴,Dξ、Dη、Dζ轴初始时与Qξ1、Qη1、Qζ1同方向,以后随回转机运动 ,此坐标架用单位矢量 ξ、η、ζ表示。

起落部分坐标系Oijk为固联于起落部分,原点为两耳轴连线的中点O,Oi轴平行于定向器轴线,方向指向管口,发射前为射角方向;Oj轴垂直于定向器轴线,指向上方;Ok轴沿耳轴中心线,指向右方。此坐标架用单位矢量i、j、k表示。

弹体坐标系eie je ke为固联于正在发射的火箭弹,原点为后定心部中心点e,eie轴平行于弹轴,方向指向弹尖,在全约束期,始终与Oi轴平行;eje轴垂直于弹轴,指向上方;eke轴垂直于弹轴指向右方。此坐标架用单位矢量ie、je、ke表示。

为书写简便,令:

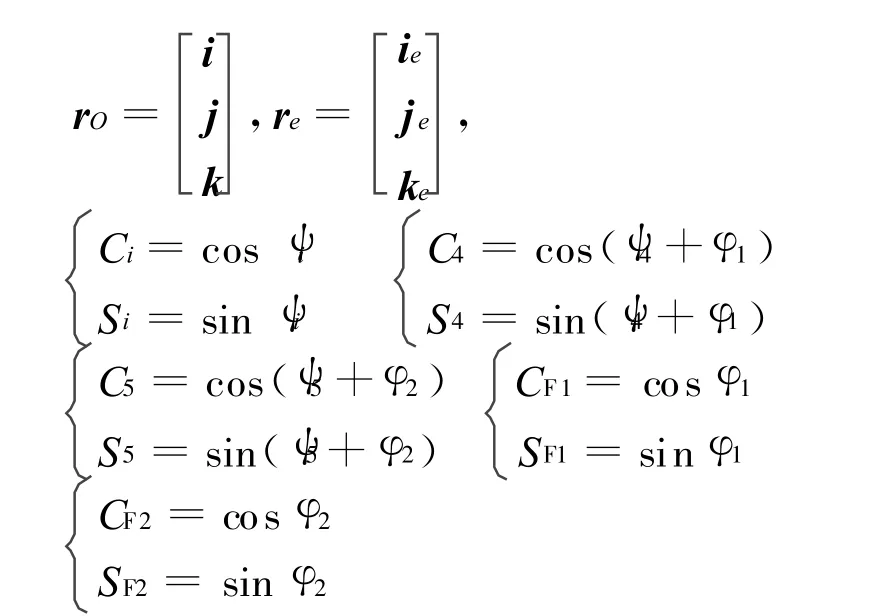
式中:i=1,2,3,6,7,8;φ1为火箭炮射击前赋予的方位角;φ2为火箭炮射击前赋予的高低角。

5个坐标系变换如下:

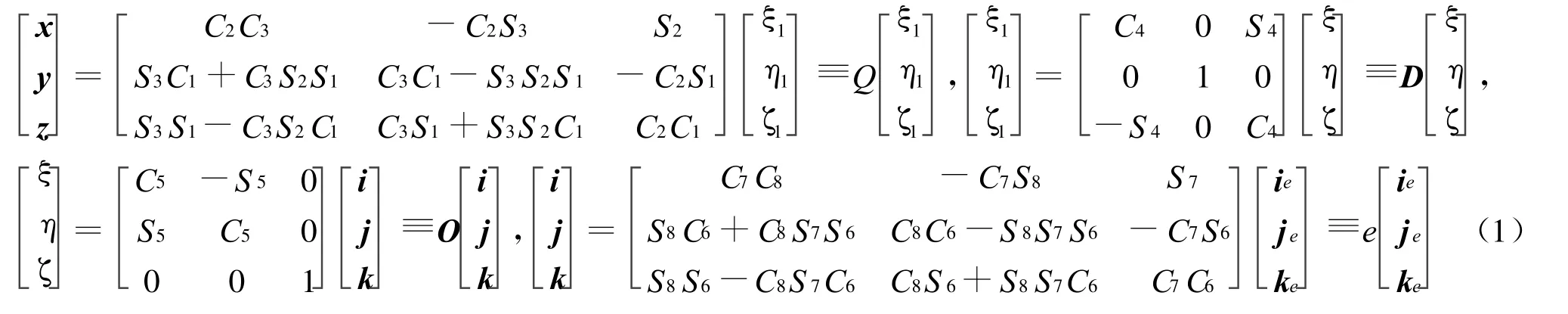
3 各个刚体速度和角速度表达式

1)车体的角速度ω1为:

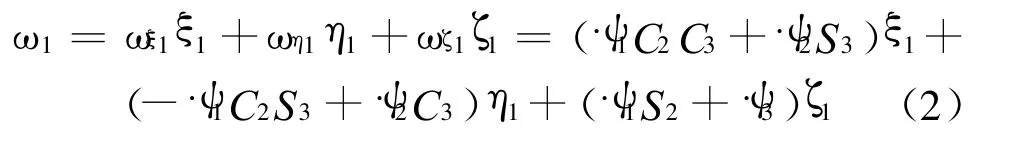
2)回转机的角速度 ω2为:

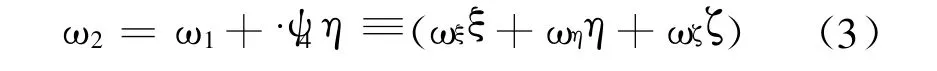
3)起落部分的角速度ω3为:

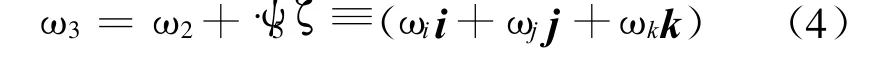
4)火箭弹的角速度 ω4为:

在半约束期:

5)车体坐标原点Q的速度v Q为:

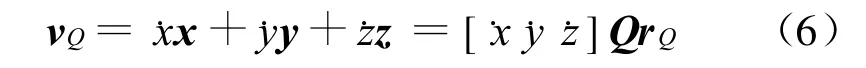
Q为坐标系O 1 xyz变到坐标系Qξ1η1ζ1的变换矩阵,即rO1=Q◦rQ。

6)回转机坐标原点D(回转中心)的速度v D为:

式中,(ξ1D,η1D,ζ1D)为D点在Qξ1η1ζ1 坐标系中的坐标。

7)起落部分坐标原点O(耳轴中心)的速度v O为:

式中,(ξO,ηO,ζO)为耳轴O点在Dξηζ坐标系中的坐标。

8)弹体坐标原点e(后定心部中心)的速度v e为:

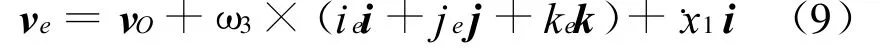
式中,(ie,je,ke)为后定心部中心点e在Oijk坐标系中的坐标。

9)车体质心C的速度v C参照v D为:

式中,(ξ1C,η1C,ζ1C)为C 点在坐标系Qξ1η1ζ1 中的坐标 。

10)回转机质心b点的速度v b参照v O为:

式中,(ξb,ηb,ζb)为炮塔质心 b 点在Dξηζ坐标系中的坐标。

11)起落部分质心a点的速度v a参照v e为:

式中,(ia,ja,ka)为起落部分质心a点在Oijk坐标系中的坐标。

12)火箭弹质心q点的速度vq为:

式中,(ieq,jeq,keq)为火箭弹质心q点在eiejeke坐标系中的坐标。

4 速度矩阵

速度矩阵即各刚体的速度和角速度表达式中每个广义速度前的系数项依次排成的矩阵,由于每个刚体都有3个速度和3个角速度分量,每个速度分量将占矩阵中的一行,每个刚体将占3行,本模型有4个刚体,故速度矩阵为12行;由于每个速度和角速度分量都是11个广义速度的线性组合,它们的系数项要占11列,构成12×11的矩阵。对速度矩阵求导和求偏导即得微分和偏微分矩阵(略)。

5 动力学方程组

系统动力学方程组为:

速度矩阵法阐明,方程式(14)的系数矩阵A、D可用速度矩阵a kmn、b kmn及其微分、偏微分矩阵的元素表示[3],即:

会计委派制是为了强化会计监督，规范会计核算、提高会计信息质量。通过直接委派制，来加强施工企业的财务管理，强化企业的财务监督。委派的财务负责人，是不受项目经理和其他因素控制的，是为了在工程项目的会计核算与财务管理中发挥约束和监督的作用，防止工程项目的经营管理背离公司的管理与经营目标。为此委派财务负责人的工资待遇是由单位支配的，其一是为了有效的保证了对项目经济活动的监督，其二，个人的待遇是与总部财务部的定期考核挂钩，只有这样，会计委派制才会发生作用，才能实现企业的财务监督职责。

式中:i=j=1,2,…,9;Mk为第k个刚体的质量;Jkn为第k个刚体的转动惯量张量分量(k=1,2,…,4;n=1,2,…,6)。

在火箭弹全约束期间,系统为9个自由度;在半约束期间,系统为11个自由度;在前一发火箭弹离轨后、后一发火箭弹启动前,系统为8个自由度;3种情况的方程组不同,需对火箭弹的3个方程作适当取舍,并将舍去自由度的广义速度、广义加速度令成0,无需另行推导方程。

6 广义主动力

6.1 系统作用力

6.1.1 火箭弹推力

发动机推力可以是数组或函数形式,作用于火箭弹,推力存在偏心,假定推力偏心有3种形式,第1种:假定推力方向与弹轴平行,作用点p(iep,jep,kep)偏离弹轴,设推力偏心距为Rp,弹轴与推力作用线构成的平面与j e轴夹角为φ,则jep=Rp cosφ,kep=Rpsinφ;第2种:假定推力作用线与弹轴交于p点,夹角为ψp,p点在弹轴的位置为(iep,0,0),弹轴与推力作用线构成的平面与j e轴的夹角为φ;第3种:假定推力作用线与弹轴既不相交也不平行,设两空间直线的距离为Rp,在过弹轴并与推力作用线平行的平面上,作推力作用线的投影线,此投影线与弹轴的交点位置为(iep0,0),夹角为ψp,弹轴与投影线构成的平面与 j e轴的夹角为φ,同样有jep=Rp cosφ,kep=Rp sinφ的表达式。可见推力的方向和作用点可用4个参数ψp、φ、Rp、iep来确定,不难看出第1、2种形式是第3种形式的特例,若令ψp=0,即第1种形式、令Rp=0,即第2种形式。

存在偏心的推力矢量表达式为:

式中,n为发序,作用位置与射序有关;Pt为推力。

在推力小于闭锁力之前,火箭弹相对定向器不能启动,但系统仍有推力作用,即在除火箭弹外的所有自由度对应的运动方程中,都出现推力生成的广义力;在推力大于闭锁力、火箭弹重力以及摩擦力的合力以后,火箭弹开始在定向器内运动,直到离轨。

若考虑推力偏心的随机性,只要在计算时将ψp、φ、Rp视为随机变量输入即可。

6.1.2 燃气射流冲击力

设第n发火箭弹的燃气射流压强是离喷口距离ies和离弹轴半径r的函数pg(ies,r),ies、r均为t的函数。在每一个垂直于弹轴的截面(ie=ies)上,燃气射流压强按等压圈规律分布[7],也可以用数组形式给出。

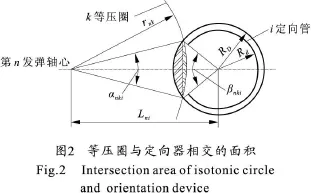
由于火箭弹燃气射流压强以等压圈分布,故需要计算每个等压圈覆盖定向器端面形成的迎气面积:现以第n发火箭弹为中心,画m个压力圈,第k个压力圈外半径为rnk,定向器外半径为RD,第n发的压力圈中心与第i个定向器中心的距离为Lni,第i个定向器中心的坐标用二维数组L(i,j)表示(i=1,2,…,N;j=1,2),i为定向器序号,N为定向器总数,j表示坐标方向,j=1代表k方向坐标,j=2代表j方向坐标。rnk圆与第i个定向器相交构成两个弓形面积Sαki、Sβki,由几何关系 (见图2)得[8]:

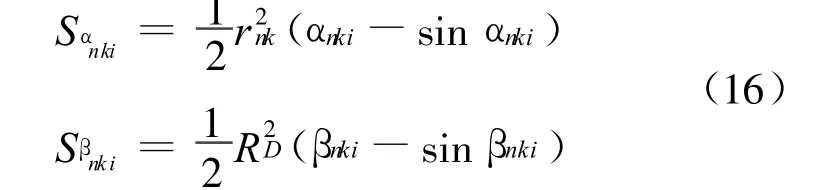
式中:αnki为压力圈中心与两圆交点连线的夹角;βnki为迎气管中心与两圆交点连线的夹角(当 rnk＜β/2为钝角)。

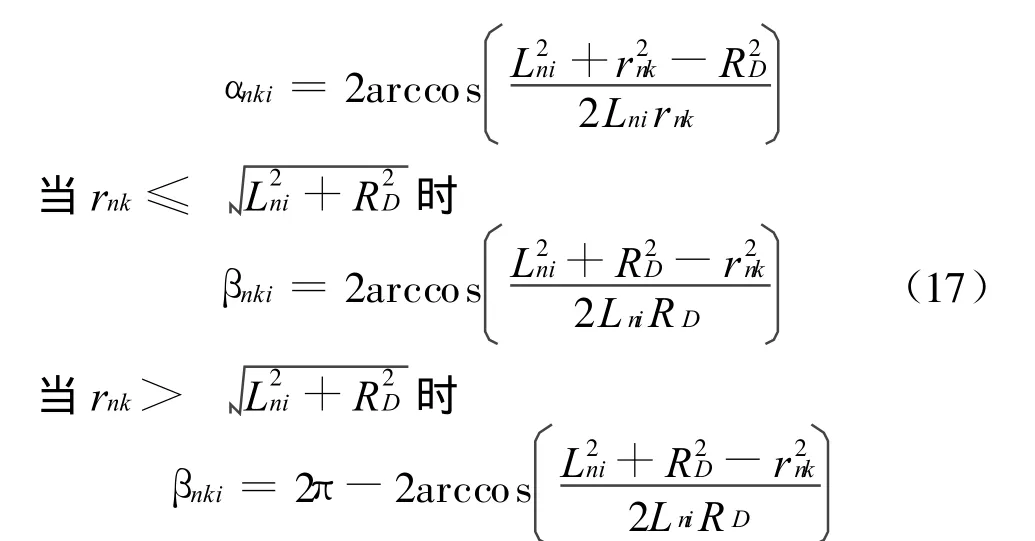
除两圆相交的情形外,还有两种不相交的情形:当 rk ≤Lni-RD 时,Sαnki=Sβnki=0;当 rnk ≥Lni+RD 时 ,Sαnki=0,Sβnki=π。

第n发火箭弹的第k个压力圈与第i个定向器相交的面积为 Snki=Sαnki+Sβnki(k=1,2,…,m;i=1,2,…,N-1),m为设定的等压圈总数,第n发的第k个等压圈交出的总面积为Snki+S0,S0为一个定向器横截面积。第n发的第k个等压圈与第k-1个压力圈之间的环形面交出的面积为ΔSnk=Snk-Snk-1,即得第k个等压环的迎气面积。将第k个等压环的迎气面积 ΔSnk乘以压强pg(ies,rnk)并对k求和,即得第n发火箭弹此刻对所有定向器(实心)的燃气射流冲击力:

式中,Pno为第n发火箭弹自身定向器所受燃气射流冲击力。

由于等压圈半径rnk可以任意选取,所以等压环的大小可以连续变化,燃气射流冲击力可写成积分表达式,得到更精确的计算结果。

以上得出的是对未发射的定向器(实心)的迎气面积,对发射后的空管迎气面积只要减去管内部分,空管用同样方法计算,只需把定向器外半径RD改为内半径Rd即可,见图3。

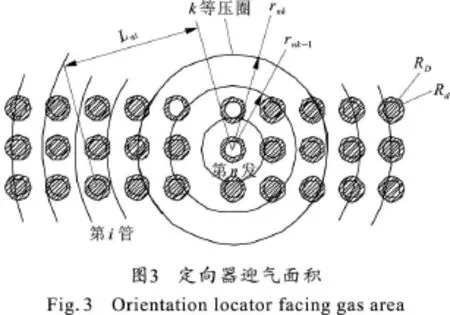
整个定向器集束的迎气面积,还应考虑它的结构特点,如定向器用隔板固定,则应计算前隔板的迎气面积,算法可将整个隔板的长方形迎气面积减去当前的空管面积来实现。设长方形前隔板面上第n发定向器中心至4边的垂直距离依次为Ln01≤Ln02≤Ln03≤Ln04,至4个顶点(编号为5,6,7,8)的距离依次为Ln05≤Ln06≤Ln07≤Ln08,为求整个长方形面上的受力,先算第n发定向器中心为圆心以r为半径的圆与长方形交成的面积Sn(见图4)。

为分析计算简洁,将 Ln0i(i=1,2,3,4)、Ln0 j(j=5,6,7,8)合在一起再排队,得 Ln01≤Ln02≤…≤Ln07≤Ln08,这就把r分成8个区间来描述交成的面积Sn,例如可能排成 Ln01≤Ln02≤Ln05≤Ln03≤Ln06≤Ln04≤Ln07≤Ln08,其他所有排列都遵循以下相同规则:

有:

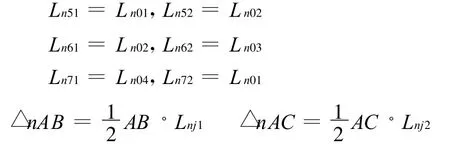
其中:

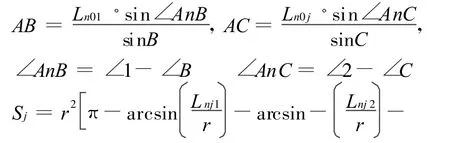
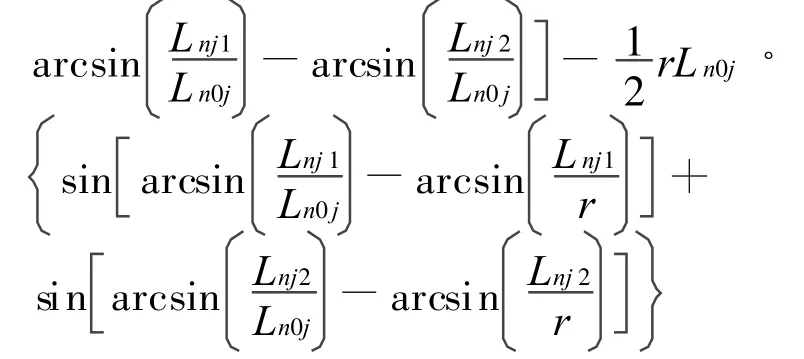
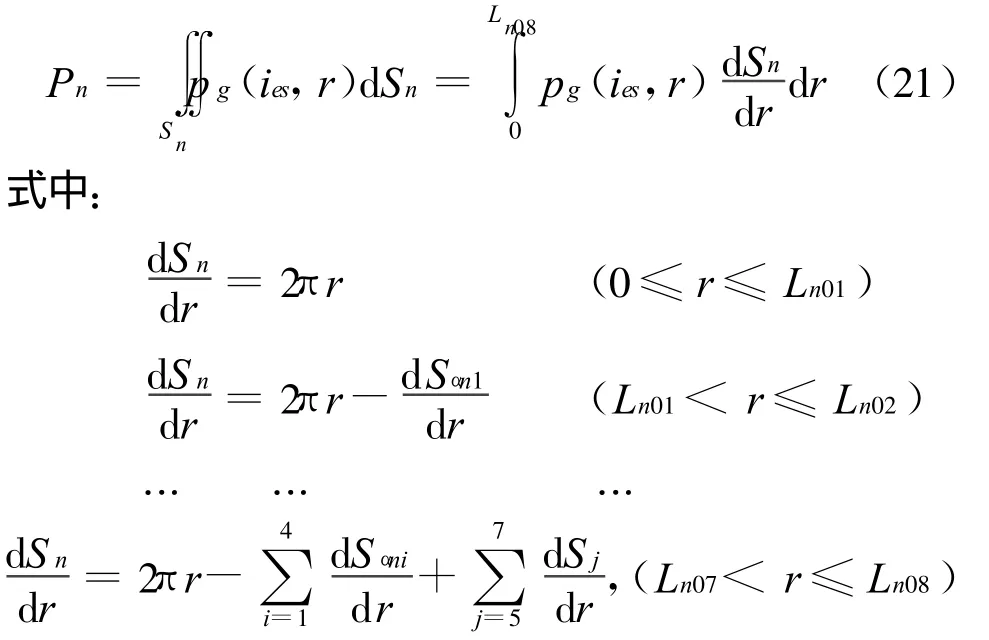
隔板面上的燃气射流冲击力,即长方形迎气面上的力减去空孔面上的力;作用在车体等其他地方的燃气射流冲击力比较小,需要考虑的话可用其投影面作为等效长方形迎气面进行估算。(待续)

[1] 朱怀亮,张福祥.刚柔耦合下火箭炮多体系统的动力建模方法探讨[J].火炮发射与控制学报,1995(2):8-13.ZHU H uai-liang,ZHANG Fu-xiang.Investigation on launchermulti-part system dynam icmodeling under rigid and f lexib le coup ling conditions[J].Journal o f Gun Launch&Control,1995(2):8-13.(in Chinese)

[2] 芮筱亭,陆毓琪,王国平,等.多管火箭发射动力学仿真与试验测试方法[M].北京:国防工业出版社,2003.RU I Xiao-tin,LU Yu-qi,WANG Guo-ping,et al.Simulation and testmethods of launch dynam ics ofmu ltiple launch rocket system[M].Beijing:National Defense Industry Press,2003.(in Chinese)

[3] 魏孝达,崔青春,张瑞莎.任意正交坐标系下的速度矩阵法[J].火炮发射与控制学报,2005(4):4-9.WEIXiao-da,CUIQing-chun,ZHANG Rui-sha.Velocity matrixmethod of arbitrarily coordinate system[J].Journal of Gun Launch&Control,2005(4):4-9.(in Chinese)

[4] 洪善桃.高等动力学[M].上海:同济大学出版社,1990.HONG Shan-tao.Higher Dynam ics[M].Shanghai:Tongji University Press,1990.(in Chinese)