基于LS估计检测QRS波群宽度
王大雄 蒋云良 徐 耕 申 情
1(湖州师范学院信息工程学院,湖州 313000)
2(浙江大学医学院附属二院,杭州 310006)
引言
心电信号在临床诊断和生理研究中具有重要价值。波形检测识别和参数提取是心电信号处理的核心,其准确性和可靠性决定了诊断的效果,目前国内外学者就QRS波群的位置检测识别已经做了较充分的研究,形成了很多检测算法[1-2],但就QRS波群的重要参数、QRS波群宽度的提取尚少有研究。而QRS波群宽度的检测是ECG形态分析中的首要问题,在心电图的临床医学诊断中,医生常据此并结合P波和T波分析病人的心律失常[3],在心电监护仪器的监护中也是如此[4]。QRS波群宽度正常约0.06~0.1 s,0.1~0.12 s常提示为预激综合症或室上性早搏,超过0.12 s的QRS波群宽度常提示为室性早搏或伴差异传导的室上性早搏。
本研究提出一种检测心电图QRS波群宽度的新方法:在检测出QRS波群并确定任意一点在QRS波群内的基础上,以所确定的点为基点,向前和向后逐段求出线段参数的LS估计,并求出线段的线性度;根据LS估计和线性度确定基线,在此基线上再利用假设检验的方法得出QRS波群的起点和终点,从而提取了QRS波群宽度这一特征参数。该方法在正常和倒置QRS波群、具有高大T波和带倒置T波的 QRS波群、有严重基线漂移和严重噪声的QRS波群等的检测都获得成功,并成功应用于具有广泛认可度的MIT-BIH数据库的心电数据,具有广泛的适用性和良好的稳健性、较强的抗噪声能力和抗基线漂移能力,达到了较高的检测精度。该方法计算量小,运行速度快,精度高,适于实时检测,并且宽度的检测结果与QRS波群内选取的基点位置无关。
1 QRS综合波波宽检测算法原理
在心脏的心电空间向量环理论中,在心房兴奋的P环到心室兴奋的QRS环之间有一等电位水平线T1,在QRS环到心室复极向量环T环之间亦有一等电位水平线T2。虽然由于基线漂移的原因导致T1和T2并非水平,但由于基线漂移相对于 QRS波群的运动较缓慢,还由于这两段时间持续极短,所以T1和 T2的线性度远高于 QRS波群的线性度。正常QRS波群持续时间为0.06~0.1 s,异常 QRS波群持续时间鲜有超过0.2 s。设心电数据采样周期为 Ts,心电数据为{z(n)},已经确定 z(k)为 QRS波群的任意一点,求 QRS波群的终点,可以表述如下:
以z(k)为基点,向后选取M+N长度的数据以包含QRS波群的终点;选择线段长度为 T,其长度小于T1的长度,也小于 T2的长度。记 N=[T/Ts]+1,有
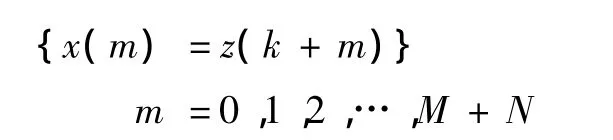
现在的问题是:求出 p,使 x(p)为 QRS波群的终点。
对于求QRS波群的起点,可类似表述为
以z(k)为基点,向前选取长度为M+N时间的数据,以包含QRS波群的起点,有

现在的问题是:求出 q,使 y(q)为 QRS波群的起点,所以求QRS波群的起点和终点,可以用同样的方法进行。下面以求 QRS波群的终点 x(p)为例,阐述算法原理。
若x(p)为QRS波群的终点,记有序集 A和 B分别为
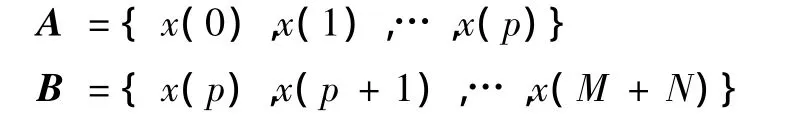
则有序集A是QRS波群数据集合,有序集B的前面是QRS波群后的等电位线T2的数据集合。
现在要找出两者的差别,以确定分割点p。
在T2上任取一段 T,T 式中:d(n)为非随机的序列,是x(n)的均值部分;v(n)是均值为零的平稳时间序列,是x(n)的随机变化部分,又称为余差为共轭序列。 因为按定义T1和T2都是线性度很高的线段,所以可以认为d(n)具有如下形式,即 记 则 X=φα+V 记B=(B(i-j))表示由v(n)的协方差函数构成的 N ×N 矩阵,设 B、φτB-1φ 都满秩,则由(X -φα)τB-1(X -φα)=min可以求得 α 的最小方差线性无偏估计,即 因为此线段在等电位线上,可以确定它的线性度是较高的,也就是 e(p+j)的值较小。显然,若 e(p+j)的值为零,则此线段是完全线性的。 将以上估计以T长度(即N点数据)延伸到所选取的所有数据,也就是对所选数据有 以m=0至N-1为第一条线段 L0,m=1至 N为第二条线段L1,…,以m=M+1至 M+N为最后一条线段LM+1,求出每条线段的LS估计^αLS和线性度e。这些线段要么完全在等电位线上,要么不完全在或完全不在等电位线上。后者必然部分或全部在QRS波群或者T波上,它们的LS估计和线性度与完全在等电位线上线段的LS估计和线性度必然有显著差异。这些差异显著地表现在两个方面:一为线性度较低,或者e值较大;二为LS估计中的斜率估计值较大。 所以,搜索QRS波群的终点p的算法如下: 记 emin=min{e(0),e(1),…,e(M+1)},有序集合 L={L0,L1,…,LM+1},H1、H2、H3为设定阈值。H1和H3的设定与信号的采样频率有关,当采样频率较低时,相邻两点的差就会大些,此时的设定值就可大些,反之则小些;H2可以设置为一个合适角度的斜率。 1)以容许线性度 emin+H1分割有序集 L,得两个有序集La和Lb。其中,La所含线段的线性度均小于容许线性度,Lb所含线段的线性度均大于或等于容许线性度。 2)在有序集 La中求出最平坦线段的斜率 LS估计,记为amin。以容许斜率 amin+H2分割有序集La得有序集 La1和 La2。其中,有序集 La1中每条线段的斜率LS估计均小于容许斜率,La2所含线段的斜率LS估计均大于或等于容许斜率。 3)有序集La1中的线段都在等电位线中,取序号最小的线段,也就是有序集 La1中的第一条线段。此线段必然也在等电位线上,记此序号为Q,则该线段为 LQ。 4)但是,点x(Q)并不一定是QRS波群的终点,记LQ上的估计值和真实值的最大绝对偏差为MX=max{|x(Q+i)-a(Q)×i-b(Q)|:i=0,1,…,N-1}。将线段LQ向小序号方向延伸,即以j=0,1,2,…计算 C(j)=|x(Q-j)-a(Q)×(0-j)-b(Q)|,记J为第一个满足C(J)≥MX+H3的点x(Q-J),使用假设检验法,判定 x(Q-J)已经在显著水平上不在线段LQ上。因为基点在QRS波群内,同时假设检验在线段LQ上向小序号方向延伸,所以可认为x(Q-J)在QRS波群上;因为 x(Q-J)为第一个偏离LQ的点,所以可认为x(Q-J+1)是 QRS波群的终点;因为QRS波群的终点在QRS波群和等电位线的相交处,从而得到终点x(p)和它的位置p=Q -J+1。 5)用同样的方法,可以得到QRS波群的起点y(q);按照x(p)和y(q)的定义,可以得到QRS波群的宽度=(p+q)Ts,Ts为采样周期。 算法是在MATLAB平台上实现的。首先进行定性分析,将此算法应用于所搜集的各种形态QRS波群,以及来自 MIT-BIH数据库编号为108、609和118E24心电数据中的 QRS波群。编号为118E24的数据是叠加噪声的心电数据,108、609和118E24的噪声均较大。选取的心电数据中含有严重基线漂移,包含的QRS波群有正常的、带高大T波的、倒置的和带倒置T波的。使用垂直线,在心电图中标注检测到的QRS波群的起始点和终末点。 对于宽度的检测结果与QRS波群内选取的基点z(k)位置k无关这一点也做了实验。对同一个QRS波群,选取QRS波群内的不同位置为基点,所检测出的QRS波群的起点和终点的位置完全相同。从理论上来说,以检测终点为例,选取较小的基点k,将使数据{x(m)=z(k+m):m=0,1,2,…,M+N}含有更多的QRS波群的数据。选取较大的基点k,将使数据{x(m)=z(k+m):m=0,1,2,…,M+N}含有较少的 QRS波群的数据。无论何种情况,所增加或减少的T长度N点的线段都是些线性度较低(e值较大)或是LS估计中斜率估计值较大的线段,最后都将在有序集的分割中筛去,是不影响QRS波群的终点的检测的,实验也证明了这一点。 为对算法做定量分析,选取了具有QRS波群起始点和终末点标记的QT数据库,该数据库共有105个数据文件,每个数据文件有两道心电信号,每道心电信号持续时间均为15 min,采样频率均为250 Hz,也就是每个点为4 ms。数据库中对心电信号QRS波群的起始点和终末点的标记有两组标准:第一组为q1c,是每个数据文件都有的,在每个数据文件中的持续15 min的心电信号中,选取30个或以上的QRS波群进行标记,共标记了3 623个QRS波群,称为 ref1;第二组为 q2c,只有11个数据文件具有,标记的QRS波群为404个,称为ref2。为能与其他研究者的结果[6]比对,也采用了数据库中的全部105个数据文件,并采用了相同的11个数据文件,编号分别为 sel100、sel102、sel103、sel114、sel116、sel117、sel123、sel213、sel221、sel223、sel230,其中ref1标记的QRS波群为487个,ref2标记的 QRS波群为404个。 两组标准是有区别的,其区别如表 1所示[6]。计算方法如下:以起始点为例,对同时具有ref1和ref2标记的404个QRS波,因为两者标记的起始点一般不同,计算其误差,这些误差的平均值就是 m,根方差就是s。 表1 ref1和 ref2的区别(m±s)Tab.1 The differences between ref1 and ref2(m±s) 进一步的研究表明,即使是同一标记标准下同一个心电信号中的两个基本形态类似的QRS波群,其标记也存在明显的差异,所以可以认为,与标准比较的误差的平均值和根方差只要在一个足够小的范围内就可以了。 WT方法[6],对有 ref1和 ref2标记的 QRS波群进行了实验,并计算了实验结果,与 ref1、ref2的误差的平均值m和根方差 s,而本研究也进行了同样的操作,并且将所得结果与 WT方法的结果[6]进行了比较。在使用本算法处理前,没有对任何数据文件进行诸如平滑等任何预处理。 各种形态QRS波群的宽度检测结果如图1所示。 图1中(f)和(h)的心电数据的采样频率为360 Hz,其他心电数据的采样频率均为250 Hz。图1中(f~(h)依次为 MIT-BIH数据库的编号为108、609和118E24的心电数据。每个子图中有两条垂直线,第一条标出检测出的 QRS波群起点位置,第二条标出检测出的QRS波群终点位置。可以看出,对正常的QRS波群、带高大 T波的 QRS波群、倒置的QRS波群、带倒置T波的QRS波群、有严重基线漂移的QRS波群和噪声严重的QRS波群,该算法都能准确地检测出QRS波群的起点和终点位置,从而准确地计算出QRS波群的宽度。 定量分析实验结果如表2所示。可以看出,使用LSE方法所求的QRS宽度的精度较WT方法提高较大,而这也是本研究的目的所在。误差的根方差s均小于或等于WT方法,只是QRS终末点的误差平均值要稍大于WT方法,但是也保持在一个足够小的范围内,达到了较高的检测精度。 表2 LSE和WT在ref1和ref2标准下的比较 (m±s)Tab.2 The comparison between LSE and WT based on ref1 and ref2(m±s) 目前,心电图QRS波群宽度检测的研究已经展开[7]。从实验结果来看,本方法能适用于各种形态的QRS波群,即正常和倒置 QRS波群、具有高大T波和带倒置T波的QRS波群、有严重基线漂移和严重噪声的 QRS波群等,具有广泛的适用性;具有较高的检测精度,检测精度已经达到了一个采样点(4ms)的数量级;在含有噪声大、基线漂移严重的QRS波群中仍然达到了较高的检测精度,具有良好的稳健性和较强的抗干扰性。此外,由于WT方法需要先对心电数据进行小波变换,而本方法则不需要,所以就算法的时间复杂性而言,本方法要远低于WT方法,或者说,本方法相较WT方法要快得多,可以用来对心电信号进行实时处理,这已经得到了验证[4]。该方法计算量小、运行速度快,适于实时检测,为解决非人工交互的实时心电图计算机自动诊断打下了坚实的基础。 图1 各种形态QRS波群的宽度检测结果。(a)正常QRS波群,波宽 =0.076 s;(b)异常QRS波群1,波宽 =0.096 s;(c)异常 QRS波群2,波宽 =0.124 s;(d)异常 QRS波群3,波宽 =0.128 s;(e)异常 QRS波群4,波宽 =0.152 s;(f)异常QRS波群5,波宽 =0.097 s;(g)异常 QRS波群6,波宽 =0.148 s;(h)异常 QRS波群7,波宽 =0.139 sFig.1 The detection results of QRS complex width in various patterns.(a)normal QRS complexes:width=0.076 s;(b)abnormal QRS complexes 1:width=0.096 s;(c)abnormal QRS complexes 2:width=0.124 s;(d)abnormal QRS complexes 3:width=0.128 s;(e)abnormal QRS complexes 4:width=0.152 s;(f)abnormal QRS complexes 5:width=0.097 s;(g)abnormal QRS complexes 6:width=0.148 s;(h)abnormal QRS complexes 7:width=0.139 s [1]Shubha Kadmbe. Wavelettransform-based QRS complex detector[J].IEEE Trans Biomed Eng,1999,46(7):838-848. [2]李翠微,郑崇勋,袁超伟.ECG信号的小波变换检测方法[J].中国生物医学工程学报,1995,14(1):59-66. [3]张文博,徐成斌,强瑞春.如何分析心律失常[M].北京:人民卫生出版社,1982. [4]王大雄,王国钧.基于嵌入式微机的便携心电监护仪设计[J].航天医学与医学工程,2005,18(3):196-200. [5]复旦大学编.概率论第三册随机过程[M].北京:人民教育出版社,1981. [6]Martinez JP,Almeida R,Olmos S,et al.A wavelet-based ECG delineator:evaluation on standard databases[J].IEEE Trans Biomed Eng,2004,51(4):570- 581. [7]夏恒超,詹永麒,杨海威.基于小波变换和移动窗口积分函数的心电信号的QRS波起、终点的检测[J].上海交通大学学报,2002,36(12):1750-1753.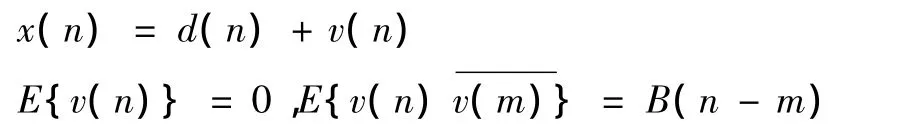
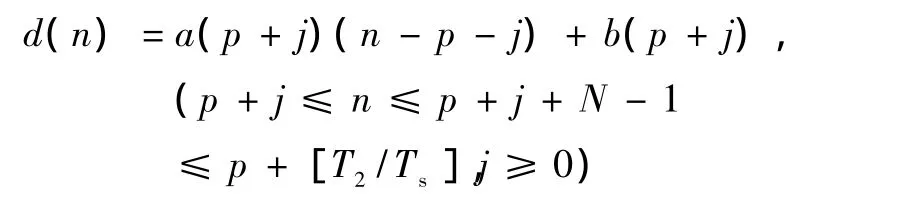




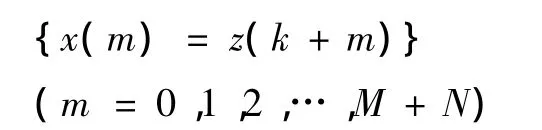
2 算法验证方法

3 结果

4 讨论和结论


