三体船操纵特性计算机数值仿真

卢晓平 姚 迪 王 中

1海军工程大学 船舶与动力学院，湖北 武汉 430033

2大连船舶重工有限责任公司军事代表室，辽宁 大连 116000

三体船操纵特性计算机数值仿真

卢晓平1姚 迪2王 中1

1海军工程大学 船舶与动力学院，湖北 武汉 430033

2大连船舶重工有限责任公司军事代表室，辽宁 大连 116000

以三体船水动力型和K、T响应型（线性和弱非线性）操纵性运动方程为理论基础，以三体船重心运动轨迹微分方程组为数值仿真基础，采用仿真计算工具Matlab软件，对三体船回转运动轨迹、操纵性曲线以及Z型操纵试验曲线等操纵运动特性诸元进行了仿真计算。通过和单体船的对比分析，所得出的计算结果比较合理，计算结果显示三体船较单体船定常回转特性有所下降，而直线稳定性有所加强，跟从性和转首性有所提高。

Hess-Smith法；细长体理论；切片法；操纵性；三体船

1 引 言

三体船型具有良好的耐波性和稳性，同时，在一定速度区间，拥有阻力性能好以及甲板面宽敞等优点。澳大利亚在2005年建造完成了世界最大全铝质车—客—货运三体船，船长约127 m，500 t装载下可达航速40 kn。2008年，美国建造完成三体濒海战舰“独立”号，其航速达到45 kn。这两艘大型三体船建造完成，标志着国外当代三体船即将进入商业应用和军事应用时期。三体船水动力研究也得到较为广泛地开展［1］，而三体船操纵性的研究则十分薄弱。文献［2］对三体护卫舰一个方案设计的操纵性略有涉及，给出了三体船与单体船回转性能对比的初步结果。意大利船舶研究中心（CETENA）对常规单体运输船舶操纵性模拟程序SIMUP进行适当修改后，应用于三体船操纵性能的预报，计算了不同侧体布局的三体船的回转运动和Z形运动，考察了不同侧体纵向位置对三体船航向稳定性和回转性能的影响［3］。中国在三体船操纵性方面的研究，主要包括操纵性水动力导数的经验公式推广应用、水动力导数的理论计算、三体船操纵特性数值仿真初步研究［4-5］等。除此之外，三体船的操纵性研究的文献就鲜有报道。作为新型高性能船型的一种重要航海性能，有必要进一步深入开展三体船的操纵性研究。

本文基于文献［4，5］研究，以三体船水动力型和线性、弱非线性K、T响应型操纵性运动微分方程为数学模型，以三体船重心运动轨迹微分方程组为数值仿真基础，采用仿真计算工具——Matl a b软件，对三体船回转运动轨迹、操纵性曲线以及Z型操纵试验曲线等操纵运动特性诸元进行了数值仿真，并据数值仿真结果对三体船的操纵特性进行了分析。

2 数学模型

2.1 坐标系

为了建立舰船操纵运动方程式，采用如图1所示的两个右手直角坐标系，其中O0x0y0z0为固定坐标系，Gxyz为随船坐标系。Gxyz原点取在主船体水线面对称线的中点（船中处），并假设该点与重心G重合。在舰船操纵性水动力导数计算中，通常采用如图1所示的随船坐标系中的运动方程，而在舰船运动轨迹仿真计算中，需要用到固定坐标系O0x0y0z0。

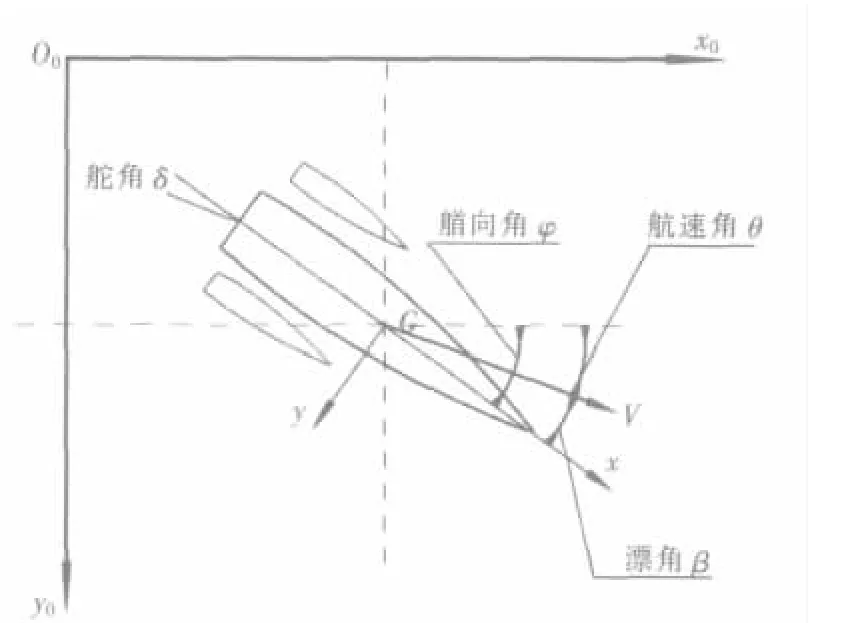
图1 描述三体船运动的坐标系

2.2 操纵运动方程

基于操纵性MMG分离模型，通过O0x0y0z0与Gxyz坐标变换关系以及近似处理，可以得到随船坐标系下的舰船操纵运动线性化方程，如式（1）所示：

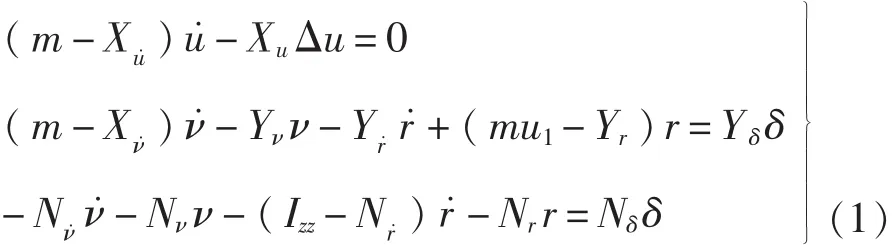
在工程实用中，往往更关注艏向角φ及其角速度r随时间变化的规律。对于一般的船舶，由于操舵速度是有限的，且船舶本身的惯性很大，对舵的响应基本是一种缓慢运动，在操舵不是很频繁的情况下，由线性化的水动力模型可以导出关于r的一阶方程：

式（2）也称为“野本”（Nomoto）方程，式中：

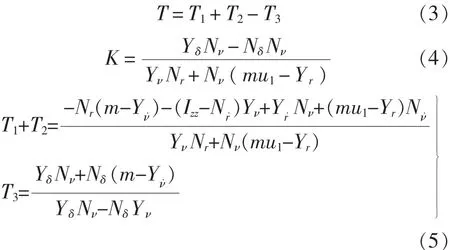
与野本（Nomoto）方程相对应的二阶线性响应模型［6］为：

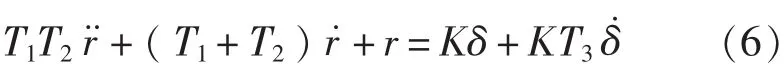
该方程可以在“线性平均”的意义上用于描述中等幅度的操纵运动，方程中隐含的流体动力导数不再是ν，r为零时的流体动力曲线的斜率，而是运动状态为ν，r时，有关动力曲线的斜率。野本提出对式（6）略加修正后得弱非线性二阶响应方程［7］，可以写作：

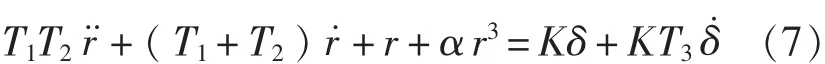
自然，在非线性二阶情况下，各种线性流体动力导数将依赖于r变化，非线性影响由αr3体现，α是新引入的常数，而K，T1，T2和T3应由对应于很小的r的线性流体动力导数加以计算。类似于线性化一阶KT响应方程，式（7）可以简化为弱非线性一阶KT响应方程，即

式（7）、式（8）中的系数α可通过螺旋试验结果予以确定，此时式（8）需进一步简化为定常回转下相应的表达式：

应用最小二乘法据螺线试验曲线或水动力数值计算所得r与δ对应关系进行曲线拟合，就可确定 α 或 α 与 K。在式（4）、式（5）中还含有各种操纵 性 水 动 力 导 数 Xu˙、Xu，Yν、Yν˙，Yr、Yr˙，Nν、Nν˙，Nr、Nr˙，Nδ、Yδ等，均为通常含义下的水动力导数，具体含义参见文献［8］。

以上各种操纵性水动力学方程和响应方程形式的数学模型可直接用于三体船操纵特性预报，也是三体船操纵运动动态特性计算机数值仿真的基础。三体船操纵性预报与操纵运动计算机仿真并无绝对的分界，只是三体船操纵运动计算机数值仿真强调对三体船操纵运动轨迹、Z型操纵试验曲线等，具有时域特点的动态过程进行计算机模拟。所以，三体船操纵运动计算机数值仿真的数学模型应在操纵性预报数学模型基础上，附加求解三体船运动轨迹的微分方程组，或特指求解三体船运动轨迹的微分方程组。

2.3 操纵运动计算机数值仿真模型

如上所述，将三体船计算机数值仿真理解为三体船操纵运动轨迹、Z型操纵试验曲线以及其他操纵运动参数随时间变化曲线等，具有时域特点的动态过程计算机数值模拟。此时计算机数值仿真的项目应包括三体船运动轨迹、Z形操纵试验曲线、速降随时间变化的曲线等。

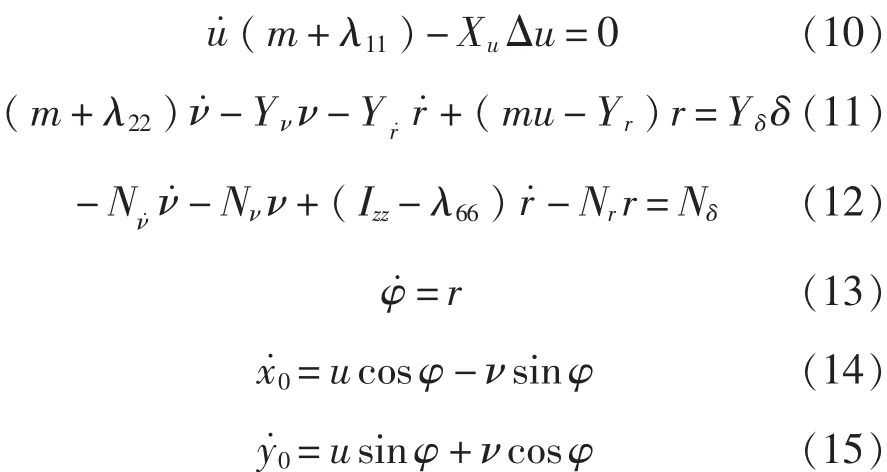
式（10）～式（12）中，λ11、λ22分别为 x、y 轴方向的附加质量，与-Xu˙、-Yν˙相当；λ66为绕 z轴附加惯性矩。联立求解式（10）～式（15）即可以求出各种舵角下的三体船（重心）运动轨迹。

式（10）是独立的方程，由此式可以解出u。通常认为在直线航行状态u的变化不大，近似取为常数；而在定常回转下u自然也是常数；只是在转舵初始到定常回转之间的过渡状态，u的变化才较为明显。但回转中过渡状态的u即使按式（10）计算也与螺旋桨的工作状态有关，且不容易准确求出，故在以下对目标船型回转运动轨迹的数值仿真计算中，据定常回转下速降公式以及模型试验资料建立的u近似计算公式，以该近似公式取代式（10）与其他各式联立求解回转运动的轨迹。本文采用前苏联的费尔索夫提出的定常回转速降公式：

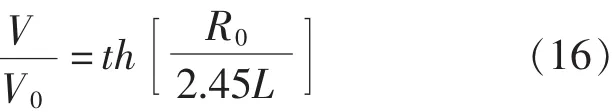
式中，V0和V分别为直线航行速度和定常回转速度；R0为定常回转半径。

按上式求出V后，进一步给定速降时间和u随时间变化的函数模态即可得出u的经验公式。据模型试验和数值仿真计算资料，本文假设u随时间变化的函数为以下3次函数：

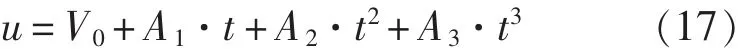
据文献［7］给出的几组速降仿真计算曲线和试验曲线模态，对一目标船型TR3800确定式（17）的各系数如表1所示。表1中的速降时间需参照回转运动船体重心轨迹通过迭代计算确定。迭代计算过程如图2所示。

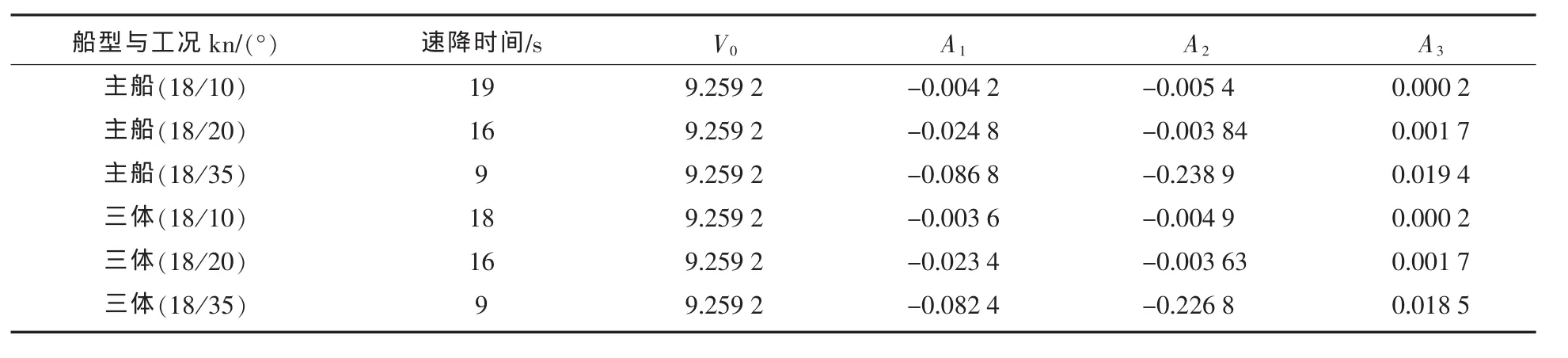
表1 TR3800船型回转过程速度变化函数表达式系数

图2 速降时间计算的一种迭代过程

螺旋试验曲线（操纵性曲线）尽管不是时域特性曲线，但属于动态过程曲线，且是描述操纵运动特性的重要资料，本文也将其列入数值仿真的项目。此时按式（8）、式（9）计算确定螺旋试验曲线。

2.4 三体船的“三体”问题处理

对三体船而言，数学模型中还隐含了对“三体问题”的处理，具体来说“三体问题”的处理隐含在数学模型中出现的水动力导数计算中。本文的处理方法如下：

1）采用三片体分离模型（即MMG模型）的总体思路处理三体问题；

2）由于坐标系原点取在主船体水线面的中点（1／2船长处），故在侧体力矩类水动力导数计算中，需要变换坐标（即惯性矩以及力矩移轴定理应用）；

3）片体间存在一定的水动力干扰作用，需对其影响大小进行分析或计入该项影响。

作者所在的课题组研究表明，三体船片体间水动力干扰作用对三体船操纵运动附加质量、附加惯性矩有一定的影响，但影响不大，如图3～图5所示。这组图谱引自课题组对三体船TR3800研究的结果，图中横轴、纵轴分别代表 a／L、p／L，即片体纵向偏距、横向偏距与船长之比；等值线数值表示三体船3种附加质量（附加惯性矩）与相应单片体附加质量（附加惯性矩）之和的比值。将传统的切片法或细长体理论［9］推广按MMG思路计算三体船水动力导数不便于计入片体间的水动力干扰，此时可按图3～图5这一类三维面元法计算结果对片体间水动力干扰进行修正，或不计片体间水动力干扰。按三维面元法确定水动力导数则可自动计入片体间的水动力干扰作用。

图 3 TR3800 λ11/（λ011+2λs11）等值线图谱

图 4 TR3800 λ22/（λ022+2λs22）等值线图谱

图 5 TR3800 λ66/（λ066+2λs66）等值线图谱

本文在三体船操纵运动计算机数值仿真中，三体船的附加质量、附加惯性矩是按三维面元法计算的，包含有片体间的水动力干扰作用；而速度类导数是采用细长体理论结合切片法计算的，并据有关经验公式［10］进行了修正，暂未计入片体间的水动力干扰作用。研究表明，如此处理对三体船回转运动轨迹等仿真项目计算结果影响并不大。计算三体船速度类水动力导数的更好方法应该是计入龙格—库塔条件和尾涡面的三位面元法，作者及其所在课题组正在进行该项研究。

3 仿真计算实例

3.1 计算船型

取主、侧体均为方尾的某三体船型为计算船型（或称“目标”船型），该船型的主要几何参数如表2所示。

3.2 回转运动轨迹仿真

以目标船型TR3800为算例，联立求解式（11）～式（17），得该船在各种工况下的回转运动轨迹，图6～图13为TR3800三体船及其中体在18 kn、30 kn 两种航速和 10°、20°两种舵角下的回转运动轨迹，这种回转运动轨迹仿真图形可用于直观地分析、比较三体船回转运动特性。给出TR3800中体回转运动轨迹是为了将其与TR3800三体船回转运动轨迹对比，研究侧体对于回转运动的影响。需说明，三体船的中体较常规单体船细长，所以中体的回转特性还不能够代表常规单体船的回转特性。

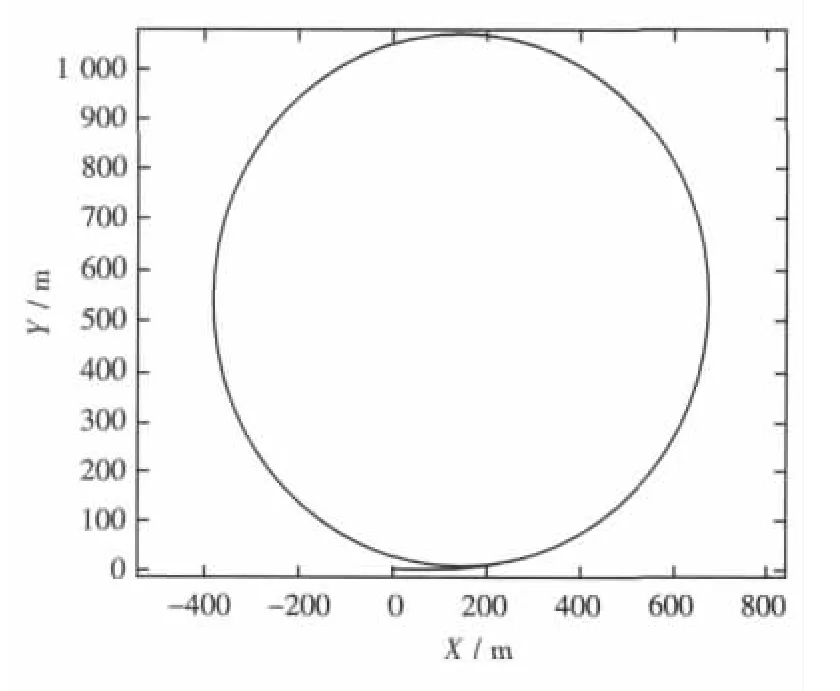
图6 TR3800船型主体10°、18 kn回转轨迹

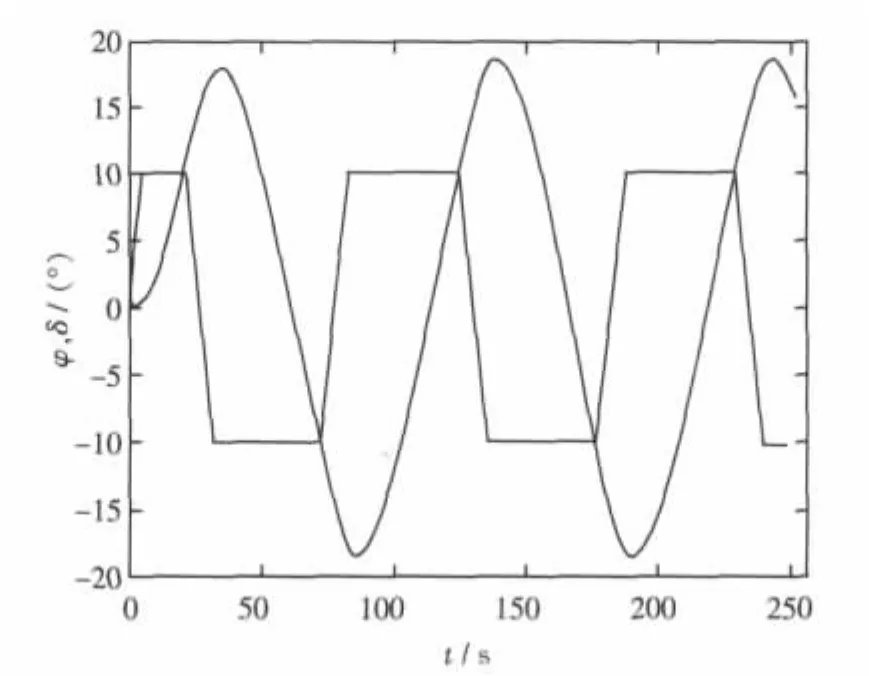
图7 TR3800船型主体35°、18 kn回转轨迹

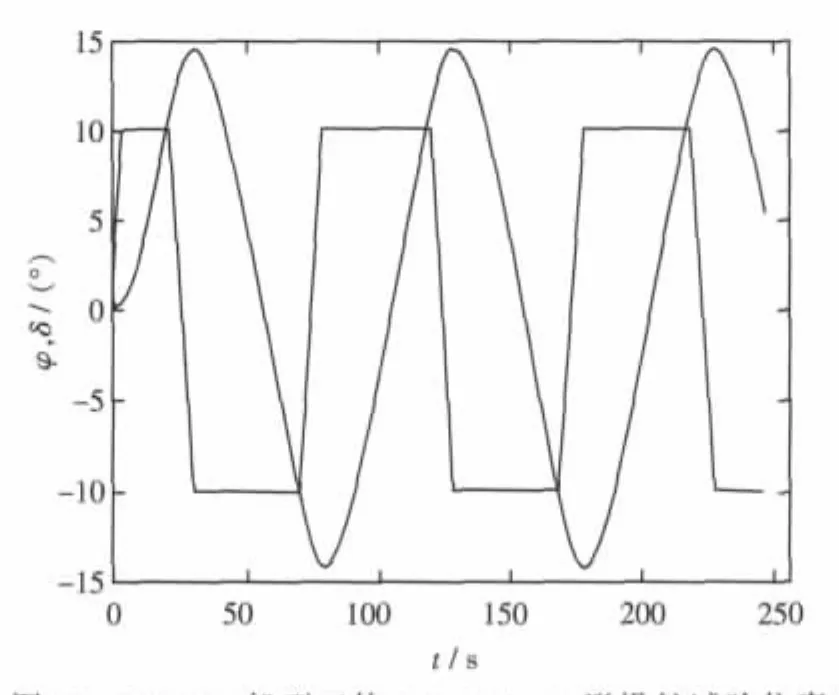
图8 TR3800船型三体10°、18 kn回转轨迹

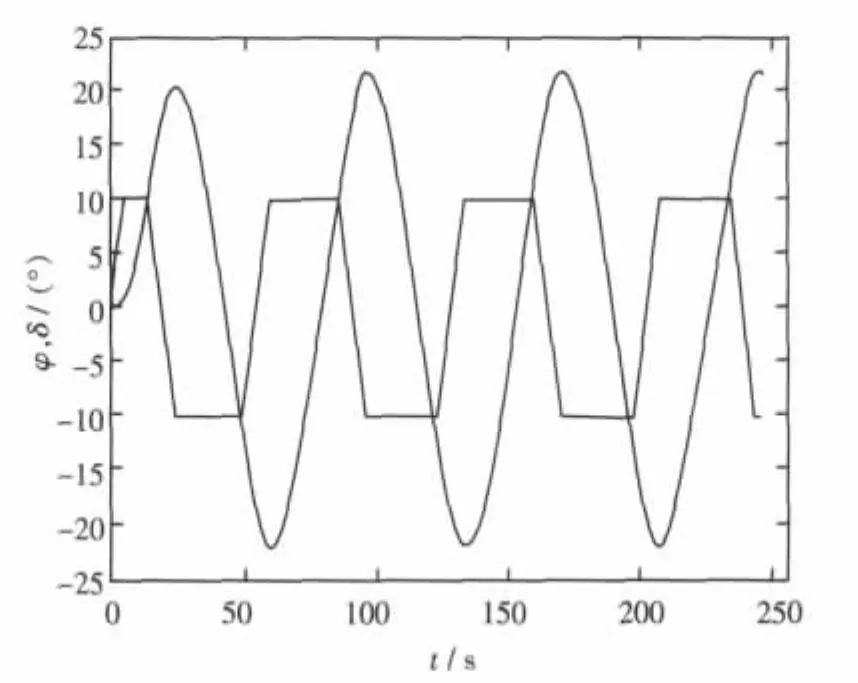
图9 TR3800船型三体35°、18 kn回转轨迹

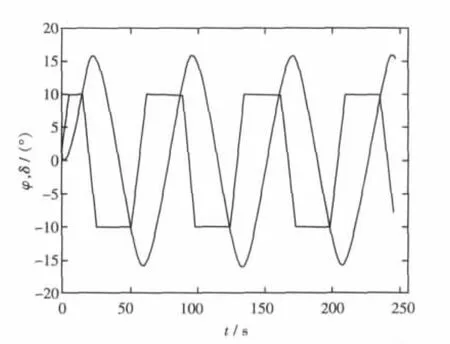
图10 TR3800船型主体10°、30 kn回转轨迹

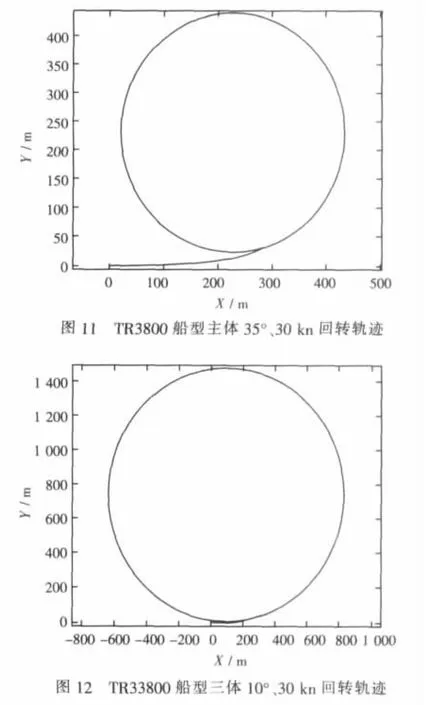
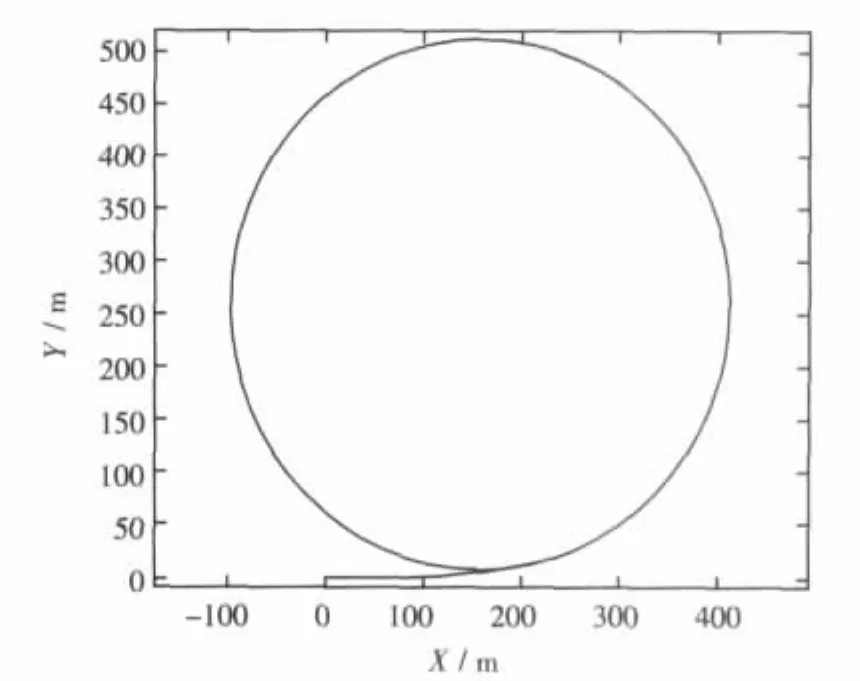
图13 TR3800船型三体35°、30 kn回转轨迹

3.3 Z型操纵试验曲线仿真

仍以目标船型TR3800为算例，按Z形操舵试验过程，联立求解式（11）～式（17）各式得该船Z形操舵试验曲线，如图14～图17所示。图中给出的是 18 kn、30 kn，10°／10°Z 形操舵试验仿真曲线。该曲线是评定对操舵响应的重要资料，由该图形可以测算出相应的φOV（超越角）、TL（转向滞后）、K、T等操纵性指标。

3.4 螺旋试验曲线仿真

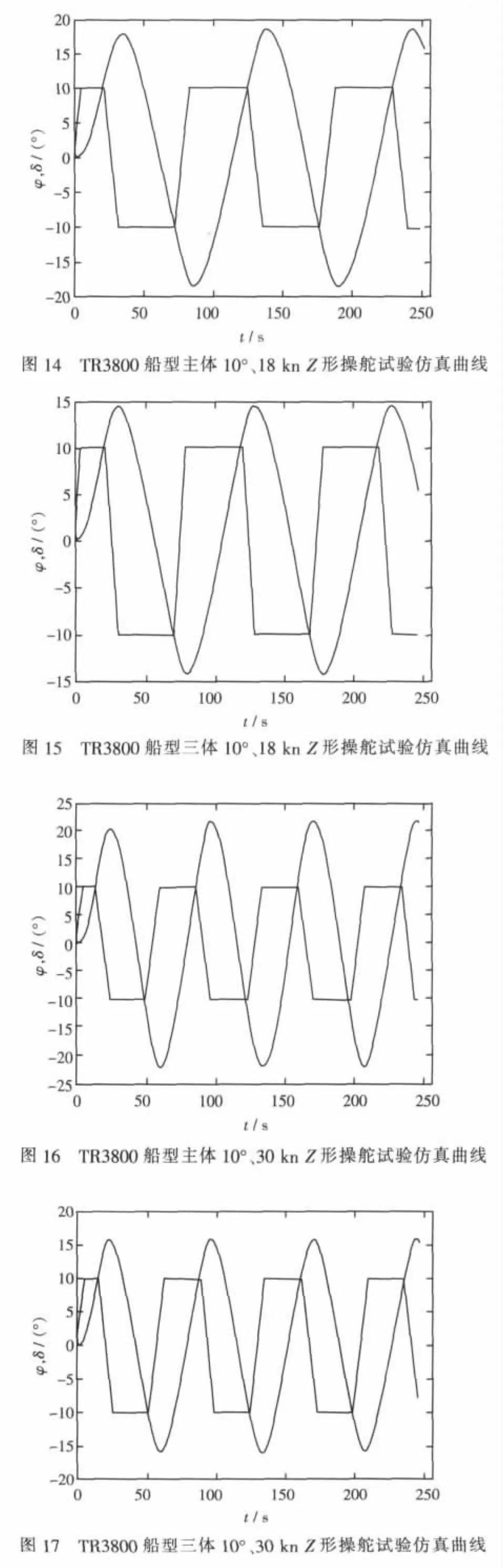
按式（8）、式（9）计算确定目标船型 TR3800主体和三体的18 kn螺旋试验仿真曲线。如图18、图19所示，可用于评估舰船的直线稳定性以及应舵性能。

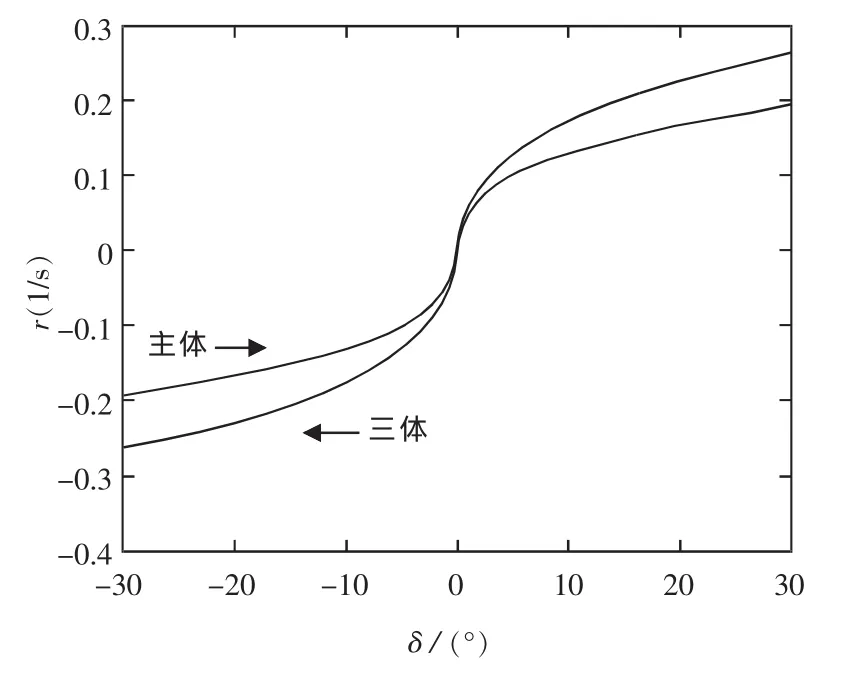
图18 TR3800船型18 kn操纵性曲线仿真图

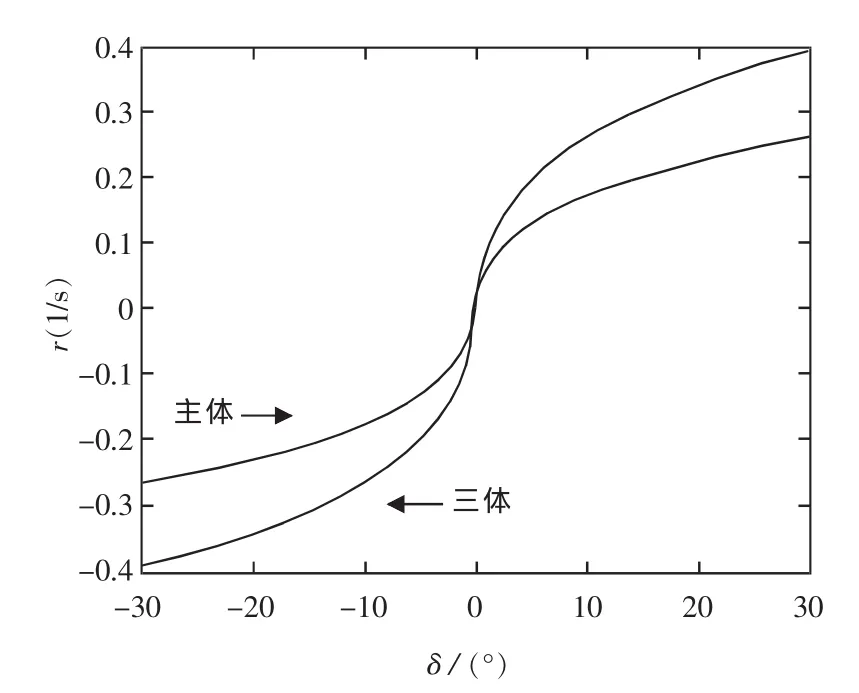
图19 TR3800船型18 kn操纵性曲线仿真图

4 三体船操纵特性分析

据目标三体船操纵特性计算机数值仿真结果为依据，结合船舶操纵性的一般概念和规律，对三体船操纵运动特性进行分析。

4.1 三体船操纵特性与“船舶操纵性标准”对比

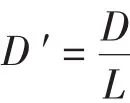
表3 船舶操纵性标准

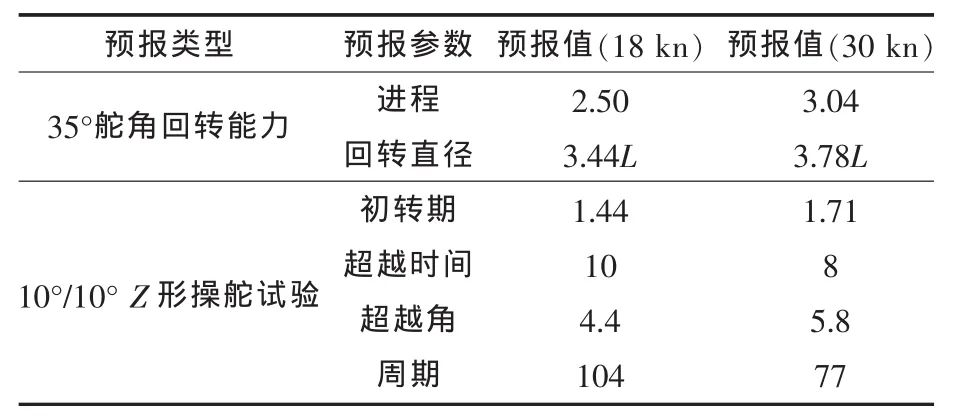
表4 TR3800预报值

4.2 三体船操纵特性分析

在18 kn航速、35°舵角下，对主体（作为单体船）与TR3800三体船操纵特性进行对比分析。二者计算机仿真所得回转运动轨迹如图20所示，表5给出了与图20相对应的更多操纵性指数仿真结果。由图20所示仿真计算轨迹可直观地看出三体船的定常回转特性较单体船略有下降，而三体船的初转特性较单体船好。轨迹仿真图形显示的结果与操纵性各项技术指标仿真结果反映的状况是一致的。

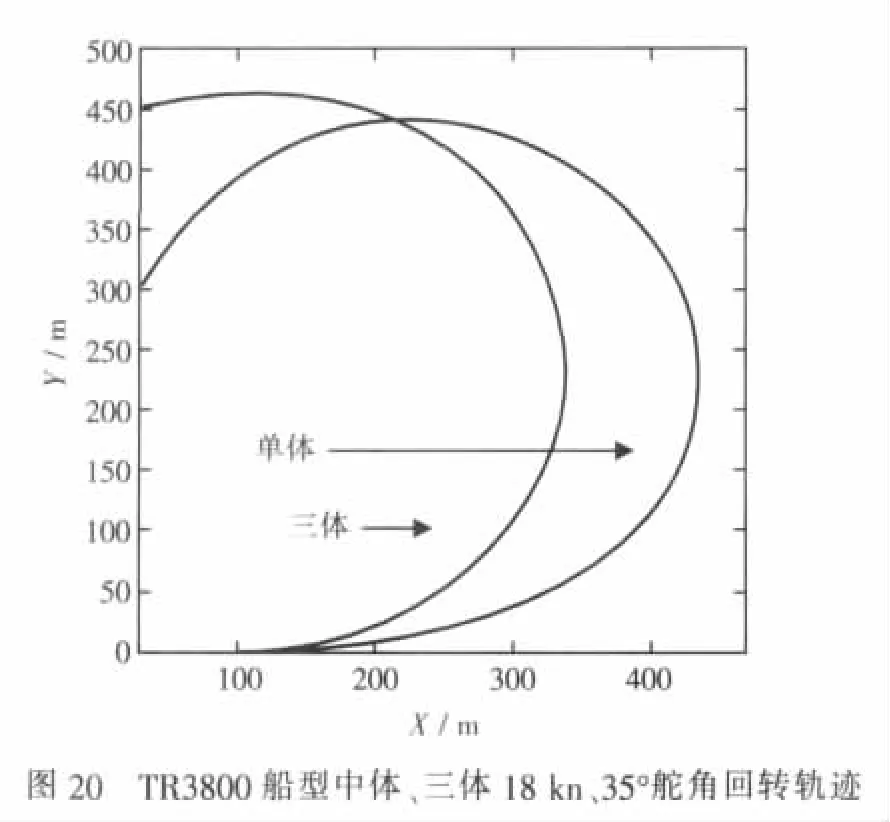
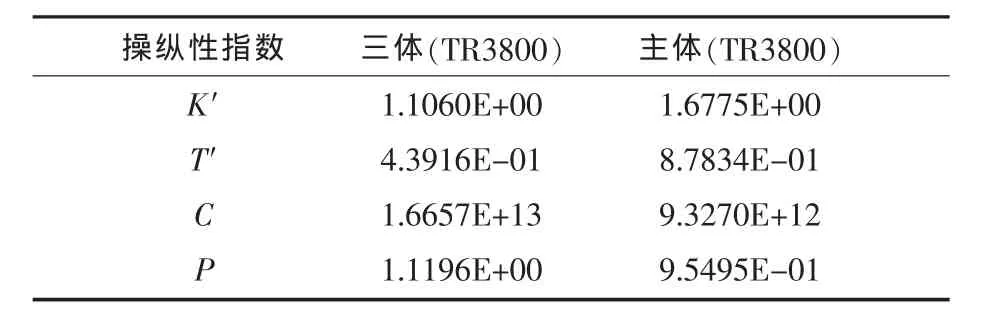
表5 TR3800操纵性指标预报值

据图20和表5对三体船操纵特性简要分析如下：

1）回转性。主体K′值大于相应三体，说明三体船的侧体受力状态不利于定常回转性能，这与本文得出的仿真图形显示的定性规律一致。三体船的回转性是以定常回转直径来衡量的，故得出初步结论是，三体船回转性较单体船有所下降。

2）航向稳定性。主体T′值明显大于三体船型，说明侧体受力状态有利于提高直线稳定性，这也与仿真图形显示的定性规律一致，故得初步结论为，三体船的直线稳定性能优于单体船。

3）三体船的跟从性和转首性与单体船相比有所提高。

5 结论

综上所述，可得如下结论：

1）仿真得出的三体船及其中体操纵特性图形和指数总体上合理，数值在正常范围内，本文三体船操纵特性仿真方法具有工程应用前景。

2）三体船定常回转特性较单体船有所下降，而直线稳定性却有所加强。

3）三体船的跟从性和转首性较单体船有所提高。

［1］ 卢晓平，郦云，董祖舜.高速三体船研究进展［J］.海军工程大学学报，2005（2）：43－48.

［2］ KANG K J，KIM SY，CHOIY R.Seakeeping and maneuvering performances of the 2500 tons class trimaran［C］//IWSH ’2001， Wuhan：Wuhan University of Technology Press，2001.

［3］ LUCA S，ROBERTA D，MICHELE V，et al.Design project of a trimaran multipurpose frigate—study of the hydrodynamic aspects ［C］//Proc.of the 7th International Conference on Fast Sea Transportation FAST 2003，Naples Italy，2003.

［4］ 卢晓平，姚迪，王波.三体船操纵性计算与特性分析［J］.海军工程大学学报，2009，21（1）：47-53.

［5］ 姚迪.三体船水动力导数计算与操纵特性仿真研究［D］.武汉：海军工程大学，2008.

［6］ 吴秀恒.船舶操纵性与耐波性［M］.北京：人民交通出版社，1999.

［7］ 贾欣乐，杨盐生.船舶运动数学模型［M］.大连：大连海事大学出版社，1999.

［8］ 卢晓平.舰船原理［M］.北京：国防工业出版社，2007.

［9］ 吴秀恒，刘祖源，施生达，等.船舶操纵性［M］.北京：国防工业出版社，2005.

［10］盛振邦，刘应中.船舶原理［M］.上海：上海交通大学出版社，2004.

Numerical Simulation of Maneuverability Characteristics of Trimaran

Lu Xiao－ping1 Yao Di2 Wang Zhong1
1 College of Naval Architecture and Power，Naval Univ ersity of Engineering，Wuhan 430033，China
2Military Representative Office in Dalian Ship building Industry Co.Ltd.， Dalian 116000，China

B ased on the theory ofmaneuverability differential equation of hydrodynamic form and K，T responsibility form（both linear and low degree nonlinear equation）， the article took the track motion differential equation of tr i maran gravity center as numerical si mulation foundation，themaneuverability feature of tr i maran including turning tracks，maneuverability curves and zigzagmaneuverability curves were calculated by means of Matlab si mulation software，the calculation results were compared with that of monohull.T he caculated results are reasonable and show that the characteristics of constant turning of the trimaran is less than that ofmonohull， and beeline stability respectively enhanced， follow-up steering and course changing quality improved.

Hess－Smithmethod； slender hull theory； stripmethod； maneuverability； trimaran

U674.951

A

1673－3185（2010）03－01－07

10.3969/j.issn.1673-3185.2010.03.001

2010-01-19

海洋工程国家重点实验室基金项目（0706）

卢晓平（1957－），男，教授，博士生导师。研究方向：船舶流体力学。E-mail：luxiaoping100@163.com