非线性色散方程的初边值问题

陆博，李巧萍，杨素敏

（河南科技学院，河南新乡453003）

对于杆中非线性波的传播问题,国内外学者从不同的角度进行了许多重要的研究.初等理论给出的经典的弹性杆的波动方程是线性的,非色散的,为了改善初等理论的结果，文献［1］基于能量的考虑,导出了计算横向惯性的杆的运动方程.实际上,当压缩波沿纵向传播时,由于Possion效应,将会伴随有横向运动,横向运动不仅对杆的动能有贡献,而且由于波剖面的不均匀性会产生横向剪切,从而对应变能也有贡献.文献［1］同时考虑这两种横向效应产生的几何色散,并由三次非线性本构关系产生的物理非线性,借助Hamilton变分原理导出了弹性杆的非线性纵向四阶非线性波动方程.由于此方程是描述着在具有色散效应的介质中波的传播的非线性方程.因此粘性的修正效应如何是此类问题所需回答的基本问题之一,故研究具有粘性阻尼项的非线性波动方程是有意义的.文献［2］研究了带有阻尼项的广义立方双色散方程解得存在性,唯一性和解的衰减性质，并给出解不存在的充分条件.本文应用Galerkin方法和Sobolev空间及紧性原理研究一类波动方程的初边值问题的整体广义解和整体古典解的存在性和惟一性.

1 整体解的存在惟一性

考虑初边值问题（1）～（3）

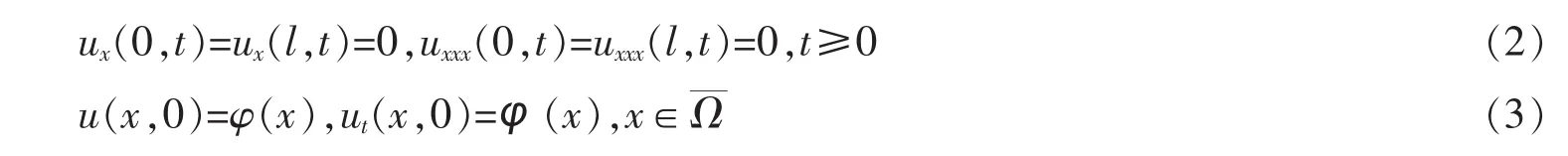
其中 a>0，b>0 为常数，u（x，t）是未知数,下标 x 和 t分别表示对 x 和 t求偏导数，f（s）表示给定的非线性函数 φ（x）和 φ（x）是定义在 Ω=（0，l）和上的已知函数.

令｛y，（x）｝是由如下常微分方程的特征值问题

对应于特征值 λ（i=1，2，……）的特征函数构成的 L2［0，1］空间的一标准正交基，其中’=.

设问题（1）～（3）的 Galerkin 近似解为

其中 αNi（t）是待定系数，N 为自然数，假设初值函数 φ（x）和 φ（x）可表示为

其中 μi和 vi（i=1，2，…） 是常数.将近似解 uN（x，t）代入方程（1），两边同乘以 ys（x）并在[0，l]上积分，可得如下方程

其中（·，·）为空间 L2［0，1］的内积.

将近似解 uN（x，t）和初值函数的近似代入方程（1）和初值条件（3）可得

为了证明初边值问题（1）～（3）整体广义解的存在性，下面对近似解作一系列估计.

引理 1 设 f∈C1（R），C0为常数，使得对任意的 s∈R，成立 f ′（s）≥C0，φ∈H2（Ω），φ∈H1（Ω），且 φ（x）和 φ（x）满足边界条件（2），则对任意的 N，初值问题（5），（6）有整体古典解 αNs∈C2［0，T］（s=1，2，…），且有下面的估计

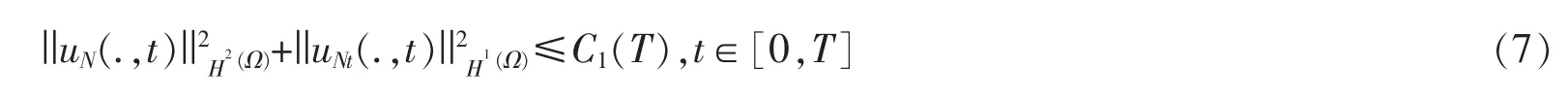
其中常数 C1（T）及 Ci（T）是仅依赖于（i=2，3，…）的常数，‖·‖表示 L2（Ω）空间的范数.证明令 f0（s）=f（s）-δs-f（0），δ=min｛C0，0｝（≤0），则 f0（0）=f0′（s）=f0′（s）-δ≥0

因此 f0（S）是单调增函数，故

则式（1）转化为下面的等式

于是式（5）与下面的方程组等价于

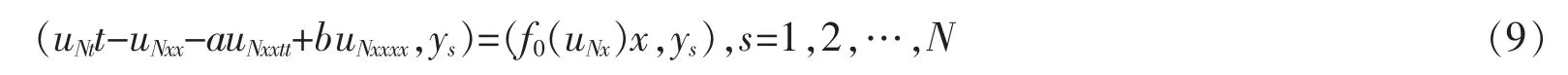
在式（9）两端同时乘以 2αNst（t），对 s=1，2，…，N 求和，在等式两端同时加生上 2（uN，uNt），对 x 分部积分和利用Gronwall不等式推出

应用文献［3］的方法，利用式（10）和Leray-Shauder不动点原理可以证明初值问题式（5）,式（6）存在解.

aNs∈C2［0，T］，s=1，2…，N.定理得证.

进一步利用Gronwall不等式和弱紧性原理可以证明

引理 2 假设引理 1 的条件成立，若 f∈C3（R），φ∈H5（Ω），φ∈H4（Ω），则问题（5），（6）的近似解满足下列估计:

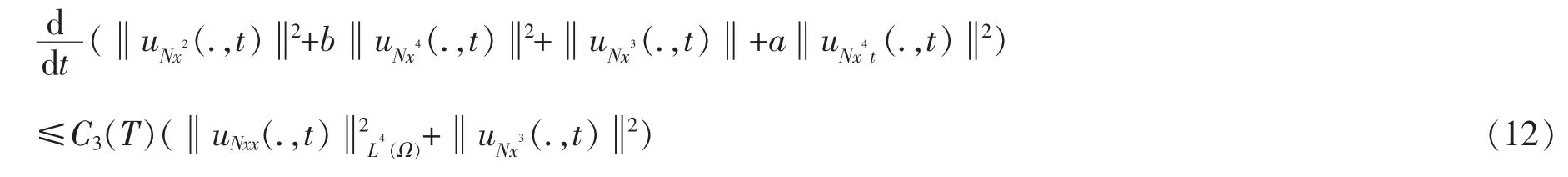
利用Gagliardo-Nirenberg插值定理[4-5],Young不等式和Gronwall不等式,可以得到

式（5）两端同乘以-2aNstt（t），对 s=1，2，…，N 求和，对 t分部积分,利用 Sobolev 嵌入式（7）和式（13），得到

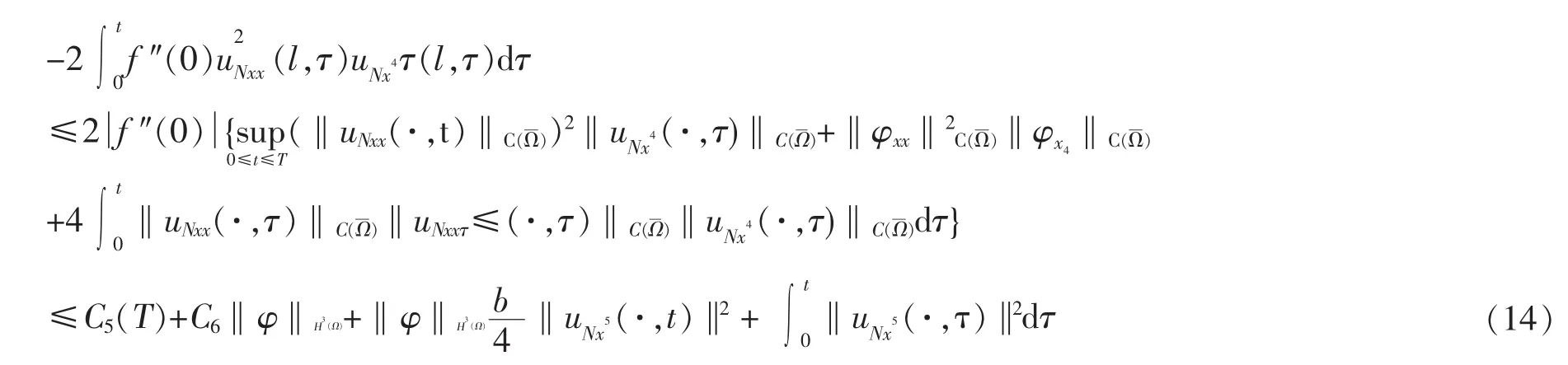
类似于式(14)，可以证明得

利用 Sobolev嵌入定理,式(7)和式(13),于是

把式(14)-(16)带入到式(13)中，利用Gronwall不等式，得到

式（5）两端同乘以 αNstt（t）+αNstt（t）对 s=1，2，…，N，求和,并利用 Cauchy 不等式及估计式（7）与式（17）和Sobolev嵌入定理推出

定理得证.

定理 1在引理2的条件下,则初边值问题式（1）～（3）存在惟一的整体广义解

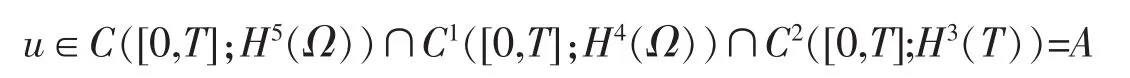
证明:从不等式（11）,利用Sobolev嵌入定理和弱紧性原理,式（1）～（3）存在整体广义解,这个解是惟一存在的，定理得证.

下面考虑问题式（1）～（3）的整体古典解的存在性.

利用文献[6]可证明下述引理，

引理 3 假设引理 2 的条件成立.如果 φ∈H7（Ω）和，φ∈H6（Ω），f∈C4（R）和 f（i）（0）=0（i=2，4）.则问题式（1）～（3）的近似解满足下列估计

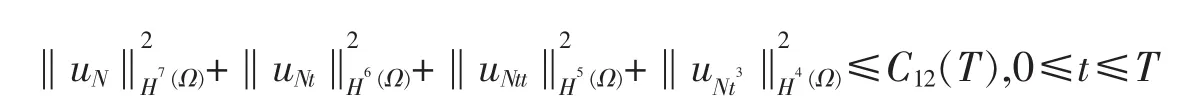
利用引理3和采用定理1证明步骤,可以证明定理 2在引理3的条件下，问题式（1）～（3）有惟一的广义古典解

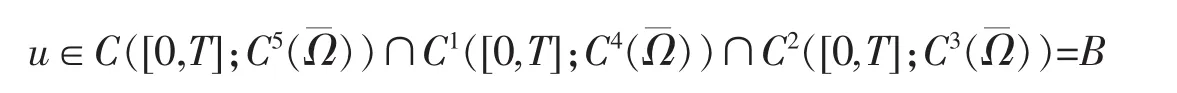
2 结论

针对一类非线性纵向波动方程的初边值问题，应用Galerkin方法、Leray-Shauder不动点原理、Gagliardo-Nirenberg插值定理和Gronwall不等式对方程的对近似解作初步估计，并借助Sobolev嵌入定理和弱紧性原理逐步提高其光滑性，对近似解估计进行细化.在此基础上，先后解决了此类非线性方程整体广义解和整体古典解的存在性和惟一性问题.给出了存在惟一性定理：定理1和定理2，即在初值足够光滑的条件下，四阶非线性波动方程的初边值问题式(1)～(3)存在惟一的整体广义解和整体古典解.

所得结果为研究此问题的解的正则性、解的渐进性和解的爆破等其他性质提供了条件，同时也为解决方程的精确解问题提供了理论基础.

[1]刘志芳，张善元.圆杆波导中的一个非线性波动方程及准确周期解［J］.物理学报，2006，14（2）:628-632.

[2]Chen G，Wang Y，Wang S.Initial boundary value problem of the generalized cubic double dispersion equation ［J］.J Math Anal Appl，2004，299（11）：563-577.

[3]Chen G，Xing J，Yang Z.Cauchy problem for generalized IMBq equation with several variables［J］.Nonlinear Anal， 1996，26（2）:1255-1270.

[4]Robert A Adams.Sobolev Spaces［M］.New York:Academic Press，2003.

[5]Vladimir G Mazja.Sobolev Spaces［M］.New York:Springer-Verlag，1985.

[6]Chen G，Lu B.The initial-boundary value problems for a class of nonlinear wave equations with damping term ［J］.J Math Anal Appl，2009，351（3）：1-15.