开关变换器双频率控制技术
王金平, 许建平, 兰燕妮
(西南交通大学电气工程学院,四川 成都 610031)
0 引言
开关变换器因其具有高功率转换效率和高功率密度等明显优点而逐步取代传统线性稳压电源,得到了越来越广泛的应用。目前,开关变换器控制普遍采用脉冲宽度调制(pulse width modulation,PWM)技术[1]。PWM通过对脉冲宽度的连续调整实现对输出电压的控制,它是一种线性控制。开关变换器本质上属于强非线性系统[2-3],基于线性反馈控制的PWM变换器很难获得令人满意的动态响应特性和控制系统鲁棒性,因而有必要研究开关变换器的非线性控制技术。近年来,越来越多的非线性控制技术在开关变换器控制系统中得到了重视和应用[4-12]。
本文提出了一种开关变换器非线性控制技术——双频率(bi-frequency,BF)控制技术。根据输出电压与参考电压大小的比较结果,BF控制器采用高频率脉冲或低频率脉冲对开关变换器进行控制,从而实现开关变换器输出电压的调节,以维持输出电压的稳定。BF控制实现简单,无需误差放大器及其繁琐的补偿网络设计,具有优异的动态响应特性和鲁棒性。文中对比研究了两种BF控制技术:电压型双频率(voltage-mode bi-frequency,VM-BF)控制和电流型双频率(current-mode bi-frequency,CM-BF)控制,分析了它们的工作过程、特性和控制规律。理论分析、仿真及实验结果表明,CM-BF具有更为优越的控制性能。
1 开关变换器双频率控制
1.1 双频率控制原理
双频率控制采用两组具有不同开关频率的控制脉冲对开关变换器进行控制。图1所示为BF控制开关变换器结构框图。

图1 双频率控制结构框图Fig.1 Block diagram of BF control
当采样/保持器采样时钟clk来临时,BF控制器采样输出电压Vo,若采样的输出电压小于参考电压Vref,则比较器的输出结果对选择器进行控制,选择工作频率为fH的高频率脉冲PH作为控制脉冲,以提升输出电压;反之,若采样的输出电压大于参考电压Vref,则比较器的输出结果对选择器进行控制,选择工作频率为fL(fH=kfL,k>1)的低频率脉冲PL作为控制脉冲,以降低输出电压。稳态工作时,若干个高、低频率脉冲构成一个脉冲序列,BF控制开关变换器以此脉冲序列进行循环,将该脉冲序列持续的时间称之为脉冲序列循环周期。BF控制器通过改变脉冲序列循环周期内高、低频率脉冲的组合,实现开关变换器输出电压的控制。
1.2 VM-BF和CM-BF控制
根据控制结构实现方式的不同,BF控制技术可以分为如图2所示的VM-BF控制和CM-BF控制。
图2(a)中,VM-BF控制器仅由输出电压外环构成,高、低频率脉冲PH和PL由脉冲产生器产生,采样时刻输出电压Vo与参考电压Vref间的大小关系作为选择控制脉冲PH或PL的依据。当输出电压小于参考电压时,高频率脉冲产生器工作,控制器选择PH作为控制脉冲;反之,控制器选择PL作为控制脉冲。在VM-BF中,PH和PL具有相同的导通时间,不同的开关频率。
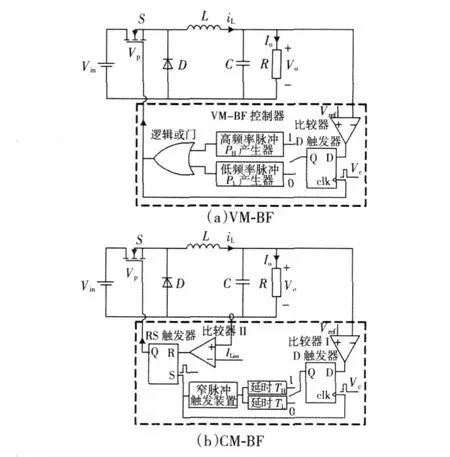
图2 VM-BF和CM-BF控制电路图Fig.2 Circuit diagram of VM-BF and CM-BF control
图2(b)中,CM-BF控制器由输出电压外环和电感电流内环组成,此时高、低频率脉冲不再由脉冲产生器产生,而是由输出电压外环与电感电流内环共同生成,输出电压外环决定当前控制脉冲周期为TH(1/fH)或TL(1/fL),电感电流内环决定当前控制脉冲的关断时刻,而开通时刻为当前控制脉冲的开始时刻。
图3(a)、3(b)分别示出了VM-BF和CM-BF控制DCM Buck变换器的主要工作波形,下面分析它们的工作过程及控制策略。
对于如图3(a)所示VM-BF控制,在任意控制脉冲周期开始时刻,触发脉冲Vc有效,D触发器被触发,其Q端电平与D端保持一致;当Q为低电平时,表明控制脉冲周期开始时刻的输出电压高于参考电压,VM-BF控制器选用低频率脉冲PL作为当前开关周期的控制脉冲,以降低输出电压;反之,当Q为高电平时,表明输出电压低于参考电压,控制器将选择高频率脉冲PH作为当前开关周期的控制脉冲,以提升输出电压。
对于如图3(b)所示CM-BF控制,在任意控制脉冲周期开始时刻,触发脉冲Vc有效,RS触发器置位,开关管S导通,电感电流线性上升;同时,D触发器被触发,其输出端电平状态与D端保持一致,当输出端为高电平时,表明控制脉冲周期开始时刻输出电压低于参考电压,此时控制器选择TH作为当前控制脉冲的工作周期;反之,表明输出电压高于参考电压,控制器将选择TL作为当前控制脉冲的工作周期;控制器在经过TH或TL时间后,触发脉冲Vc再次有效,进入下一开关周期。在任意控制脉冲周期内,当电感电流线性上升到电流限定值ILim时,开关管关断。
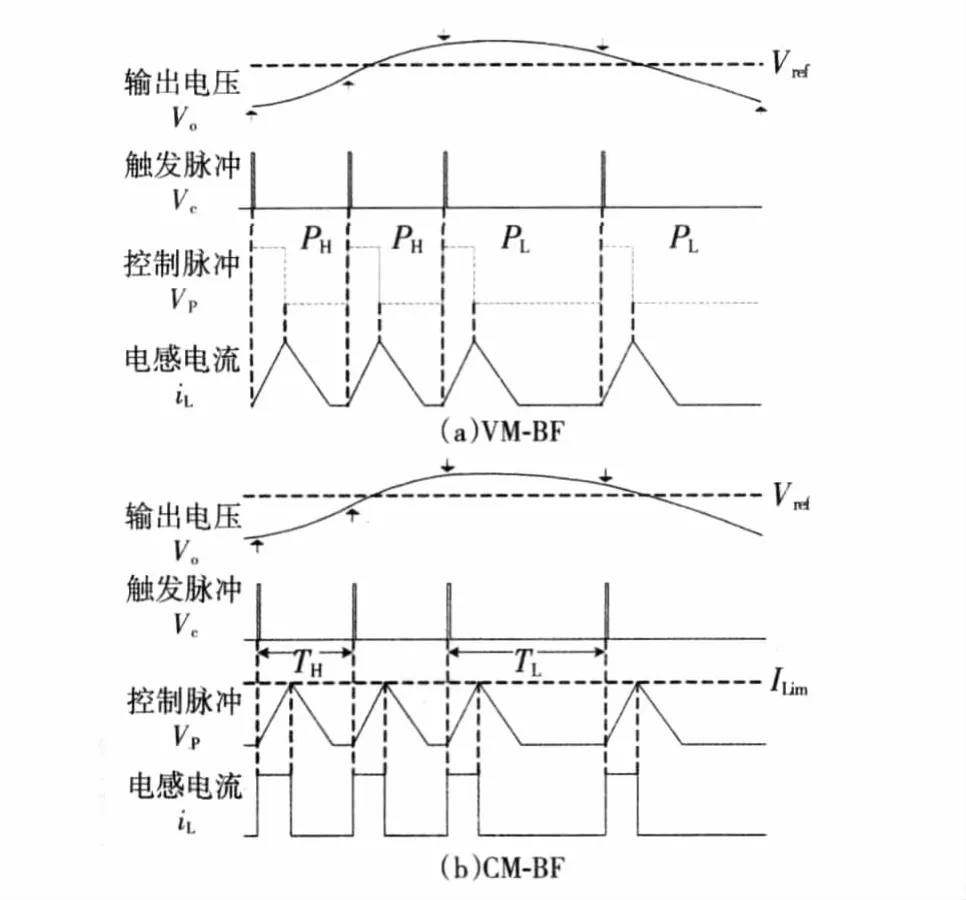
图3 VM-BF和CM-BF控制DCM Buck变换器波形Fig.3 Operation waveforms of VM-BF and CM-BF controlled DCM buck converter
对于 VM-BF和CM-BF控制 DCM Buck变换器,当采用高频率脉冲工作时,变换器可以向负载端传递更多的能量。因而,VM-BF和CM-BF控制器均可以通过改变高、低频率脉冲序列的组合形式,使输入和输出能量在脉冲序列循环周期内达到动态平衡,以维持输出恒定。
1.3 VM-BF和CM-BF的特点
从图2可以看出,VM-BF控制原理简单,控制器仅由比较器及一些简单的逻辑器件组成,控制环仅由输出电压环构成,不需要对开关变换器的其它状态变量进行检测及处理,易于实现。此外,不同于开关变换器的PWM控制方式,VM-BF用比较器取代误差放大器,仅需检测控制脉冲周期开始时刻输出电压与参考电压间的大小关系,以采用相应的控制脉冲对变换器进行调整,因而具有快速的负载动态响应速度和优异的鲁棒性。
CM-BF在VM-BF基础上将电感电流引入到控制环路中,从而提升了开关变换器输入电压动态响应速度,具有自动限流功能,易于实现过流保护及多台变换器间均流,而且在启动过程中不会出现输出电压及电感电流过冲现象。
2 BF控制DCM Buck变换器
2.1 VM-BF控制DCM Buck变换器分析
假定VM-BF控制的高、低频率脉冲PH和PL的周期分别为TH和TL,占空比分别为DH和DL,则当VM-BF控制DCM Buck变换器分别采用PH和PL工作时,输入电流平均值分别为
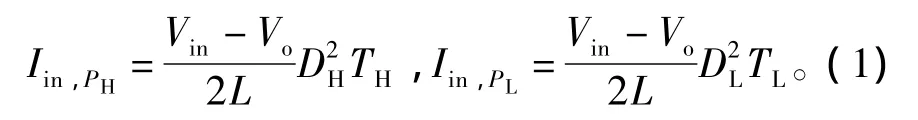
因此,输入端提供的能量分别为
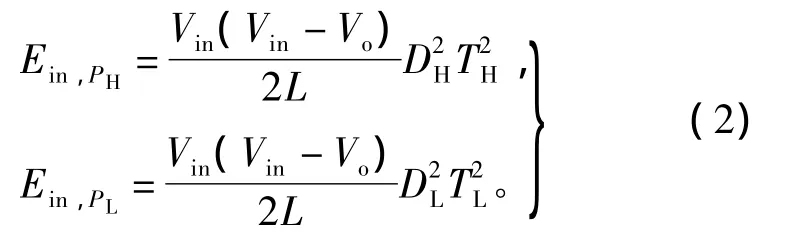
在稳态工作时,假定一个脉冲序列循环周期T由μH个高频率脉冲PH与μL个低频率脉冲PL组成,由此可得到VM-BF控制DCM Buck变换器平均输入功率

若变换器转换效率为η,将式(2)代入式(3)可得输出功率

式(4)揭示了VM-BF控制DCM Buck变换器的输出功率、输入电压和输出电压、转换效率、电感值、PH和PL占空比、周期以及脉冲序列循环周期内PH和PL个数之间的定量关系。
由式(4)可以进一步得到脉冲序列循环周期内高频率脉冲PH和低频率脉冲PL的比例关系为

由式(5)可以看出,随着输出功率的增加,比值μH/μL增加,表明脉冲序列循环周期内高频率脉冲PH增加,VM-BF控制器通过选用更多的高频率脉冲工作,以向负载端传递更多的能量。
2.2 CM-BF控制DCM Buck变换器分析
与VM-BF控制不同,CM-BF的控制脉冲的导通时间由电感电流决定。由图3(b)可得控制脉冲Vp的导通时间为

由此可以得到CM-BF控制DCM Buck变换器在控制脉冲周期TH和TL内,输入电流平均值分别为
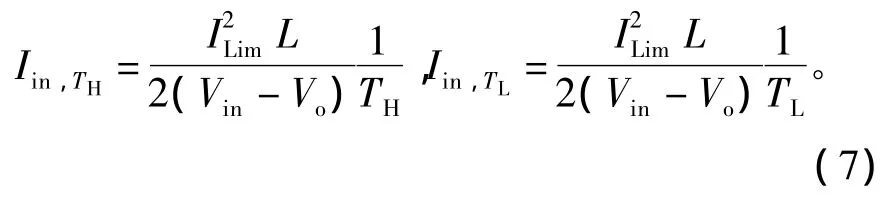
因此,输入端提供的能量为

借鉴式(3)、式(4),可得 CM-BF控制 DCM Buck变换器输出功率

式(9)揭示了CM-BF控制DCM Buck变换器的输出功率、输入电压和输出电压、转换效率、电感值、电流限定值ILim、以及脉冲序列循环周期内PH和PL个数之间的定量关系,在进行控制系统设计时作为参考。
同样对式(9)进行变换,可得脉冲序列循环周期内PH和PL个数的比例关系为
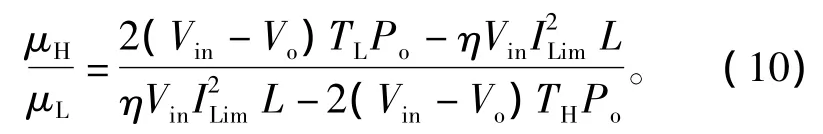
由式(10)可以看出,当输出功率越大时,μH/μL比值越大,表明脉冲序列循环周期内高频率脉冲数目也越多,这一特性与VM-BF控制类似。
3 仿真研究
为了验证VM-BF控制和CM-BF控制的性能,采用PSIM软件进行了电路仿真研究。为便于对比分析,选择恰当的控制参数,使得VM-BF控制和CM-BF控制DCM Buck变换器具有相同的稳态结果。主要仿真参数如下:Vin=14 V,Vo=Vref=6 V,L=5 μH,C=470μF,TH=5 μs,TL=20 μs;VM-BF控制的DH=0.4、DL=0.1,CM-BF控制的电流限定值ILim=3.2 A。
图4为VM-BF控制和CM-BF控制DCM Buck变换器启动时的输出电压及电感电流波形。变换器启动工作时,输出电压很低,电感电流上升斜率很大。在输出电压上升到参考电压以前,控制器均采用高频率脉冲工作。对于VM-BF控制,控制脉冲占空比固定为DH,因而电感电流快速上升,过冲严重,造成输出电压超调。因此,VM-BF控制时,往往需要额外设计软启动电路或过流保护电路;而对于CM-BF控制,由于电感电流峰值受限,因而启动时控制脉冲占空比受限,从而使得变换器具有平滑的启动过程,无过冲现象和输出电压超调。

图4 VM-BF和CM-BF控制DCM Buck变换器启动过程特性Fig.4 Start-up process of VM-BF and CM-BF controlled buck converter
图5所示为不同输出功率时,BF控制DCMBuck变换器的稳态仿真结果,其中电路参数选取使得VMBF控制和CM-BF控制具有相同稳态结果。
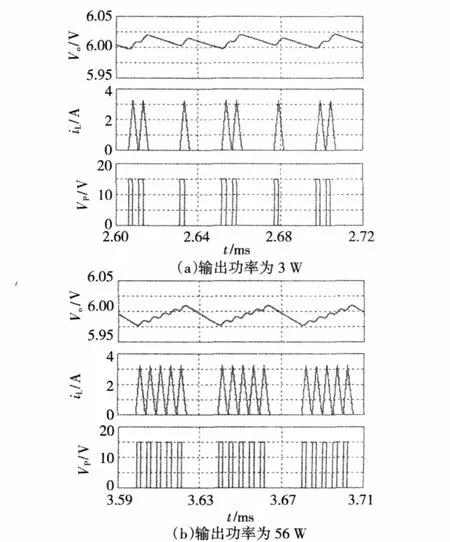
图5 BF控制DCM Buck变换器稳态仿真结果Fig.5 Steady-state simulation results of BF controlled buck converter
从图5(a)可以看出,当输出功率为3 W时,脉冲序列循环周期由1PH-2PL组成,此时μH/μL=0.5,这与由式(5)和式(10)得到的理论结果一致;在图5(b)中,当输出功率为5.6 W时,脉冲序列循环周由 4PH-1PL组成,此时 μH/μL=4,同样与式(5)、式(10)所得结果相符。此外,对比图5(a)、5(b)可以看出,随着输出功率的增加,BF控制器将采用更多的高频率脉冲PH工作,以满足负载要求,与理论分析相符。从图5可以看出,5.6 W时输出电压低于3 W时输出电压,这是因为BF控制Buck变换器的高、低频率脉冲是针对特定的负载而设计的,而当负载功率小于/大于特定负载功率时,输出电压平均值将略高于/低于期望输出电压。
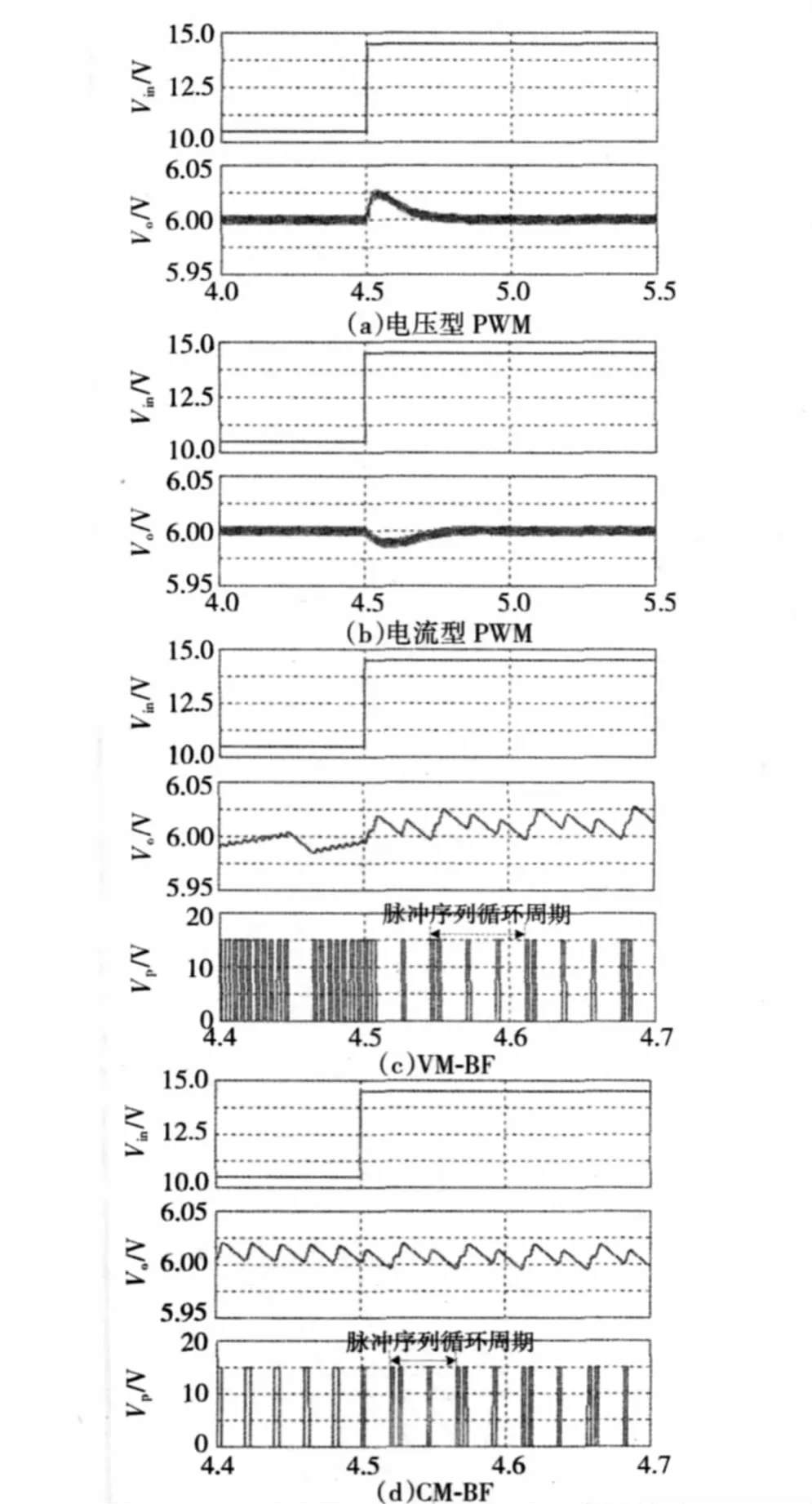
图6 采用不同控制方法时DCM Buck变换器的输入电压动态响应对比Fig.6 Comparison of input voltage dynamic response of DCM buck converter under different control method
图6为当输入电压由10.5 V突变至14.5 V时,采用不同控制方法的DCM Buck变换器的输入电压动态响应特性,其中电压型PWM与电流型PWM控制的开关周期均为10 μs。由图6可以看出,当输入电压突变时,VM-BF控制和CM-BF控制具有比传统电压型PWM与电流型PWM更好的输入电压动态响应性能。在图6(c)、6(d)中,输入电压突变前后,VM-BF控制和CM-BF控制DCM Buck变换器的稳态结果不一致,这是由于输入电压值不是额定输入电压14 V的缘故。从图6(c)可以看出,随着输入电压增加,控制脉冲中高频率脉冲数明显减少,当输入电压突变后,新的脉冲序列循环周期为1PH-3PL;在图6(d)中,随着输入电压增加,控制脉冲占空比变小,控制脉冲中高频率脉冲数增加,这与VM-BF控制不同;此外,从图6(d)还可以看出,当输入电压突变后,稳态时的脉冲序列循环周期为1PH-2PL。对比图6(c)和6(d)可以看出,输入电压突变后,VM-BF控制调整时间为一个高频率脉冲周期和两个低频率脉冲周期,而CM-BF仅经过一个低频率脉冲周期的时间完成输出电压的调整。由此可知,CM-BF具有更快的输入电压动态响应速度。
4 实验验证
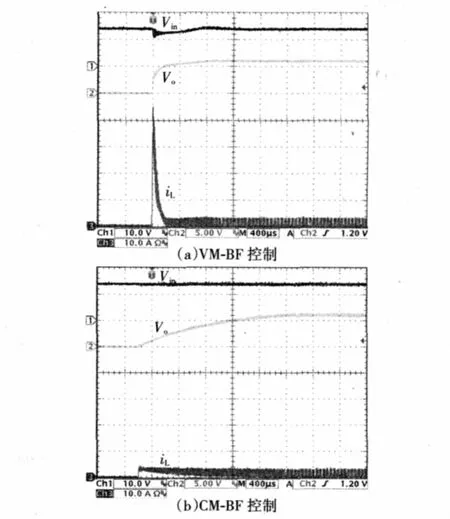
图7 VM-BF控制和CM-BF控制DCM Buck变换器启动实验结果Fig.7 Experimental results of start-up process of VM-BF and CM-BF controlled buck converter
为了验证理论分析及仿真结果的正确性,采用与仿真一致的电路参数搭建实验系统。图7给出了出了VM-BF控制和CM-BF控制DCM Buck变换器启动时的实验结果。从图7(a)可以看出,对于VMBF控制Buck变换器,启动瞬间电感电流较大,引起输入电压Vin跌落,从而实验结果与仿真有一定区别;而从图7(b)可以看出,对于CM-BF控制Buck变换器,由于电感电流限定值ILim的存在,使得变换器具有平滑的启动过程,无输出电压及电感电流过冲,易于保护开关器件。
图8为VM-BF控制和CM-BF控制DCM Buck变换器在不同输出功率时的稳态实验结果。从图中可以看出,随着输出功率的增加,脉冲序列循环周期内高频率脉冲数增加,以向负载端传递更多的能量,这与理论分析相符。对比图5和图8可以看出,仿真和实验结果中脉冲序列循环周期内高、低频率脉冲的组合形式有一定差别,这是由实验电路中变换器转换效率不为100%造成的。
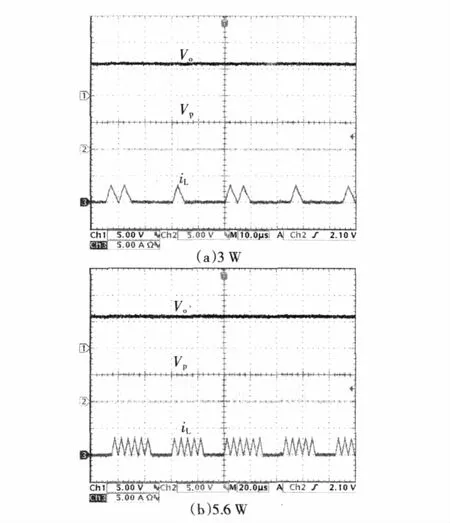
图8 VM-BF控制和CM-BF控制DCM Buck变换器稳态实验结果Fig.8 Steady-state experimental results of VM-BF and CM-BF controlled buck converter
5 结论
本文提出并研究了开关变换器双频率控制技术,分析了双频率控制电压型及电流型两种实现方式的工作特性及控制规律。文中对VM-BF控制和CM-BF控制DCM Buck变换器进行了深入研究,推导了变换器主电路参数与控制参数之间的定量关系,并得出了循环周期内高、低频率脉冲数量的比值关系。文中从启动特性、稳态特性以及输入电压动态响应特性三个方面对VM-BF控制和CM-BF控制进行了对比研究,结果表明CM-BF控制具有更为优越的控制性能,验证了理论分析的正确性。
[1]张占松,蔡宣三.开关电源的原理与设计[M].北京:电子工业出版社,1998:1-15.
[2]许峰,徐殿国,柳玉秀.具有最优动态响应的PWM型DC-DC变换器非线性控制新策略[J].中国电机工程学报,2003,23(12):133-139.XU Feng,XU Dianguo,LIU Yuxiu.A novel nonlinear control method for PWM DC-DC converter with optimizing transient response[J].Proceedings of the CSEE,2003,23(12):133-139.
[3]张波.电力电子变换器非线性混沌现象及其应用研究[J].电工技术学报,2005,20(12):1-6.ZHANG Bo.Study of nonlinear chaotic phenomena of power converters and their applications[J].Transactions of China Electrotechnical Society,2005,20(12):1-6.
[4]SMEDLEY K M,C'UK S.One-cycle control of switching converters[J].IEEE Transactions on Power Electronics,1995,10(6):625-633.
[5]CASTILLA M,VICUNA L G de,GUERRERO J M,et al.Designing VRM hysteretic controllers for optimal transient response[J].IEEE Transactions on Industrial Electronics,2007,54(3):1726-1738.
[6]CASTILLA M,VICUNA L G de,GUERRERO J M,et al.Simple low-cost hysteretic controller for single-phase synchronous buck converters[J].IEEE Transactions on Power Electronics,2007,22(4):1232-1241.
[7]TAN S C,LAI Y M,TSE C K.General design issues of sliding mode controllers in DC-DC converters[J].IEEE Transactions on Industrial Electronics,2008,55(3):1160 -1174.
[8]倪雨,许建平.一种离散全局滑模控制Buck变换器设计[J].电机与控制学报,2009,13(1):112-116.NI Yu,XU Jianping.Design of a novel discrete global sliding mode controlled Buck converter[J].Electric Machines and Control,2009,13(1):112 -116.
[9]张黎,丘水生.Buck变换器的积分重构滑模控制[J].电机与控制学报,2006,10(1):93-96.ZHANG Li,QIU Shuisheng.Integral reconstructors sliding mode control for Buck converter[J].Electric Machines and Control,2006,10(1):93-96.
[10]TELEFUS M,SHTEYNBURG A,FERDOWSI M,et al.Pulse trainTM,a novel digital control method,applied to a discontinuous mode flyback converter[C]//IEEE 34th Annual Power Electronics Specialist Conference,June 15 -19,2003,Acapulco,Mexico.2003:1141-1146.
[11]FERDOWSI M,EMADI A,TELEFUS M,et al.Pulse regulation control technique for flyback converter[J].IEEE Transactions on Power Electronics,2005,20(4):798 -805.
[12]秦明,许建平,王金平,等.多级脉冲序列控制Boost变换器[J].电机与控制学报,2009,13(4):533-540.QIN Ming,XU Jianping,WANG Jinping,et al.Multilevel pulse train controlled Boost converter[J].Electric Machines and Control,2009,13(4):533-540.

