SVPWM过调制中控制角算法的分析与应用

王旭东， 张思艳， 余腾伟

(哈尔滨理工大学电气与电子工程学院，黑龙江哈尔滨150080)

0 引言

空间矢量脉宽调制(SVPWM)技术，由于具有简便、实用、可靠的优点，而被广泛应用于电力拖动领域。但是在低压电机驱动控制系统中，由于电机的转速范围和动态性能直接取决于逆变器输出电压［1］的范围和品质，因此为了提高电机的性能，通常采用过调制［2－3］方式以提高电源电压利用率。

传统的空间矢量脉宽过调制中，控制角的计算往往不够准确，而且满足不了调制比0～1的变化范围，影响了电压的输出能力。

本文基于面积等效原理提出的过调制控制角的新算法计算简单、准确，存储量小，程序执行时间短，能够完成从线性调制到过调制中六阶梯波工作状态［4－5］的平滑过渡，并具有良好的线性增益。

1 SVPWM过调制

定义m=|Ur|/|Usix|为SVPWM的调制比(0≤m≤1)，其中Ur为给定电压矢量，Usix为6拍时的电压矢量。当空间电压矢量落在过调制Ⅰ区和过调制Ⅱ区时，控制方法有所不同，以下将针对两种情况分别进行讨论。

1.1 过调制Ⅰ区控制算法

如图1所示，调制基本准则为:超出正六边形边界的电压矢量部分减小其幅值，使其落在边界线上，如图1的BC和DE段;未超出边界部分提高其电压输出矢量，以补偿超出正六边形边界时的电压损失［6］。这样，在一个SVPWM周期中，补偿后的电压矢量与给定电压矢量相比，只是幅值上有所变化，相角不曾改变，二者是同步关系。其中α的大小与调制比的变化有关。当α等于最大值π/6时，空间电压矢量轨迹为正六边形内切圆，此时达到线性调制的极限状态，调制比m=0.866;当α等于最小值0时，调制比m=0.909，空间电压矢量轨迹为正六边形，此时达到过调制方式Ⅰ的极限状态［7－8］。

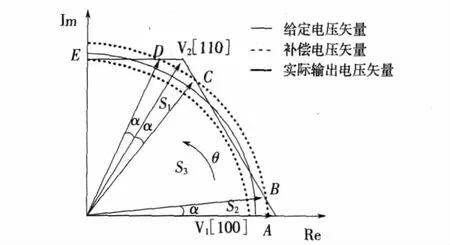
图1 过调制Ⅰ区控制算法Fig．1 Control algorithm of over modulation region Ⅰ

根据面积等效原理，给定电压矢量Ur对于时间的积分为细实线的面积，而令过调制处理后的输出电压矢量的积分面积与其相等，则可有相同的矢量作用效果。设给定电压矢量对应的作用面积为S，α度对应的两扇形面积分别为S1和S2，中间角度对应面积为 S3，有 S=S1+S2+S3，即整理得

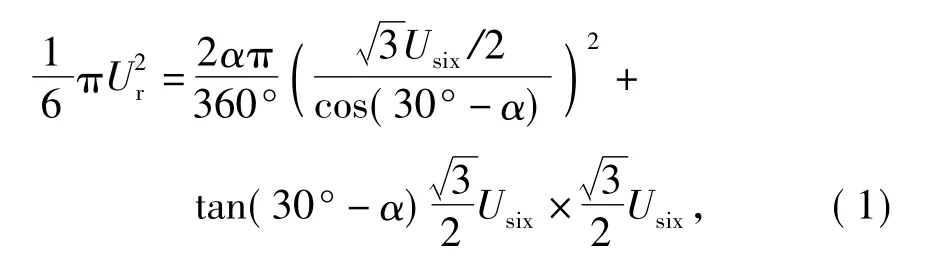
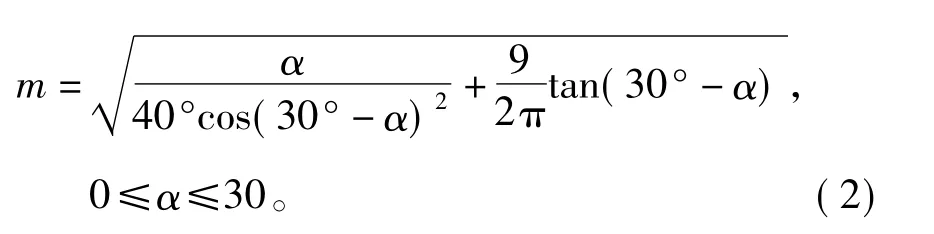
1.2 过调制Ⅱ区控制算法

如果继续增加调制比，将没有区域可以对电压进行补偿，因此将进入过调制Ⅱ区。如图2所示，虚线为正六边形内切圆，代表线性调制区的极限状态。此时输出电压矢量先保持为基本电压矢量Usix，当给定电压矢量旋转过β度时，再以与给定电压矢量同步的相位关系沿六边形的边沿输出，每扇区的最后β度仍输出基本电压矢量［9］。与过调制方式Ⅰ不同，在一个PWM周期内，经过电压补偿后的空间电压矢量和给定空间电压矢量相比，幅值改变且相角发生跳变。控制角β的变化取决于调制比的变化，β取最小值0时，实际输出电压轨迹为正六边形，达到过调制模式Ⅰ的极限状态;β取最大值π/3时，实际输出电压为六阶梯波，调制比m为1，达到过调制模式Ⅱ的极限状态［10］。根据面积等效原理得

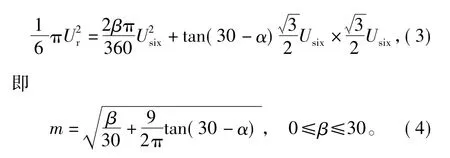
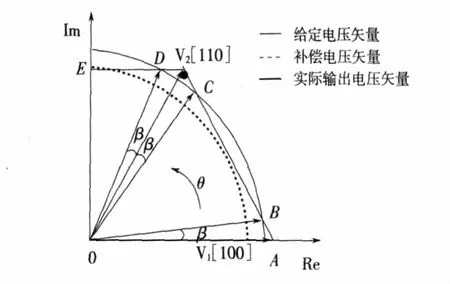
图2 过调制Ⅱ区控制算法Fig．2 Control algorithm of over modulation region Ⅱ

1.3 控制角α、β的计算

在传统的过调制算法中，控制角α、β的计算往往不够精确，甚至不能使调制比m达到0～1区间内的某些上限值。基于面积等效原理的SVPWM过调制算法中，α、β角度值在C语言编程环境中迭代法求取最优解，使m在一定精度下取遍0～1区间内的任意值。求得α、β角度值及其对应的调制比m如表1所示。

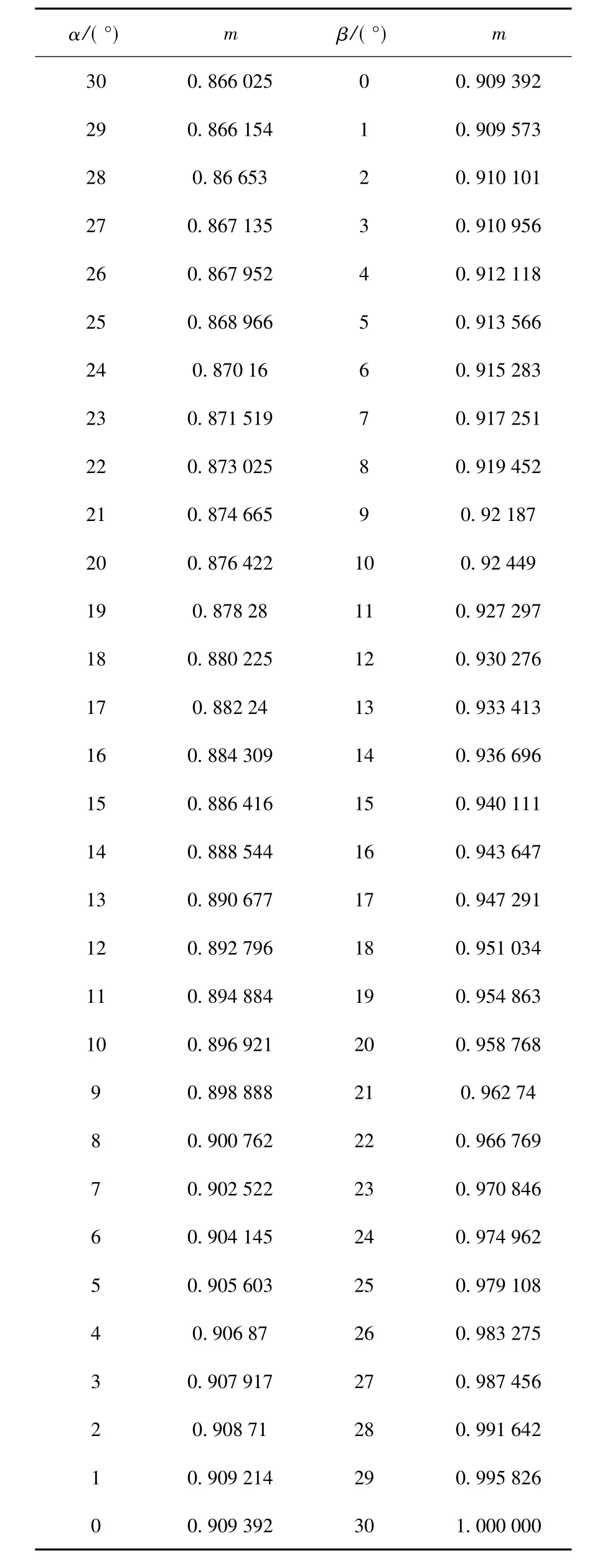
表1 控制角α、β及其对应的调制比mTable 1 Control angle α，β and the corresponding modulation ratio m

1.4 新旧算法对比

传统控制角算法中，可得

新旧控制角α、β算法下相应的调制比m对比如图3、4所示，实线为新算法下的调制比，虚线为旧算法下的调制比。

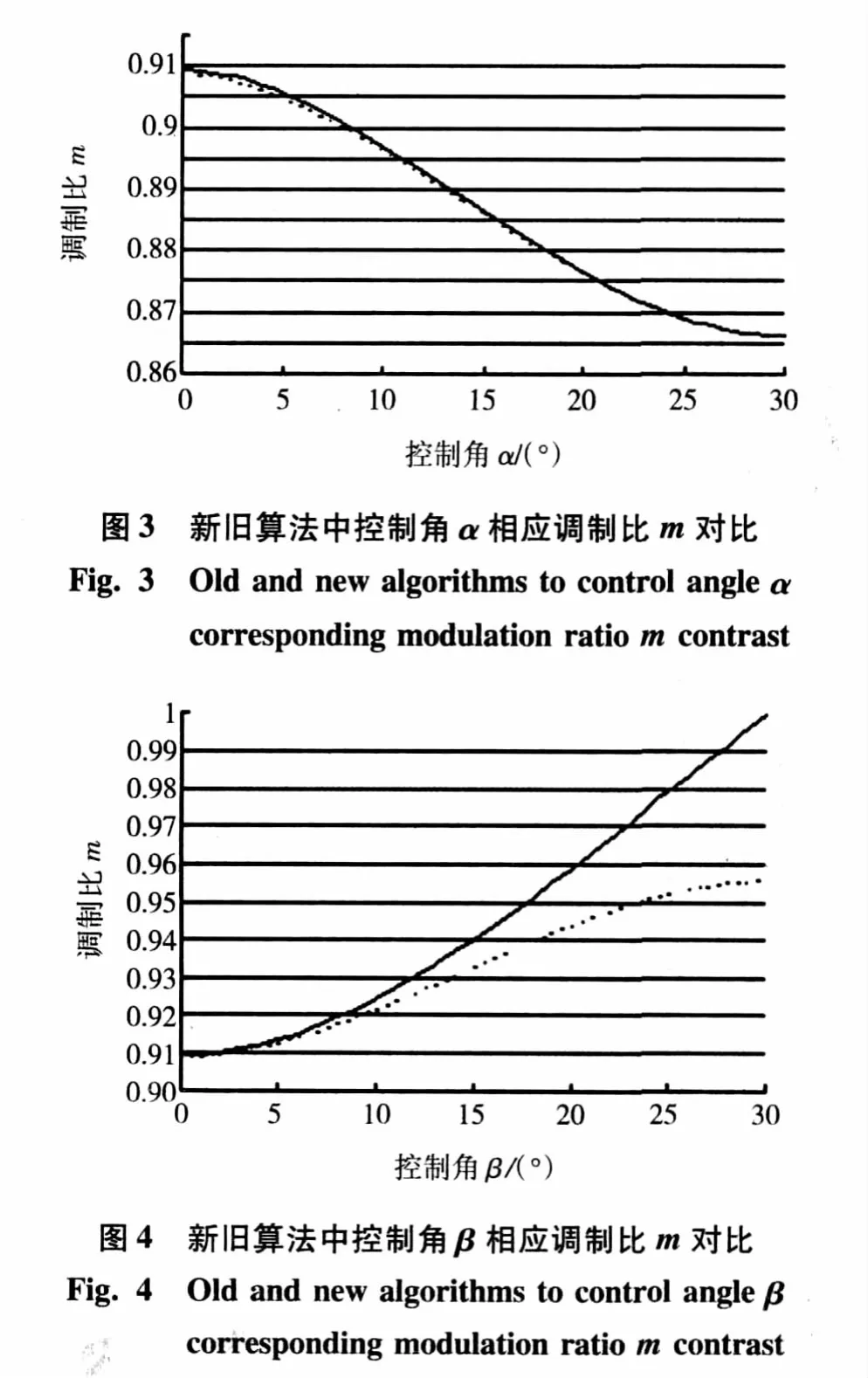
由图4可见，在过调制Ⅰ区中，新旧算法所对应的调制比所差不多，基本重合，而在过调制Ⅱ区中，新算法的调制比明显优于旧算法，当控制角β为30°时，调制比接近于1，将很大程度上提高电压利用率。

2 SVPWM过调制算法仿真

采用Matlab/SIMULNK建立了仿真模型，其中SVPWM过调制模块如图5所示。

以12V电励磁同步电机在20N·m的负载条件下，调节调制比 m 从 0.866、0.893、0.919、0.946、0.974到1.000，得到其线电压各个仿真波形如图6(a)、(b)、(c)、(d)、(e)、(f)所示。

由图6可见，线电压随着调制比的增大，呈现了由线性调制到六阶梯波极限状态的渐变过程，具有良好的线性增益。

3 实现方法

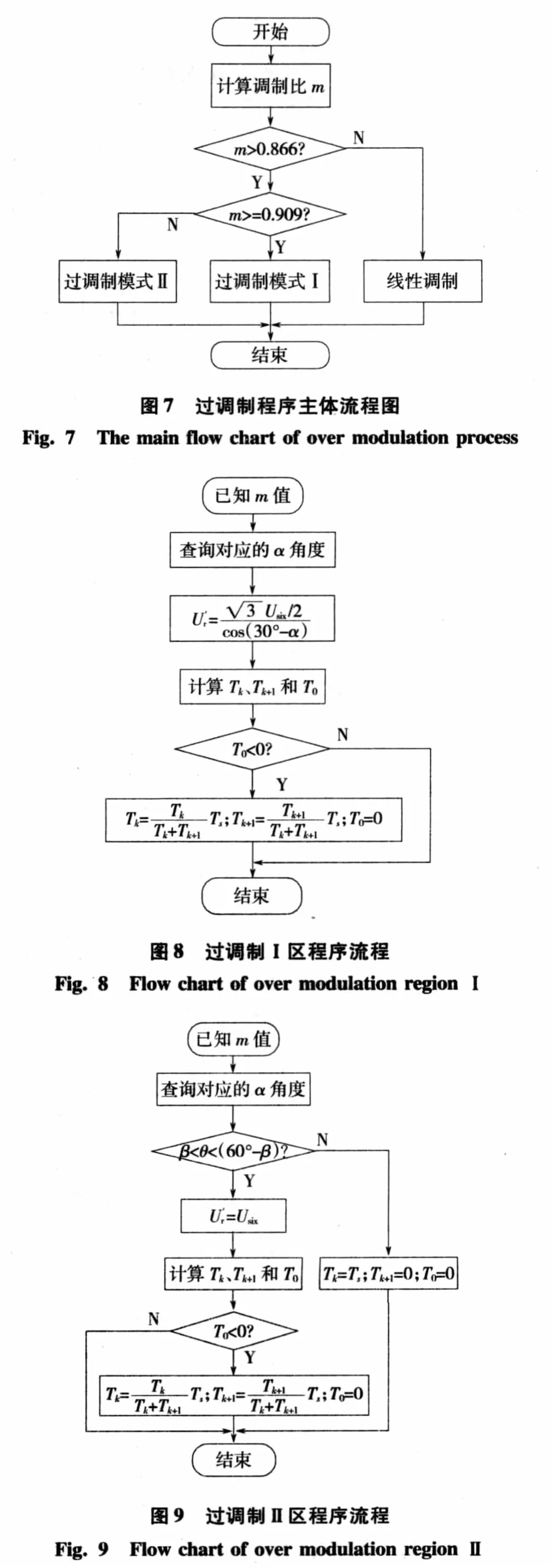
存储控制角α、β与调制比m的数值对应表，编写SVPWM过调制控制程序，流程图如图7、图8和图9所示。

与不加入过调制的程序相比所用执行时间分别如图10和图11所示。其中高电平区间为相关程序执行时间，未加入过调制的程序执行时间为37 μs，加入过调制算法的程序执行时间为39 μs，可见过调制程序的加入不会影响整体程序的执行效率。

4 实验结果

基于SVPWM过调制技术的理论分析及仿真结果，在12V BSG电励磁同步电机驱动系统上进行具体实验验证，逆变器选用MOSFET为开关器件，采用基于磁场定向的矢量控制作为电机的控制策略，核心控制单元为DSP2812，直流母线电压为12.12 V，略高于电机在额定点正常工作时所需的直流母线电压。

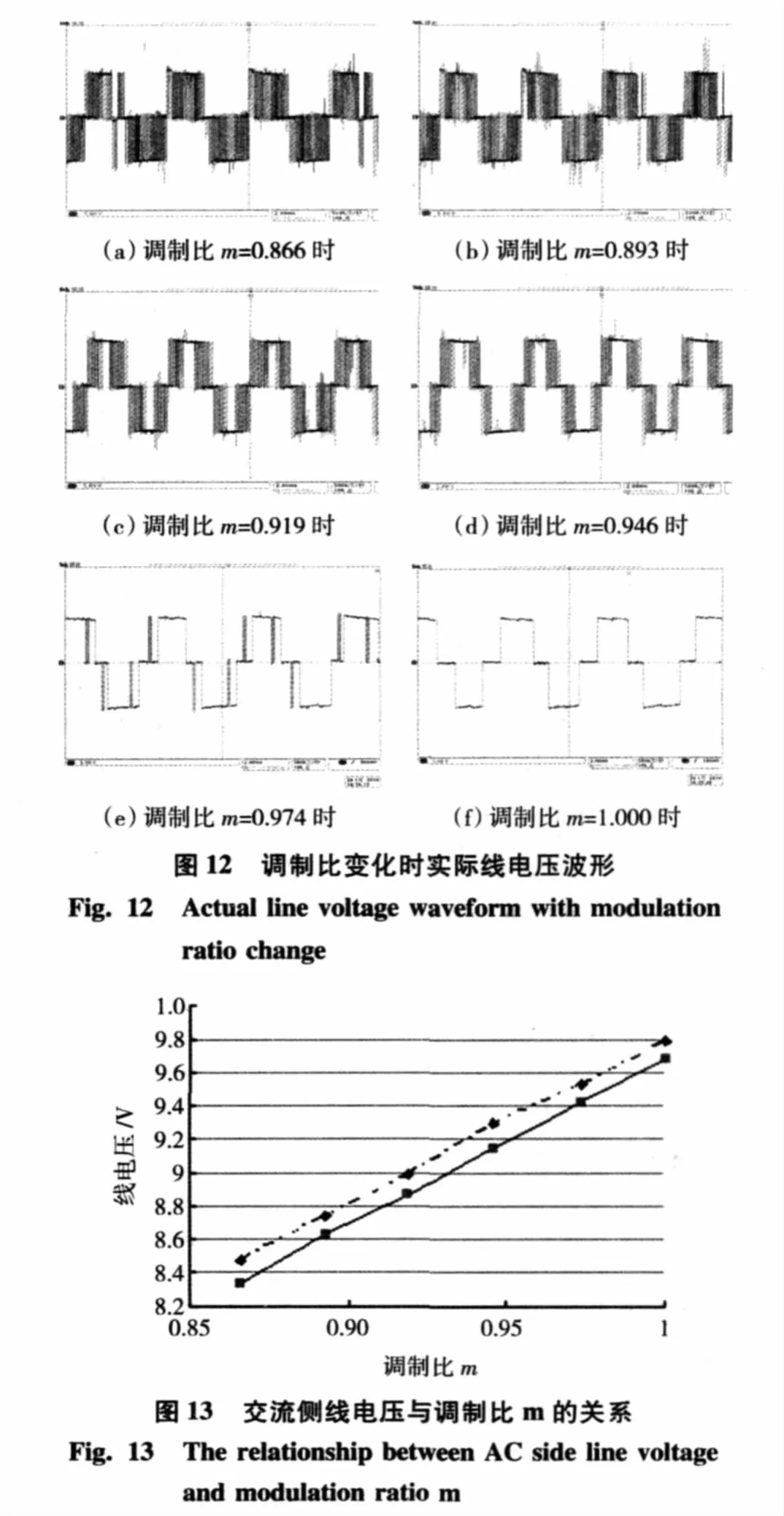
在负载为20 N·m时，随着调制比的从0.866、0.893、0.919、0.946、0.974 到 1.000，加入过调制算法的线电压波形如图 12(a)、(b)、(c)、(d)、(e)、(f)所示。

交流侧线电压与调制比m的关系如图13所示。图中虚线是仿真线电压有效值数据曲线，实线为实际线电压有效值数据曲线，可见二者均与调制比m成线性关系。由于电机驱动控制器等的损耗存在，实际输出线电压在幅值上略低于理论数据。

5 结语

由实验数据和实际线电压波形，可见本文所提出的SVPWM过调制控制角算法技术在车用12V BSG电励磁同步电机驱动系统上可以完成由线性调制到六阶梯波极限状态的平滑过渡，电机运行稳定，提高了直流母线电压利用率，是扩展电机转速范围、增加最大输出转矩的一种有效方法。

［1］ 张立伟，刘钧，温旭辉，等．基于基波电压幅值线性输出控制的SVPWM过调制新算法［J］．中国电机工程学报，2005，25(19):12－18．ZHANG Liwei，LIU Jun，WEN Xuhui，et al．A novel algorithm of SVPWM inverter in the over modulation region based on fundamental voltage amplitude linear output control［J］．Proceedings of the CSEE，2005，25(19):12 －18．

［2］ 杨贵杰，孙力，崔乃正，等．空间矢量脉宽调制方法的研究［J］．中国电机工程学报，2001，21(5):79 －83．YANG Guijie，SUN Li，CUI Naizheng，et al．Study on method of the space vectir PWM［J］．Proceedings of the CSEE，2001，21(5):79－83．

［3］ 张立伟，温旭辉，陈桂兰，等．一种新颖的分段连续控制SVPWM 过调制算法［J］．电机与控制应用，2005，32(7):19 －23．ZHANG Liwei，WEN Xuhu，CHEN Guilan，et al．A novel subsectional continuous control strategy of SVPWM inverter in overmodulation region［J］．Electric Machines＆ Control Application，2005，32(7):19－23．

［4］ SHINHWIBeon．New antiwindup PI controller for variable-speed motordrives［J］．IEEE Trans on Ind Elec，1998，45(3):445－450．

［5］ MONDAL SK，PINTO JOP，BOSE B K．A neural-network based space vector PWM controller for a three-level voltage-fed inverter inductionmotor drive［J］．IEEE Tram ind Applicat，2002，38(3):660－669．

［6］ LEE D C．A novel overmodulation technique for space vector PWM inverters［J］．IEEE Transactions on Power Electronics，1998，13(6):1144－1150．

［7］ BOLOGNANI S．Novel digital continuous control of SVM inverters in the overmodulation range［J］．IEEE Transactions on Industry Applications，1997，33(2):525 －530．

［8］ HOLTZ J．Pulse width modulation-a survey［J］．IEEE Transaction on Industry Electron，1992，39(6):410 －420．

［9］ HOLTZ J．On continuous control of PWM inverters in the over modulation range including the six-step mode［J］．IEEE Transactions on Power Electronics，1993，8(4):546 －552．

［10］ PARK HeeJhung，YOUN MyungJoong．A new time-domain discontinu-ous space-vector PWM technique in overmodulation region［J］．IEEE Trans on IE，2003，50(2):349 －355．