1.5MW永磁风力发电机电磁场与温度场计算与分析

李伟力， 程鹏， 张美巍， 祝令帅， 伊然

(1．哈尔滨理工大学电气与电子工程学院，黑龙江哈尔滨150080;2．哈尔滨工程大学自动化学院，黑龙江哈尔滨150001)

0 引言

目前国际上风力发电机技术发展迅速，主要特点有:向更大的单机容量方向发展;研发新型机组结构形式和材料;开始对海上专用风电进行开发探索［1－3］。随着风电政策的逐渐完善，我国风电产业方兴未艾，未来很长一段时间都将保持高速发展。如今新装机的风电场，基本上以兆瓦级以上的风力发电机为主［4］。

兆瓦级风力发电机主要包括双馈型风力发电机、直驱式永磁风力发电机和半直驱式永磁风力发电机。我国的兆瓦级直驱和半直驱永磁风力发电机在设计与制造水平上与国外还有一定的差距［5］。国内部分高校的一些专家和学者进行了较为深入的理论研究工作，为兆瓦级永磁风力发电机的研究与设计奠定了理论基础［6－11］。但是，很少研究兆瓦级永磁同步风力发电机温度分布及相关变化情况，这是永磁同步发电机设计者很关心的一个问题。因此研究兆瓦级风力发电机内温升对电机安全运行具有重要的意义。

本文根据以上基础理论进一步深化，设计了3台32极、不同定子槽数、不同结构尺寸的1.5MW永磁半直驱同步风力发电机，建立电磁场与温度场有限元数学模型，对永磁半直驱同步风力发电机电磁场与温度场进行了计算。研究了空载与负载两种工况下电磁场分布、温度场及相关因素的关系，并对一台相似结构的小型永磁同步风力发电机的实测数据与理论计算结果进行比较，为设计大容量永磁半直驱风力发电机提供了一些有意义的结论［12－14］。

1 1.5MW永磁半直驱同步风力发电机有限元模型的建立与分析

表1 1.5MW永磁半直驱同步风力发电机设计数据Table 1 Design data of 1.5MW half-direct permanent magnet synchronous wind generator

考虑到兆瓦级永磁同步发电机的实际结构特点，为计算方便，对兆瓦级永磁同步发电机的计算区域作如下假设［6，15］:

1)用二维电磁场来模拟实际磁场，不计电机外部磁场，不考虑位移电流的影响，电流密度和磁矢位只有Z轴方向的分量;

2)电枢铁心的磁导率无穷大，即μFe=∞;

3)忽略电导率和磁导率的温度效应，它们仅为空间函数，铁磁材料的磁滞效应忽略不计。

考虑到兆瓦级风力发电机在工程吊装和高空运行时的安全性与稳定性，所设计的电机均采用轮毂式转子结构，目的是减重。3种电机的结构相类似，只给出32极144槽方案的物理模型及其求解域，如图1所示。

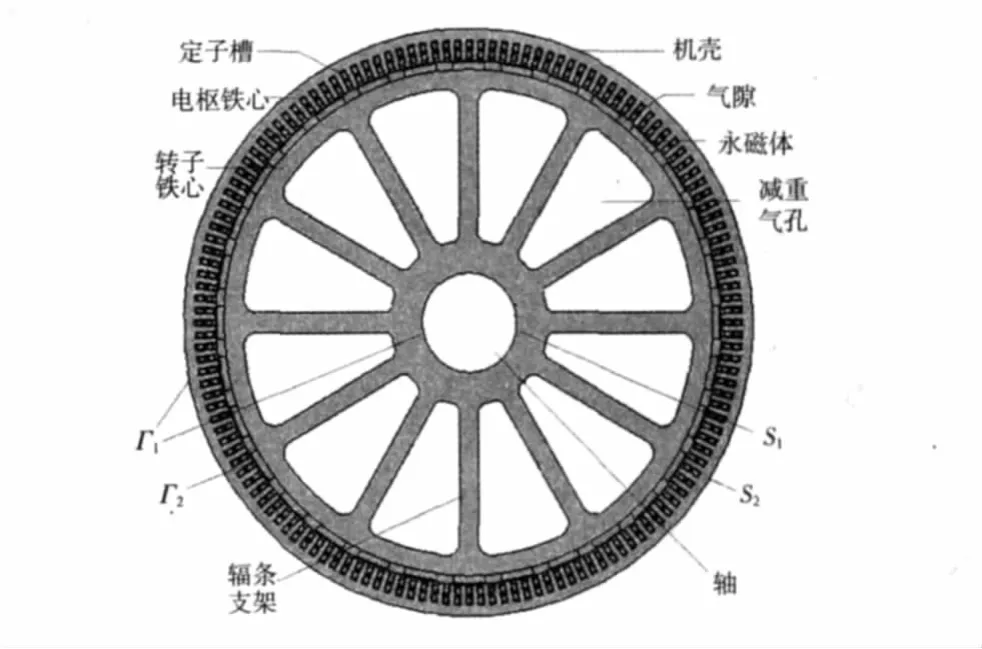
图1 电机物理模型Fig．1 Physical model of generator

由于半直驱永磁同步发电机的轴向对称性，故采用二维静态电磁场进行计算，并取电机整个横截面为求解域，则静态平面电磁场满足下列泊松方程边值问题［6，15］，即

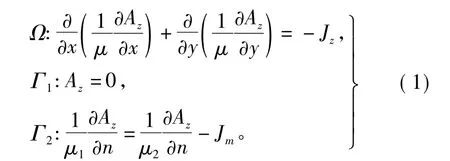
式中:Ω为求解区域;Az为矢量磁位;Jz为电流密度;μ为磁导率;Γ1为第一类边界条件;Γ2为永磁体等效面电流边界;Jm为永磁边界等效面电流密度;μ1、μ2分别为永磁边界两材料的磁导率。

把定子外表面和转子内径表面Γ1作为边界面，边界上磁力线闭合，属一类强加边界条件，令其上的矢量磁位Az=0。

由于永磁同步发电机由永磁体励磁，气隙磁场谐波较多，使电动势中的谐波也较多，所设计的绕组均采用星形联结的双层短距三相绕组，避免发电机绕组中产生环流。永磁同步发电机的绕组匝数和线规可根据发电机的电磁负荷、电流密度和定子槽型尺寸的限制来确定［16］。在计算了定子绕组的导体相对高度，最小齿宽之后，选择了如表2中的3个电枢绕组方案进行计算分析。

表2 部分绕组设计参数Table 2 Design parameters of machine winding

文中3个方案均选用定子矩形槽，永磁体表面贴磁的转子结构(永磁体呈瓦片形)，永磁体采用钕铁硼。为了方便起见，在后文中出现的方案1，方案2和方案3分别代表32极144槽电机，32极156槽电机和32极252槽电机。

2 负载电磁场的计算与分析

2.1 负载电磁场分析

基于有限元的基本原理，计算了3台1.5MW半直驱永磁同步风力发电机稳态运行时的负载电磁场，得到了负载电磁场分布图，如图2、图3和图4所示。

经计算文中3个方案负载时齿顶磁密分别为1.47T、1.56T和1.43T;距1/3齿顶处磁密分别为1.44T、1.52T和 1.4T;齿根的磁密分别为 1.4T、1.45T和1.35T;定子轭部的磁密分别为1.05T、1.14T和0.76T。可见，铁心内磁密均没有达到高饱和度。对电机工作在负载工况下的径向气隙磁密进行谐波分解，得到气隙磁密基波和各次谐波的幅值，图5分别列出了3种方案各取一个单元电机内的负载气隙磁密谐波分解图，如图5(a)、5(b)、5(c)所示。图6为负载气隙磁密的谐波含量分布。

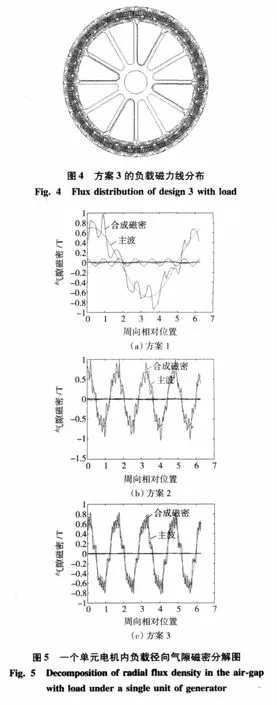
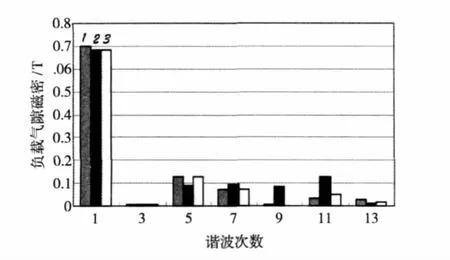
图6 负载气隙磁密的谐波含量分布Fig．6 Harmonic distribution of radial flux density in the air-gap with load

由图6的谐波含量分布图可知，3个方案的气隙基波磁密幅值相差不大，基波的含量远大于谐波的含量。在谐波中，3个方案的3次谐波含量几乎为零，13次谐波都较小。方案2中的7次、9次和11次谐波稍大，方案1和方案3中的5次谐波稍大。

2.2 相似类型结构的小型永磁同步风力发电机的实测数据与理论计算结果的比较

为了验证兆瓦级永磁同步发电机计算方法的正确性，制作了一台相似结构的小型永磁同步风力发电机，相比兆瓦级半直驱永磁同步风力发电机的输出电压不同，结构形状相似，整体尺寸缩小了，冷却方式相同，其物理模型如图7所示。应用与计算兆瓦级半直驱永磁同步风力发电机相同的方法，建立小型风力发电机的有限元模型并进行仿真计算，文中给出了电机的负载磁力线分布图，如图8所示，并对比了实测数据与理论计算结果，如表3所示。

由对比数据可知，理论计算值与实测值接近，误差较小，计算结果较为准确，验证了计算方法的正确性。因此本文将此理论计算方法运用到兆瓦级永磁同步风力发电机的参数计算中，为设计大容量永磁半直驱风力发电机提供了一些有意义的参考。经验证，永磁体表面贴磁的转子结构与插入式转子结构对漏磁有一定影响，但影响不大。

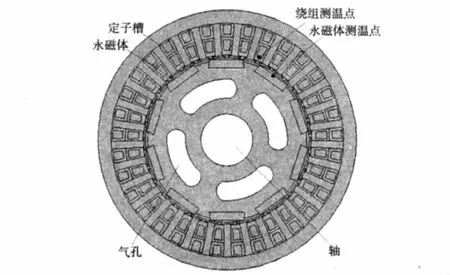
图7 电机物理模型Fig．7 Physical model of generator

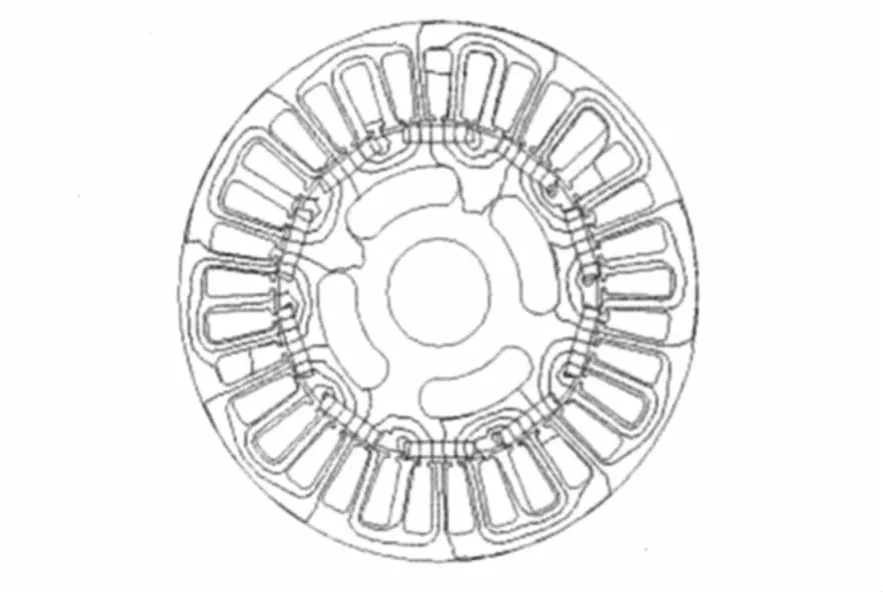
图8 负载磁力线分布Fig．8 Flux distribution with load

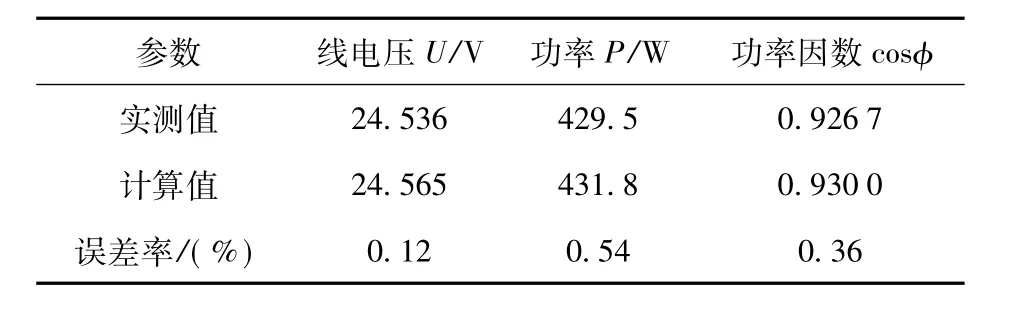
表3 实测数值与计算结果对比Table 3 Comparisons of the analysis results and test data

3 二维温度场的计算与分析

3.1 基本假设和温度场求解区域的确定

分别对三台1.5MW永磁半直驱同步风力发电机的二维温度场进行了理论计算。三台风力发电机都采用机壳外部自然风冷却，内部无轴向通风系统、定转子内无径向通风沟，无风扇，可以把三维温度场问题转化为二维温度场问题求解［17－19］，建立二维温度场模型，做如下基本假设:①电机沿轴向的热流密度为零［18－19］;②定子槽楔近似当作与槽同宽，槽内股线绝缘和层间绝缘的热性能与主绝缘相同;③忽略转子轴和轮毂铁心支架之间的热传递。

求解区域如图1所示。图中S1表示转子内径表面，S2为定子外表面。

在各向同性煤质中，导热系数为常数，在直角坐标下的二维稳态传导方程［20］为

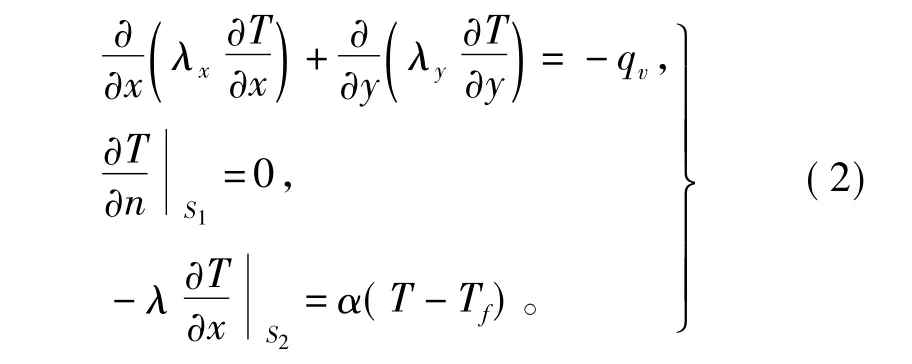
式中:T为求解区域任意位置处的温度;λx，λy为x，y方向的导热系数;qv为热源密度，它是各项损耗密度之和。对S1给出第二类边界条件;机壳表面为对流散热，对S2给出第三类边界条件，n为机壳表面单位法向量，α为散热系数，Tf为环境温度。根据变分原理，上述边值问题可转化为条件变分形式，对变分作离散化处理后，可得到二维温度场有限元方程，进而可以得到求解域内各个节点温度值。

根据电磁损耗的相关公式可以确定电机内各部分的损耗［16］。在计算电机全域温度场时，由于转子的旋转使气隙中的空气以湍流方式流动，导致了电机内部复杂的热交换，为了简化计算，引入了有效导热系数［19］，是用静止流体的导热系数来描述流动流体的导热性能，3台电机的气隙有效导热系数分别为0.253W/m·K，0.253W/m·K，0.322W/m·K。

3.2 基于流体与传热方法的温度场计算与分析

根据流体与传热理论，采用有限体积法计算出定子表面流场流速的分布，进而确定出定子表面散热系数，并把所得出的定子表面散热系数代入温度场进行计算得到电机内的各部分的温度［21－22］，文中给出了3台电机在15m/s风速下的温度分布图，如图9所示。

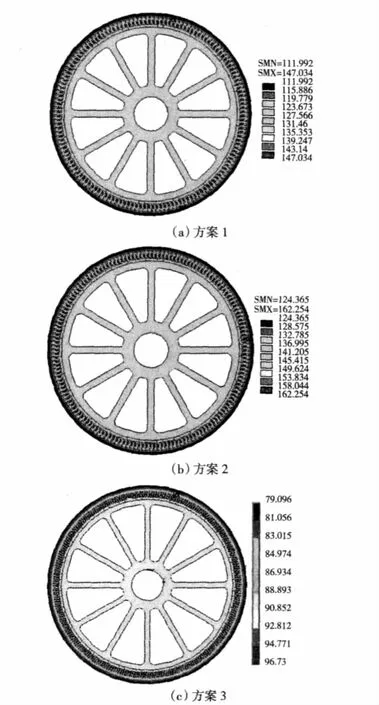
图9 发电机负载温度场分布Fig．9 Temperature distribution with load of generator

从图9的温度分布图可以看出，当风速为15m/s时，3个方案的定转子温度分布趋势大致相同，都是最高温度出现在上层绕组处，转子表面及轮毂温度次之，机壳表面的温度最低。文中的电机采用F级绝缘等级，绝缘材料允许工作到155℃。其中，方案2的最高温度达到162℃，超出F级绝缘等级要求的最高温度，可以将此电机的绝缘等级提高到H级，或者降低绕组电负荷来达到F级绝缘要求。本文将各方案电机主要部位的温度值列表，如表4所示。

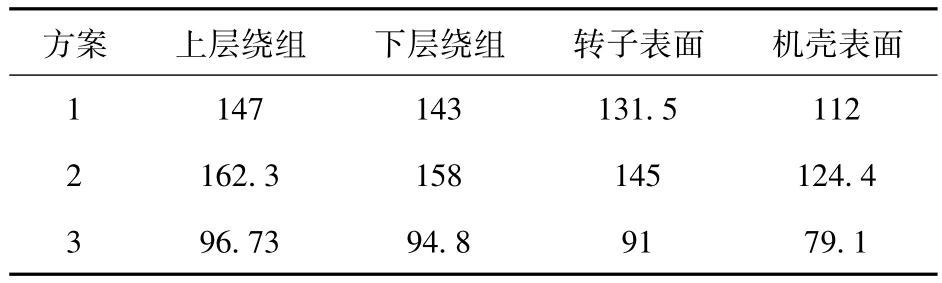
表4 3个方案电机的主要位置温度值Table 4 Temperature of different generator ℃

从表4中的温度数据可以看出，3个方案中电机的最高温度都出现在定子上层绕组上，温度值从上层绕组、下层绕组、转子表面、机壳表面依次呈递减趋势。

3.3 同类型小型永磁同步风力发电机温度场实测值与计算结果的对比

小型风力发电机机壳外部通有自然风冷却，内部无冷却系统，与兆瓦级半直驱永磁同步风力发电机的冷却方式相同。试验中实际测量了小型风力发电机机壳表面外加的8m/s风速和电机内定子绕组与转子永磁体等重要部位的温度。在计算小型风力发电机温度场时，用流体场数值方法计算得到了机壳表面的散热系数，然后通过温度场理论计算得到电机内的温度分布。文中给出了负载温度场分布图，如图10所示。

图10 流体与传热方法得散热系数时负载温度场分布Fig．10 Temperature distribution base on the heat transfer coefficients determined from fluid and heat transfer theories with load

表5中给出了用流体与传热学理论方法计算得到散热系数时的温度场计算结果与实测温度值的比较。

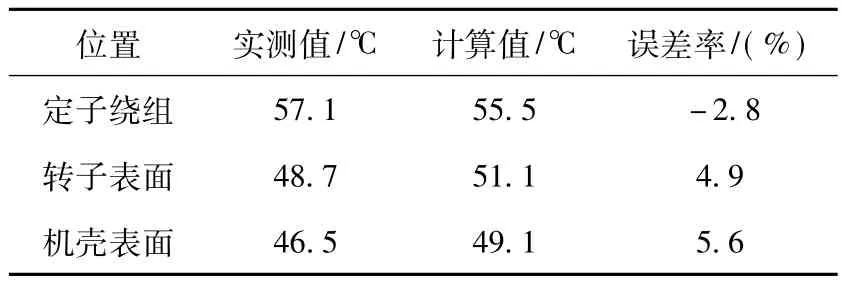
表5 实测温度值与计算结果对比Table 5 Temperature comparisons of the analysis results and test data

从表5中的对比结果可以看到，用流体场传热方法得到散热系数时的温度场结果与实测值误差较小，该方法较为准确。以上通过对同类型小型风力发电机的理论计算，可以为设计大容量永磁半直驱风力发电机提供了一些有意义的理论参考。

4 结论

1)文所设计的3个电机方案中，由于电机极槽匹配关系与电机绕组匝数不同以及其它原因，3种方案所产生的损耗不同，方案2(32极156槽电机)的谐波含量较大，电机的损耗也较大，使其热负荷较高，导致了电机内温度比其他两方案都高。

2)通过对3个方案电机内负载温度场的计算与分析可以看出，3个方案中电机内的最高温度均出现在定子上层绕组处，最低温度在机壳表面处。方案1中定子上层绕组温度比下层绕组温度高了4℃，最高温度值与最低温度值相差35℃;方案2的定子上层绕组温度值比下层绕组温度值高了4.3℃，最高温度值与最低温度值相差37.9℃;方案3的定子上层绕组温度值比下层绕组温度值高出1.93℃，最高温度与最低温度相差17.63℃。

3)计算小型风力发电机的温度场时，采用了流体场数值方法计算了定子表面散热系数，并把温度场的计算值与实测值进行比较，结果表明，用流体场数值方法计算得到散热系数时，电机内的温度场计算值与实测值相差比较小。

4)小功率的风力发电机进行试验和理论计算，验证了计算方法的准确性，可将此计算方法推广到与小功率风力发电机相似结构的兆瓦级永磁风力发电机的电磁计算和热计算中。

［1］ 王承熙，张源．风力发电［M］．北京:中国电力出版社，2003．

［2］ 姚润丰．近海7.5亿千瓦巨额风能亟待开发利用［M］．北京:新华社，2005．

［3］ 李俊峰，高虎，王仲颖，等．中国风力发展报告2008［R］．北京:中国环境科学出版社，2008．

［4］ 隋红霞．双馈风力发电机组接入电网特性研究［D］．辽宁:沈阳工业大学，2008．

［5］ 刘婷．直驱永磁同步风力发电机的设计研究［D］．长沙:湖南大学，2009．

［6］ 唐任远．现代永磁电机理论与设计［M］．北京:机械工业出版社，2002．

［7］ 王秀和．永磁电机［M］．北京:中国电力出版社，2007:8－85．

［8］ 李钟明．稀土永磁电机［M］．北京:国防工业出版社，1999．

［9］ 张岳，王凤翔．直驱式永磁同步风力发电机性能研究［J］．电机与控制学报，2009，13(1):79 －82．ZHANG Yue，WANG Fengxiang．Performance research on permanent magnet synchronous generator directly driven by wind turbine［J］．Electric Machines and Control，2009，13(1):79 －82．

［10］ 邓秋玲，黄守道，彭磊．直驱低速2MW永磁同步风力发电机设计和有限元分析［J］．微电机，2009，42(7):9 －12．HUANG Shoudao，DENG Qiuling，PENG Lei．FEM analysis and design on low speed direct driven permanent magnet generator for wind turbine［J］．Micromotors，2009，42(7):9 － 12．

［11］ 张兆强．永磁同步风力发电机的有限元分析［J］．大电机技术，2007，(5):18 －21．ZHANG Zhaoqiang．Finite element analysis for permanent magnet synchronous generator［J］．Large Electric Machine and Hydraulic Turbine，2007，(5):18 －21．

［12］ 陈阳生，林友仰．永磁电机气隙磁密的分析计算［J］．中国电机工程学报，1994，14(5):17 －26．CHEN Yangsheng，LIN Youyang．Calculation of air-gap flux density in permanent magnet machines［J］．Proceedings of the CSEE，1994，14(5):17－26．

［13］ 赵强，赵争鸣，高徐娇．永磁电机中永磁体尺寸优化设计［J］．电机电器技术，2001，(3):2－5．ZHAO Qiang，ZHAO Zhengming，GAO Xujiao．Design permanent-magnet material of permanent-magnetic synchronous motor［J］． Electric Machine and Electric Apparatus Technologies，2001，(3):2－5．

［14］ 谢颖，李伟力，李守法．异步电动机转子断条故障运行时定转子温度场数值计算与分析［J］．电工技术学报，2008，23(10):33－39．XIE Ying，LI Weili，LI Shoufa．Calculation and analysis of temperature field for induction motors with broken bars fault［J］．Transactions of China Electrotechnical Society，2008，23(10):33－39．

［15］ 汤蕴璆．电机内的电磁场［M］．2版．北京:科学出版社，1998:265－280．

［16］ 陈世坤．电机设计［M］．2版．北京:机械工业出版社，2000．

［17］ CHEN J，NAYAR C V，XU L．Design and finite-element analysis of an outer-rotor permanent-magnet generator for directly couple wind turbines［J］．IEEE Transactions on Magnetics，2000，36(5):3802－3809．

［18］ XYPTERAS J，HATZIATHANASSIOU V．Thermal analysis of an electrical machine taking into account the iron losses and the deep-bar effect［J］．IEEE Transactions on Energy Conversion，1999，14(4):996－1003．

［19］ HATZIATHANASSIOU V，XYPTERAS J，Archontoulakis G．E-lectrical-thermal coupled calculation of an synchronous machine［J］．Archiv Fur Elektrotechnik，1994，77:117 －122．

［20］ 李伟力，李守法，谢颖，等．感应电动机定转子全域温度场数值计算及相关因素敏感性分析［J］．中国电机工程学报，2007，27(24):86 －87．LI Weili，LI Shoufa，XIE Ying，et al．Stator-rotor coupled thermal field numerical calculation of induction motors and correlated factors sensitivity analysis［J］．Proceedings of the CSEE，2007，27(24):86－87．

［21］ 鲍里先科A N．电机中的空气动力学与热传递［M］．北京:机械工业出版社，1985．

［22］ 李伟力，丁树业，靳慧勇．基于耦合场的大型同步发电机定子温度场的数值计算［J］．中国电机工程学报，2005，25(13):129－134．LI Weili，DING Shuye，JIN Huiyong．Numerical calculation of large synchronous generator stator temperature fields based on coupled fields［J］．Proceedings of the CSEE，2005，25(13):129－134．