具有阶段结构和时滞的幼年染病单种群模型研究

石瑞青, 陈兰荪

(1.大连理工大学数学科学学院,辽宁大连 116024;2.山西师范大学数学与计算机科学学院,山西临汾 041004)

0 引 言

文献[1、2]研究了具有阶段结构的单种群模型,作者假设种群从幼年到成年的平均成熟期为一个常数,在模型中用一个时滞来表示.文献[1]的模型为

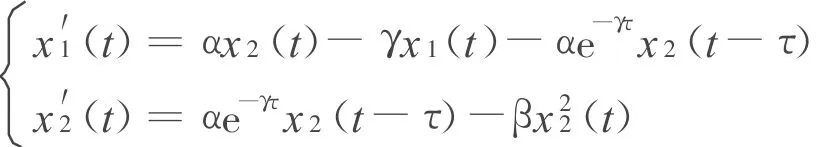
式中:x1(t)、x2(t)分别表示幼年和成年种群的密度;α>0,代表出生率;γ>0,是幼年的死亡率;β>0,代表成年种群的死亡率和密度制约;τ>0,表示成熟期.αe-γτx2(t-τ)表示在t-τ时刻出生的幼年(也就是αx2(t-τ))并且存活到时刻t的密度(由于幼年具有死亡率),因此,αe-γτx2(t-τ)表示从幼年到成年的转化率.

种群疾病的传播主要依赖于疾病本身的特性.例如麻疹、腮腺炎、水痘、猩红热、白喉等疾病主要在幼年种群中传播,而淋病、梅毒等传染病只在成年种群中传播.文献[3、4]考虑了具有阶段结构的单种群SIS流行病模型.文献[3]考虑的模型为

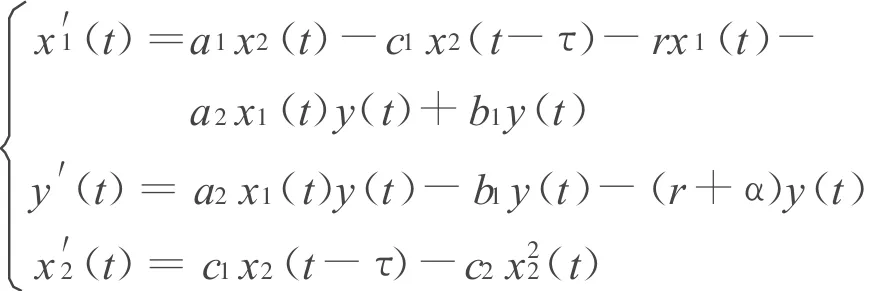
式中:x1(t)、y(t)表示易感幼年和染病幼年种群的密度;x2(t)表示成年种群的密度,流行病只在幼年种群中传染,而成年种群不会染病;a1表示幼年的出生率;a2是接触率;a2x1(t)y(t)表示双线性传染率;r表示幼年的自然死亡率;α表示因病死亡率;c1表示从幼年到成年的转化率;c2x2

2(t)表示成年具有Logistic型死亡率;b1表示染病幼年的康复率.其他参数的具体生物意义可以参看文献[1～4].

此外,文献[5、6]考虑了具有阶段结构单种群的收获策略.受文献[1、3]的启发,本文具体研究幼年染病具有阶段结构和时滞的单种群模型.

1 模型的建立及分析

1.1 模型建立

模型建立如下:

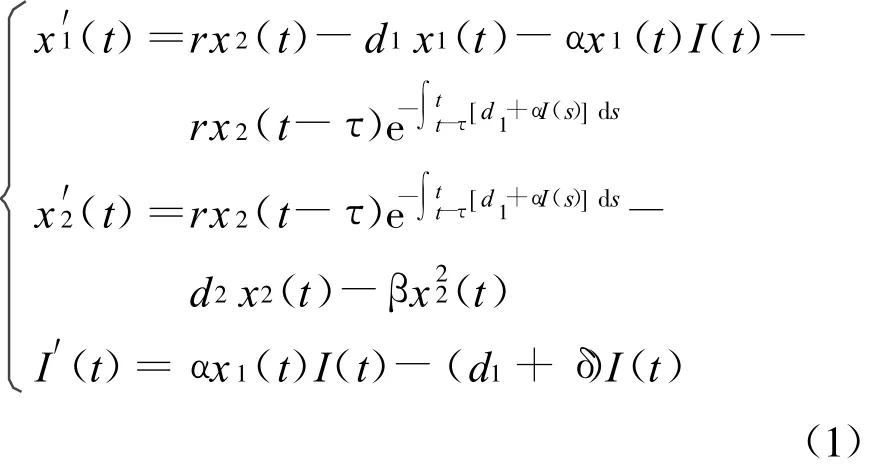
式中:x1(t)、I(t)分别表示易感幼年和染病幼年种群的密度;x2(t)表示成年种群的密度,流行病只在幼年种群中传染,而成年种群不会染病;α>0,是接触率;αx1(t)I(t)表示双线性传染率;β>0,表示成年种群的密度制约;δ>0,表示染病幼年种群的因病死亡率.其他参数的具体生物意义可以参看文献[1～4]模型解释.下面研究系统(1)平衡点的存在性及稳定性.

1.2 性质分析

通过计算,得到系统(1)以下平衡点:

(1)种群绝灭平衡点(平凡平衡点)P0(0,0,0)总是存在的.

(3)当R1=re-d1τ/d2>1, 且+r)<1时,存在唯一的地方病平衡点(正平衡点,这里是方程的唯一正根.

平衡点P0和P1的存在性是显然的,下证地方病平衡点的存在性和唯一性.正平衡点P2(x＊1,x＊2,I＊)满足代数方程组由方程组(2)的第3个方程,易得x1=(d1+δ)/α,由第2个方程得x2=(re-(d1+αI)τ-d2)/β,代入第1个方程得

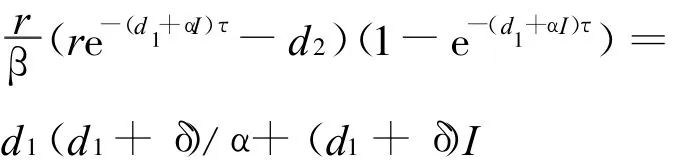
证明 (1)在P0处,特征方程为

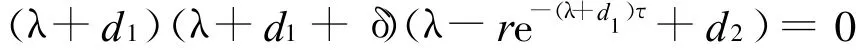
此特征方程的其中两个根为λ1=-d1<0,λ2=-(d1+δ)<0;特征根λ3由等式λ=re-(λ+d1)τd2决定.为了判断 λ3的符号,令f2(λ)=λ,g2(λ)=re-(λ+d21)τ-d,容易看出 ,f2(λ)在(0,+∞)上单调递增,g2(λ)在(0,+∞)上单调递减.

(A 1)当R1=re-d1τ/d2<1 时 ,f2(0)=0,g2(0)=re-d1τ-d2<0,所以 ,λ3为负数(见图1),对应地得出此时平衡点P0是局部渐近稳定的.

(A 2)当R1=re-d1τ/d2>1 时 ,f2(0)=0,g2(0)=re-d1τ-d2>0,所以,λ3为正数(类似于图2),平衡点P0是不稳定的.

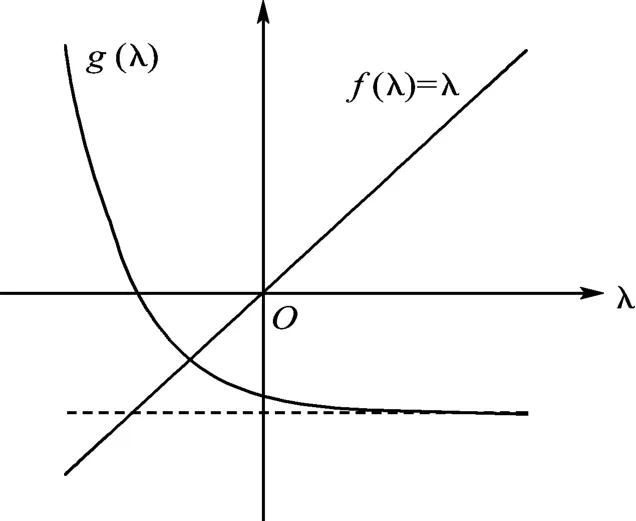
图1 交点为负的两条曲线Fig.1 The tw o curves with negative crossing-point

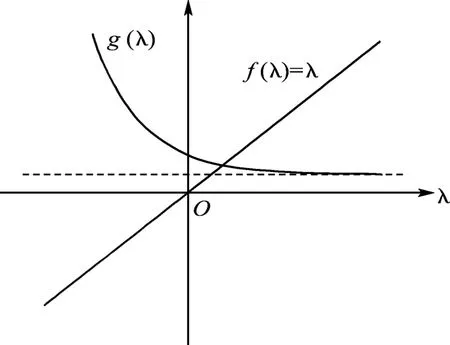
图2 交点为正的两条曲线Fig.2 The tw o curves with positive crossing-point

(2)在P1处,特征方程为

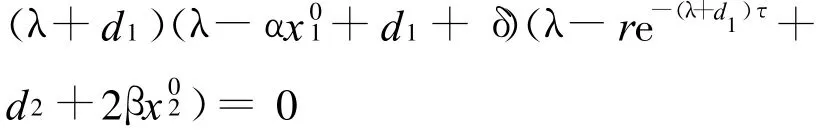
此特征方程的一个根为λ1=-d1<0,特征根 λ2由等式λ=re-(λ+d1)τ-d2-2βx02决定 ,第3个特征根 λ3=αx01-(d1+δ).为了判断 λ2的符号 ,令f3(λ)=λ,g3(λ)=re-(λ+d1)τ-d2-2β,则f3(λ)在(0,+∞)上单调递增,g3(λ)在(0,+∞)上单调递减 ,且f3(0)=0,g3(0)=re-d1τ-d2-2βx02=-βx02<0,所以,特征根λ2的符号为负(类似于图1).

(B1)当R1=re-d1τ/d2>1, 且时对应地得到此时平衡点P1是局部渐近稳定的.

(B2)当R1=re-d1τ/d2>1, 且时 ,(d1+δ)>0,对应地得到此时平衡点P1是不稳定的.

(3)在P2处,特征方程为

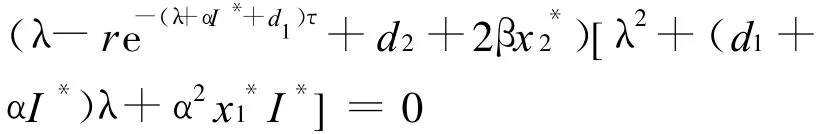
容易看出特征根 λ2、λ3满足λ2+λ3=-(d1+αI＊)<0,λ2λ3=αx1＊I＊>0,所以特征根λ2和λ3都具有负的实部.特征根 λ1由等式 λ=re-(λ+αI＊+d1)τ-d2-2βx2＊决定.为判断 λ1的符号,令f4(λ)=λ,g4(λ)=re-(λ+αI＊+d1)τ-d2-2βx2＊.容易看出f4(λ)在(0,+∞)上单调递增,g4(λ)在(0,+∞)上单调递减,并且f4(0)=0,g4(0)=re-(d1+αI＊)τ-d2-2βx2＊=-βx2＊<0.所以 ,特征根λ1的符号为负(类似于图 1).因此,平衡点P2存在、唯一并且是局部渐近稳定的.

1.3 模型平衡点的稳定性结论

关于3个平衡点的存在性和稳定性的结论总结见表1.

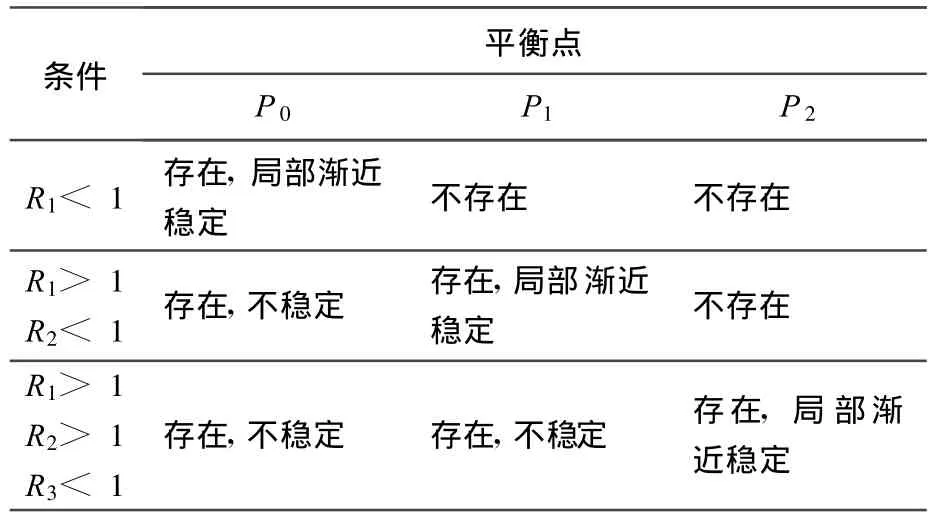
表1 平衡点的存在性和稳定性条件Tab.1 The existence and stability conditions for the equilibriums

推论 1 (1)令 τ0=-ln(d2/r)/d1,则当τ>τ0时,P0局部渐近稳定;当τ<τ0时,P0不稳定.

(2.1)当τ<τ0,且 Δ<0时,P1局部渐近稳定.

(3)当τ∈(τ3,τ1)时,P2是局部渐近稳定的.

证明 首先指出,τ0和 τ3总是存在的(在生物意义下,总是假设r>m ax{d1,d2});τ1和τ2存在的条件是 Δ>0.当 τ0 、τ1 、τ2 、τ3 都存在时 ,满足τ0>τ1>τ3>τ2>0.

(1)R1<1和τ>τ0是等价的;而且R1>1和τ<τ0是等价的.

因此(2.2)成立.

(3)当τ<τ0,Δ>0,且τ∈ (τ2,τ1)时另外 ,τ>τ3等价于而且 τ3 ∈ (τ2,τ1),所以,当τ∈(τ3,τ1)时 ,定理1的条件(3)满足,故P2是局部渐近稳定的.

推论2 由定理1和推论1,得到

(1)当 Δ<0时 ,τ0是一个阈值.若 τ>τ0,则P1不存在,P0局部渐近稳定;若τ<τ0,P0不稳定,P1存在而且局部渐近稳定.

(2)当Δ>0时,平衡点的稳定性由τ的不同取值区间决定 .若 τ∈ (0,τ2)∪ (τ1,τ0),P1是局部渐近稳定的 ;若 τ∈ (τ2,τ1),则P1不稳定;若τ∈(τ3,τ1),P2存在且是局部渐近稳定的.

1.4 例 题

例1 取 α=β=r=1,d1=0.3,d2=0.2,τ=2,若取 δ=0.2,则有R1=2.744>1,R2=1.350>1,R3=0.9147<1,根据定理1,地方病平衡点存在且是局部渐近稳定的;若取δ=0.4,则有R1=2.744>1,R2=0.9643<1,根据定理1,地方病平衡点是不存在的.这说明如果因病死亡率δ取值不是太大时(δ=0.2),可以形成地方病.但是,如果因病死亡率δ取值太大时(δ=0.4),则不容易形成地方病,这是由于单位染病者在死亡之前所感染的新得病者不足一个,从而该传染病绝灭.

2 结果与讨论

在定理1的第一种情况下,可以证明平衡点P0是全局渐近稳定的;在第二种情况下,可以证明平衡点P1是全局渐近稳定的;但是对于正平衡点P2的全局稳定性没有证明,这主要是由于时滞的存在,很难找到相应的Lyapunov函数.对于二维系统,可以用Dulac函数判断系统无环,再利用系统的有界性和正平衡点的局部稳定性就可以证明系统正平衡点的全局稳定性.而对于三维系统,目前没有更好的办法来证明正平衡点的全局稳定性.

推论2可以给出生物意义下的解释.若时滞较大(τ>τ0),即如果种群的成熟期较长,种群走向绝灭(平衡点P0是全局稳定的).若时滞较小(τ<τ0),成年种群的密度制约系数很大(β充分大),或者成年种群的出生率和死亡率相差不多(|r-d2| 1),则种群持续生存,疾病消除(平衡点P1是全局稳定的),因为此时Δ<0.只有当时滞取特定值(τ∈(τ3,τ1))时,可以形成地方病.

注意到在推论2的(2)中,还有一种情况没有讨论,即 τ∈ (τ2,τ3).由定理 1 和推论 1 可知,当τ∈(τ2,τ3)时 ,P0和P1是不稳定的,此时P2是否存在,以及P2的稳定性如何,对于这些问题的研究留作以后研究.

3 结 语

本文得出了幼年染病具有阶段结构和时滞的单种群模型中3个平衡点的性质,以及生物意义下的解释,对进一步研究平衡点的稳定性具有一定参考价值.

[1]AIELLO W G,FREEDMAN H I.A time delay model of sing le-species grow th with stage structure[J].M athematics Bioscience,1990,101(1):139-153

[2]AIELLOW G,FREEDMAN H I,WU J.Analysis of amodel representing stage structured populations grow th w ith state-dependent time delay[J].SIAM Journal of App lied Mathematics,1992,52(3):855-869

[3]X IAO Y N,CHEN L S.On an SIS epidem ic model with stage structure[J].Journal of Systems and Science Com p lexity,2003,16(2):275-288

[4]XIAO Y N,CHEN L S.An SISepidemicmodelw ith stage structure and a delay[J].Acta Mathematicae App licatae Sinica(English Series),2002,18(1):607-618

[5]SONG X Y,CHEN L S.Modeling and analysis of a sing le-species system with stage structure and harvesting[J].M athematics and Com puter M odeling,2002,36(1):67-82

[6]SONG X Y,CHEN L S.Op timal harvesting policy and stability for sing le-species grow th model w ith stage structure[J].Journal of Systems and Science Comp lexity,2002,15(2):194-201