四元数映射z→z2+c M集多临界点问题研究

孙媛媛, 王兴元

(大连理工大学信息与通信工程学院,辽宁大连 116024)

0 引 言

20多年来,人们对复映射z→z2+c所构造的M-J集已进行了深入研究[1～3].1982年,Norton发现Julia集不仅仅存在于复数平面,在以四元数为模型的四维空间中同样存在Ju lia集[4].对四元数M-J集的拓扑结构和内部特性的分析逐渐成为一个热点.Gomatam等分析了映射F(Q)+C和CF(Q)下的四元数M集在高维空间的周期稳定性[5];Buchanan等计算并分析了2次、-1次和-2次四元数映射下M集稳定周期域的分布[6];Shizuo分析了四元数M集和Julia集的连通性以及四元数Julia集的拓扑结构[7];M itja等从动力学角度分析了四元数Ju lia集[8];程锦等从理论上分析和证明了指数为正整数的三元数映射的三维广义M集所具有的性质[9];关柯等总结了四元数Julia集的某些特征[10];于海等得到了四维Bannach空间与三维Euclid空间的对应关系[11];Wang等研究了四元数广义M-J集的拓扑结构[12].上述工作丰富了四元数分形理论,但是人们此前对四元数M集的构造多是从单一临界点0开始的.本文将计算四元数映射z→z2+c的M集的临界点集,并讨论临界点不同造成的四元数M集与一般M集的不同特性.

1 实验方法

1.1 四元数M集的临界点集

令四元数z=x0+x1 i+x2 j+x3 k,则f(z)=(x20-x21-x22-x23)+2x0x1 i+2x0x2 j+2x0x3 k+c,其Jacobian行列式可表示如下:

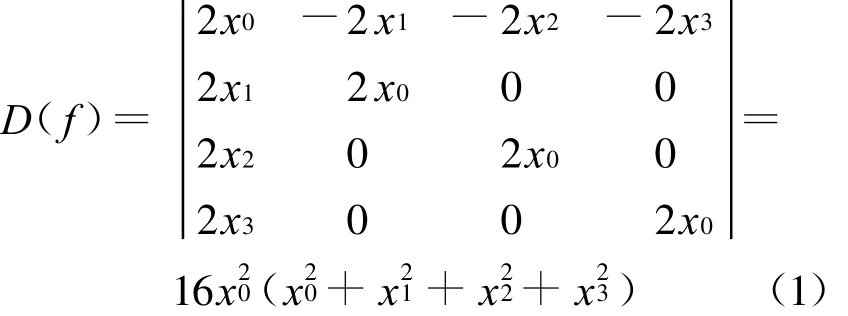
故四元数映射f:z→z2+c的临界点集是平面x0=0上的所有点.

1.2 逃逸时间算法与周期点查找结合法

对于四元数映射f:z→z2+c,取立体网格G(GH)内的点c0,利用逃逸时间算法判断c0是否属于Mf.若c0∈Mf,则判断c0周期性,即求出|fp(c0)-c0|<ε(ε为误差范围,一般ε取10-5)成立的最小正整数p,然后根据p值赋予c0点相应的颜色;若则赋予c0点为黑色.重复上述过程,直到穷尽网格G内所有的点,即可获得M集.

1.3 对逃逸时间算法的一点改进

对于四元数映射f:z→z2+c,取立体网格G(GH)内的点c0,利用逃逸时间算法进行迭代计算.若迭代m次后,|fm(c0)|<δ(δ取0.05,表示小的邻域半径),则根据m的值对点进行相应着色.如果始终未满足上述条件,判断c0是否属于Mf.若c0∈Mf,则赋蓝色 ;若则赋黑色.重复上述过程,直到穷尽视窗W内所有的点,即可获得M集.

1.4 M集上取点构造J集的周期轨道搜索比较法

(1)在Mf上选取p周期点c,令映射f:z→z2+c从z0=c开始迭代,则…,p),可认为ak(k=1,2,…,p)是映射g(z)=fp(z)的不动点.

(2)对立体网格G(GH)内的任意点z,若,可根据k值赋予z点相应的颜色.重复该过程,直到穷尽视窗W内所有的点,即可获得一种新的不同于逃逸时间算法构造的广义J集.

2 多临界点的四元数M集

2.1 四元数M集的性质

在构造不同临界点的M集之前,先给出如下定理.

定理1 四元数映射f:z→z2+c的M集,满足

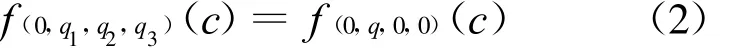
定理2 四元数映射f:z→z2+c的M集,满足

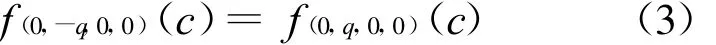
定理2的证明与定理1相同,此处不再赘述.这说明,从临界点z0(0,q1,q2,q3)开始迭代构造的 M 集同构于临界点为z′0(0,q,0,0)(q=的M 集,亦同构于临界点为z″0(0,-q,0,0)的M集.这样在研究四元数M集的拓扑结构时,只要选择适当参数就可研究整个临界点集的M集了.本文中,将临界点为z0(0,q,0,0)的M集映射记为f(q)(c),文中所提的临界点值即指q值.

定理3 四元数映射f:z→z2+c的M集,有

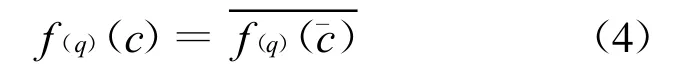
证明 设c=|c|enθ,则c=|c|e-nθ.因为

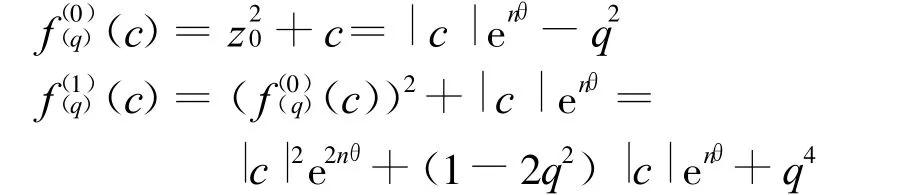
而

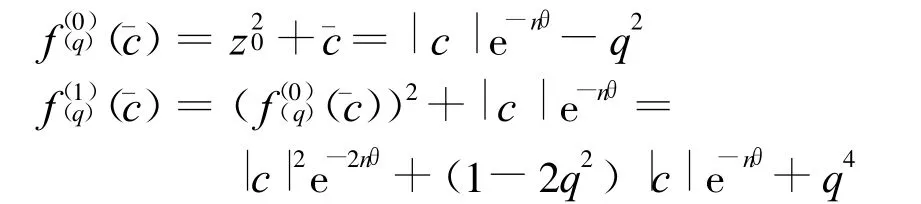
所以

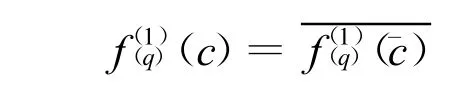
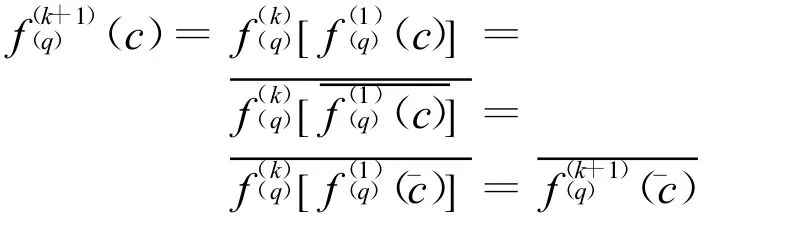
命题真.这解释了为什么不管从哪两个分维观察M集,实验得到的图形均是以实轴为对称的.

定理4[7]四元数映射f:z→z2+c的动力学特征与映射pc0+i|c|:s+it→(s+it)2+c0+i|c|的动力学特征一致.

定理4揭示了四元数M集和复平面M集的关系.同时也说明研究四元数M集的动力学特征及拓扑结构,只要研究与之相对应的二维截面上的M集即可.

图1为q取不同值时,四元数M集在第三、第四分维均为0时得到的二维截面.图中黑色区域为逃逸区,彩色区域通过不同的颜色(由于印刷原因,彩色无法显示)标示了不同周期的稳定区:黄色代表1周期,洋红色代表2周期,红色代表3周期,青色代表4周期,绿色代表5周期,蓝色代表6周期,灰色代表7周期,白色代表8周期…黄色区域为M集的主瓣,是1周期点的集合,主瓣与一系列圆盘形的小花瓣连接在一起,并且每个小花瓣又被一些细节更小的小花瓣所环绕,以至无穷,这体现了明显的分形特征.图1(a)所示四元数M集体现了与复平面M集相同的特征.观察图1(b)～(h),M集在临界点值不为0时,不但体现了上述特征,还表现出差异性.随着临界点值的不断增大,雏瓣和主瓣相继出现了缺失,甚至退化.如图1(b)和放大图(i)所示,q=0.30时,3周期(红色区域)已经出现退化,而2周期(洋红色区域)的变化刚刚开始.图1(c)和(d)中2周期变化更明显.在图1(e)～(h)中,1周期区域不断退化缩小,直至画不出分形图形.根据大量的实验数据得到,稳定区的变化并不是随意进行的,它沿着实轴正向进行.当在正向上变化到一定程度时,再从负向上开始.并且每个花瓣的变化也不是同时发生的,而是从周期较大的花瓣向周期较小的花瓣不断地过渡,直到这种影响波及到最大的花瓣(1周期点区域).

图1 四元数M 集 f(q)(c)(第三、四分维均为0)Fig.1 The quaternion M sets f(q)(c)(the third and fourth dimensions are 0)

2.2 四元数M集的稳定周期域

关于M集f(q)(c)的稳定周期域的边界,假设c=a+iσ·K,t=-q2,那么1周期轨道稳定区域的边界由下式给出:

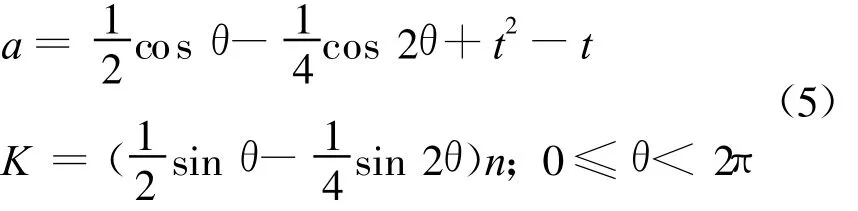
特别地,当t=0时,1周期稳定区的边界为

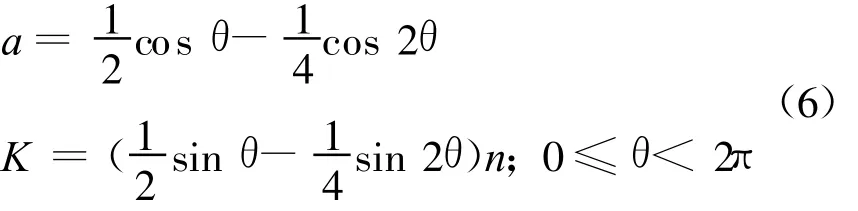
这与复平面M集是一致的,如图1(a)所示的黄色心形区域.

对于其他周期的稳定区的边界,符合下列定理的描述.

定理5 映射f:z→z2+c的p(p>1)周期轨道为z(1),z(2),…,z(p)的稳定区的边界由

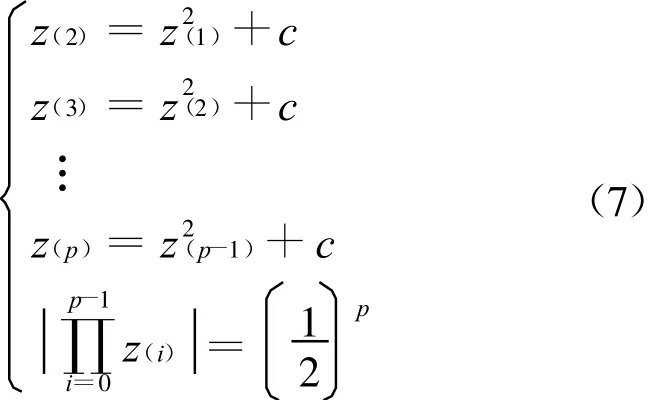
确定.

证明 当p=2时c)2+c,根据p周期轨道的稳定区条件,得到稳定区边界满足.假设当p=n时,边界条件成立,则当p=n+1时,z(n+1)=z2(n)+c,,再由周期轨道的定义,可证定理5成立.

四元数M集f(q)(c)的2周期轨道的边界可由下式给出:

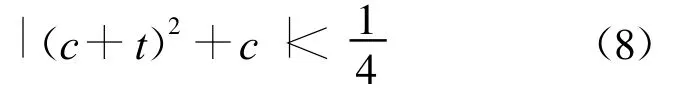
当临界点变化时,四元数M集的区域尽管出现了变化,但是不同周期的稳定区域范围并未变化.变化只体现在区域内部,最为明显的是区域内部的缩小.这说明,对于某点z(z∈H),若z∈f(q)(c),则它的周期值是固定的,并不随着不同的临界点而发生改变.这解释了为什么周期区域变化时,缩小部分的边界并未发现附着更大周期的雏瓣.

Douady等的研究表明,对复平面M集的每个分支花瓣L均有明确的中心,其相反的吸引环是超稳定的,且最多可能有2k-1个分支具有周期为k的吸引子[13].图2所示为采用改进的逃逸时间算法绘制的四元数M集,蓝色区域为稳定区,彩色区域标示了不同周期域中心点的位置,不同颜色代表的周期与图1相同.图2(j)～(l)分别是图2(e)、(f)和(i)竖线标注处的二维虚轴截面.从改进的算法可以看出,图2中彩色部分是不同周期的中心点及其邻域.

图2 改进的逃逸时间算法绘制的四元数M集 f(q)(c)Fig.2 The quaternion M sets f(q)(c)utilizing the improved escape time algorithm

下面计算四元数M集f(q)(c)1～3周期的中心点.

(1)k=1

c-q2=0,1周期的中心在(q2,0,0,0).从图2中可以看出,随着q的不断增大,1周期的中心不断地右移.

(2)k=2

2周期的中心由(c-q2)2+c=0给出,展开此式得到

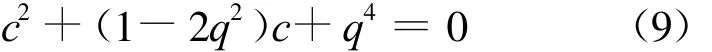
(3)k=3

3周期的中心由((c-q2)2+c)2+c=0给出,展开此式得到

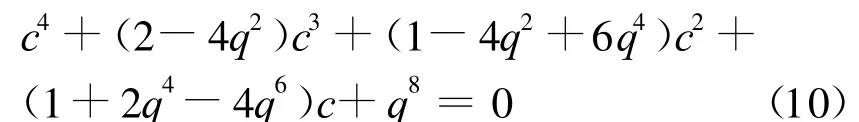
当q=0时,方程3个根为 -1.7549和-0.1226±0.744 9i(抛弃根0).第一个根的位置正好在实轴上2周期区域的左侧,后面两个根的位置在比2周期更靠近实轴的地方.当时,式(10)为该式有4个根,分别为两个实数解-0.实数解0、-0.8042和一对共轭解0.4344±1.007 1i.当q=1时,式(10)为c4-2c3+3c2-c+1=0,该式有两对共轭解,分别为0.,分别0±0.641 2i和0. 2i0±1.227 2i.上述计算说明,随着q的增大,3周期的中心整体在不断沿实轴正向移动.实验结果见图2(a)～(i)的红色区域.

2.3 四元数M集的分岔图

在过去的研究中,一维多次映射x→p(x,u)的混沌或者周期性行为的研究通常采用分岔图作为一种普遍的工具.本文构造的分岔图研究的是四元数映射的实数坐标轴邻域部分,因为它具有较好的图形可视化优点.实验结果表明,四元数映射在实数坐标轴上的投影具有相对于一维二次映射的混沌和周期性行为的图形显示.

从图3中可以看出不同的临界点值对四元数M集混沌或者周期性行为的影响.图3(a)为临界点值为0时的分岔图,此时的图形与一维复数映射是一致的.可以观察到图形具有周期倍分岔现象,这种周期变化先是1周期,然后1周期分岔变为2周期,2周期再分岔变为4周期,逐渐进入到混沌状态.在图3(b)～(d)中也可以明显地看出这种特性.但是同时也看到分岔图随着临界点值的变化而受到了影响.主要表现为分岔图随着临界点值的增大而变窄,某些区域沿着实轴的正方向逐渐地消失.这对应了在2.1节中发现的稳定周期域逐渐消失的现象,并且在实轴上消失的周期域是从较大周期域逐渐波及到较小周期域,这与2.1节的结论也是一致的.如图3(e)和(f)所示,当临界点值大于0.70时四元数M集上的混沌现象已经完全消失了.这主要是因为当临界点值较大时,在实轴上已经无法找到周期为2以上的稳定域了.另外,从分岔图中还可以看到,临界点值非0时周期岔变规律受到一些影响.如图 3(g)和(h)所示,当q=0.40时,从2周期岔变为4周期时产生了振荡.

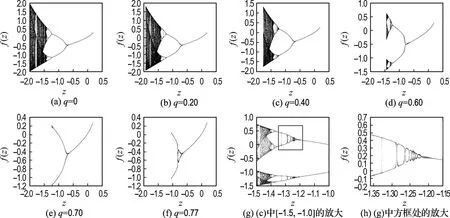
图3 四元数M集的分岔图Fig.3 The bifurcation diagrams of the quaternion M sets

2.4 四元数M集的分形维数

分形是复杂系统,其复杂性可以用非整数维(即分维)描述.分形维数的重要性在于它们能够用数据定义,并且能通过实验手段近似地计算.常见的维数有豪斯道夫维数、盒维数、相似维数、信息维数、关联维数、填充维数、李雅普诺夫维数以及广义维数等.在实际应用中,常用的是盒维数,它能够通过实验近似地计算,并且在一些比较“规则”的集上,这种维数的值与豪斯道夫维数是相等的.

定义1 设集A是度量空间(Rd,ρE)上的有界子集,对每个δ>0,用Nδ(A)表示覆盖A的半径为δ的闭球的最少个数,如果

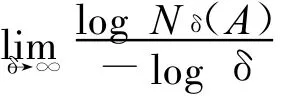
存在,则称这个极限值为集A的盒维数,记为dim BA.

表1为本文计算的部分临界点值情况下M集的盒维数.从表中可以看出,随着临界点值的增大,四元数M集的分维基本上保持着逐步下降的趋势.而当临界点值大于1.0时,M集的维数突然下降很快.从上述计算可以看出,盒维数反映了不同临界点下四元数M集整个周期域的状况.随着临界点值的增大,M集的周期域出现了紧缩,并且M集的边界逐渐模糊,导致很多大周期的稳定域消失,这使得盒维数逐渐降低.而当临界点值大于1.0时,M集的稳定周期域急剧缩小,使得盒维数变化加剧,直至不能产生任何分形结构为止(见图1(g)和(h)).

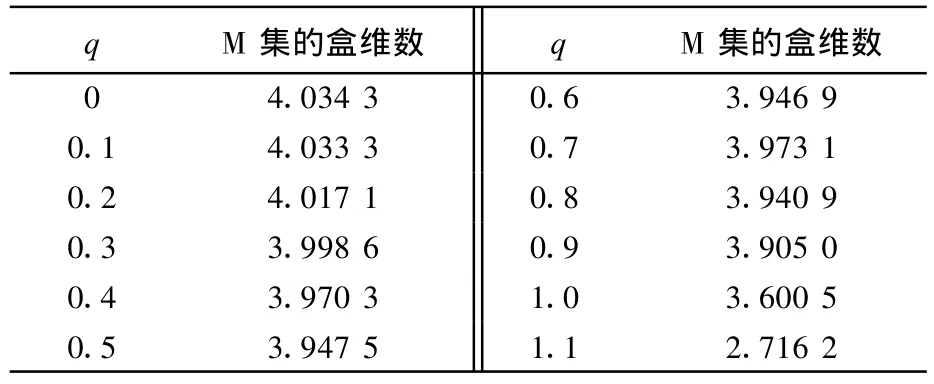
表1 四元数M集的分维Tab.1 Fractal dimensions of the quaternion M sets

3 四元数Julia集

定理6 四元数映射f:z→z2+c的Ju lia集,有

证明 设z=|z|enθ,则

该定理表明四元数Julia集关于原点对称,从图4各图中可以看到这个性质.

图4 四元数Julia集Fig.4 The quaternion Julia sets

定理7 若参数c的标量部分以及范数相同,则四元数Julia集在拓扑结构上保持一致,其迭代后趋向的周期不动点也保持相同范数.

该定理的前半部分是定理4在四元数Julia集中的体现,见图4(i)～(l).尽管它们在实虚两轴的投影看起来不尽相同,实际上这是Julia集旋转了一定角度造成的结果.而在四元数空间中如果参数c遵循定理7中的条件,它们将保持着结构上的一致[12].后半部分结论由本文经过大量的实验发现,示例见表2.由于实验采用的机器计算精度有限,表中数据误差范围在10-4.

Hart等已经证明了当c∈C,j、k存在对称性[14].本文发现这种对称性存在普遍性,将其条件推广得到如下定理.

定理8

(1)若c=|c|eiθ,则对点z(q0,q1,q2,0)和z′(q0,q1,q′2,q′3),如果满足=q′22+q′32,则有|g(z)|=|g(z′)|;

(2)同样的 ,若c=|c|ejθ,则对点z(q0,q1,q2,0)和z′(q0,q′1,q2,q′3),如果满足q21=q′12+q′32,则有|g(z)|=|g(z′)|;

(3)若c=|c|ekθ,则对点z(q0,q1,0,q3)和z′(q0,q′1,q′2,q3),如果满足q21=q′12+q′22,则有|g(z)|=|g(z′)|.

该定理表明如果满足给定的条件,四元数Julia集在某两个虚轴上的投影是圆盘形状.从图4(m)～(p)中可以看到这个性质.

图4给出的是于四元数M集中选点构造的Julia集在任意两个分维平面的投影.如无特别说明,均为另外两个分维为0时的投影.图中黑色表示逃逸区,彩色区域为稳定区,不同的颜色代表趋向不同的周期不动点.在第三、四分维均取0时,图形与复平面 Ju lia集是相同的(见图 4(a)～(e)).而随着第四分维取值的不断增大,分形图形不断收缩,图形面积不断缩小,中间主瓣与周围雏瓣也在不断地融合,整个图形范围越来越小,直至不再产生分形图形(见图4(f)～(h)).这个过程中尽管也出现了图形收缩、扭曲的现象,但是始终保持着关于原点对称的特性,这与定理6是一致的.不同Julia集的周期值和不动点即由参数c在M集中的相应周期域的位置决定(见图4(a)～(h)).本文通过大量实验发现,如果参数c选自任何一个M集,即则对应的Julia 集即为连通的,否则相应的Ju lia集无周期性,无法构造其图像.

表2 四元数Julia集的周期点(3周期)Tab.2 The period point in the quaternion Ju lia sets(3-period)

4 结 论

本文采用逃逸时间算法与周期点查找结合法,构造了四元数映射f:z→z2+c的多临界点M集,探索了多临界点情况下四元数M集的拓扑结构和裂变演化规律,计算了四元数M集的周期域中心位置和边界条件.实验结果表明,不同的临界点会导致周期区域中心发生转移或分化成多个,区域面积也会萎缩或退化,并且萎缩处会出现与周期域特性相一致的分形结构.另外,通过定性地建立M集上点的坐标与Julia集整体结构之间的对应关系,发现四元数M集包含了四元数Julia集构造的大量信息.如果参数c取自由任何一个临界点决定的四元数M集,则相应的Ju lia集即为连通的.这说明四元数映射f:z→z2+c的M集由所有临界点决定的四元数M集的并集组成.可以看出,多临界点的四元数M集结构特点较临界点为0的M集有较大变化,其他映射下的四元数M集亦很有可能存在多临界点问题,下一步工作可再作深入研究.

[1]M ANDELBROT BB.The FractalGeometry of Nature[M].San Francisco:Freeman W H,1982

[2]PEITGEN H O,SAUPE D.The Science of Fractal Images[M].Berlin:Springer-Verlag,1988

[3]王兴元.复杂非线性系统中的混沌[M].北京:电子工业出版社,2003

[4]NORTON A.Generation and display of geometric f ractals in 3-D[J].Computers and Graphics,1982,16(3):61-67

[5]GOM ATAM J,DOYLE J,STEVES B,etal.Generalization o f the Mandelbrot set:quaternionic quad ratic maps[J].Chaos,Solitons and Fractals,1995,5(6):971-986

[6]BUCHANAN W,GOMATAM J,BONNIE S.Generalized M andelbrot sets for meromorphic complex and quaternionic maps[J].International Journal of Bifurcation and Chaos,2002,12(8):1755-1777

[7]SHIZUO N.Dynam ics of a family of quadraticmaps in the quaternion space[J].International Journa l of Bifurcation and Chaos,2005,15(8):2535-2543

[8]M ITJA L,MARJETA S,PETER P.Symbo lic dynam ics in investigation of quaternionic Julia sets[J].Chaos,Solitons and Fractals,2005,24(5):1189-1201

[9]程 锦,谭建荣.基于三元数的三维广义M集表示及其绘制算法[J].计算机学报,2004,27(6):729-735

[10]关 柯,孔凡让,冯志华,等.四元数分形的生成与研究[J].工程图学学报,2005,26(3):133-136

[11]于 海,徐 喆,朱伟勇.单纯形空间中的四元数分形集的构造与分析[J].东北大学学报,2005,26(1):243-246

[12]WANG Xing-yuan,SUN Yuan-yuan.The general quaternionic M-JSetson themappingz→zα+c(α∈N)[J].Computers and Mathematics with Applications,2007,53(11):1718-1732

[13]DOUADY A,HUBBARD JH.On the dynam ics of polynom ial-like mappings[J].Annales Scientifique de l′ cole Normale Superieur,1985,18(4):287-343

[14]HART J C,KAUFFMAN L H,SANDIN D J.Interactive visualization of quaternion Julia sets[C]//Proceedings of the 1st IEEE Con ference on Visualization′90.San Francisco:IEEE Computer Society Press,1990