有限集合上封闭集族的计数*

唐保祥 , 任 韩

(1.天水师范学院数学与统计学院，甘肃 天水 741001；2.华东师范大学数学系，上海 200062)

本文所用术语均是标准的，所用概念或符号均采用文献[1-4]。

有限集合元素的计数问题，在许多实际问题中有重要应用。但是，面对一个具体问题往往很难找到系统和有力的工具来统一解决。因此，解决计数问题往往需要问题解决者创造一些特殊的方法[5-12]，而这些方法又为解决另外一些新问题提供了重要思想。

1 若干定义

定义1 设X是一个集合， 令2X={A|A⊆X}， 称2X为集合X的幂集[1-4]。

定义2 设集合X={a1,a2,a3,…,an},S⊆2X， 若∀A1,A2∈S，A1∩A2,A1∪A2∈S，则称S为X上的一个封闭集族。

对一般的n，具有n个元素的集合X上关于交与并运算封闭的子集族的数目有多少，至今未见有相关结果的文献。本文给出了n个元素的集合上关于集合的交与并运算封闭的部分集族的数目。

2 结果及其证明

设集合X={a1,a2,a3,…,an},本文用f(n,m)表示X上有m个元素的所有不同的封闭集族的数目。对任意正整数n，为了得到m=2,3,4,5时f(n,m)的值，首先给出下面的定理。

定理1 设Z+为正整数集合，∀m,n,i,j,k,l∈Z+，则下面结论成立:

2·3n+1-2n+2+1；

3n+1-2n；

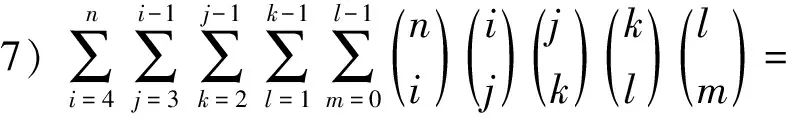
6n-4·5n+6·4n-4·3n+2n。

证明

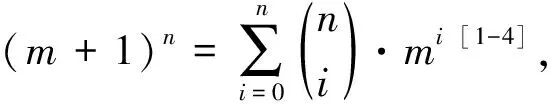
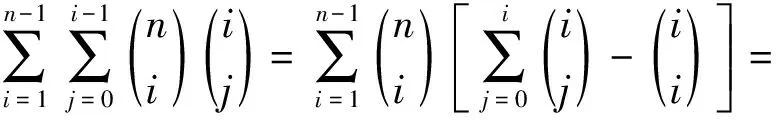
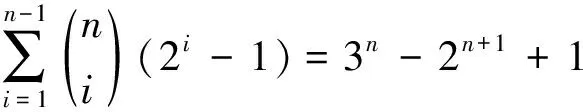
2) 由1)有

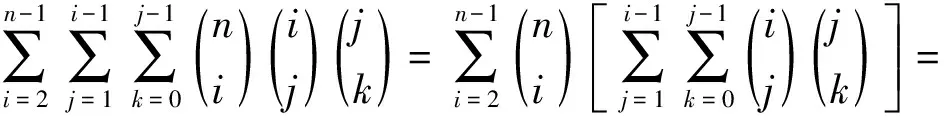
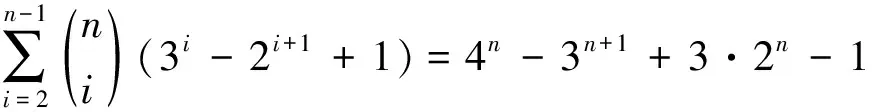
3) 由2)有

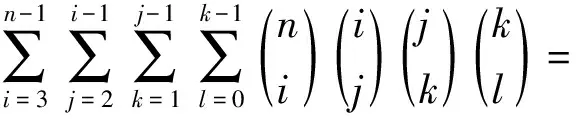
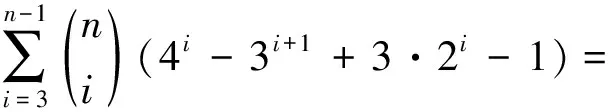
5n-4n+1+2·3n+1-2n+2+1

4)

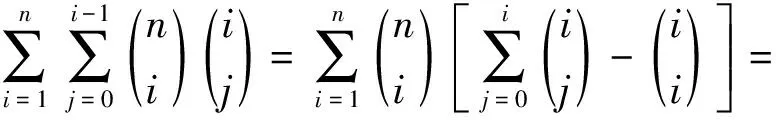
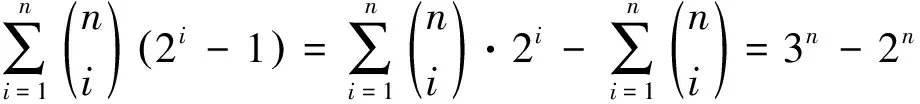
5) 由1)有

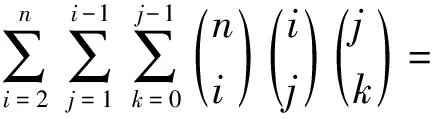
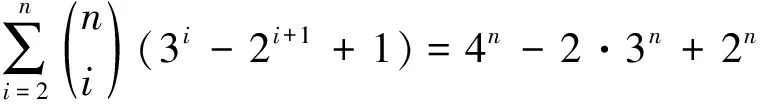
6) 由2)有

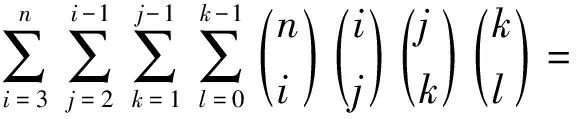
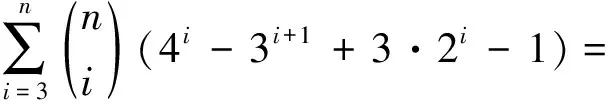
5n-3·4n+3n+1-2n

7) 由3)有

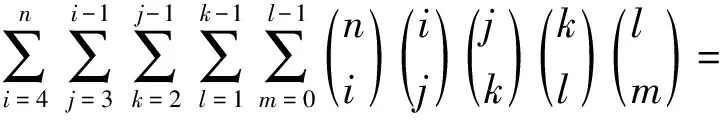
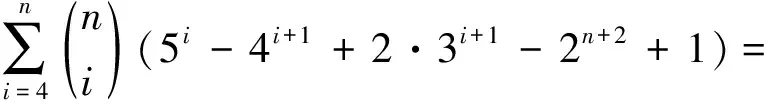
6n-4·5n+6·4n-4·3n+2n

易验证上述7个式子对n≥1的整数都成立。证毕。

定理2 设集合X={a1,a2,a3,…,an}，则

1)f(n,2)=3n-2n；

2)f(n,3)=4n-2·3n+2n；

4)f(n,5)=6n-3·5n+3·4n-3n。

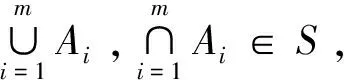
1) 当m=2时，有上述证明可知，A1⊂A2。注意到空集是任何集合的子集，因此

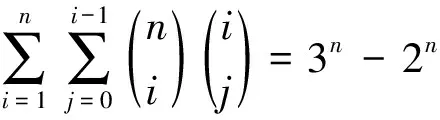
2) 当m=3时，S中的3个元素满足A1⊂A2⊂A3。所以定理1有

3) 当m=4时，S={A1,A2,A3,A4}是X的任一具有4个元素的封闭集族，由上面证明知，A1⊂Ai⊂A4,i=2,3。此时，S分如下两类情形：

(Ⅰ)A1⊂A2⊂A3⊂A4, 或A1⊂A3⊂A2⊂A4；

(Ⅱ)A1=A2∩A3,A4=A2∪A3。

事实上，由于A1⊂A2,A1⊂A3，所以A2∪A3≠A1。

情形1A2∪A3≠A4

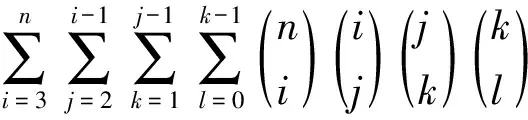
情形2A2∪A3=A4

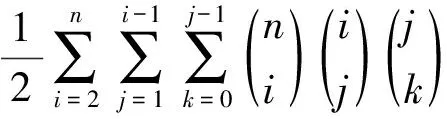
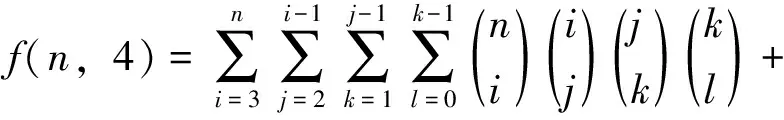
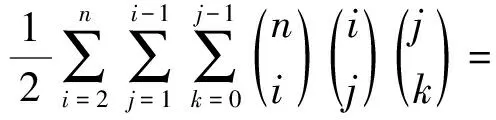
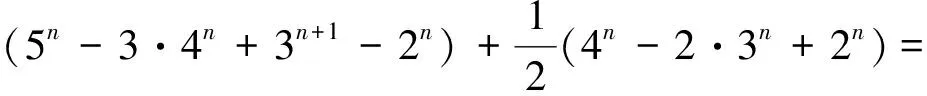
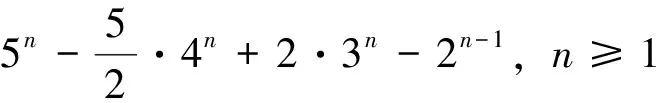
4) 当m=5时，S={A1,A2,A3,A4,A5}是X的任一具有5个元素的封闭集族，由上面证明知，A1⊂Ai⊂A5,i=2,3,4。此时，S分如下三类情形:

(Ⅰ)A1⊂A2⊂A3⊂A4⊂A5, 或A1⊂A3⊂A2⊂A4⊂A5;

(Ⅱ)A1=A2∩A3,A4=A2∪A3,A4⊂A5,A1⊂Ai⊂A5,i=2,3,4;

(Ⅲ)A2∪A4=A5,A3=A2∩A4,A1⊂Ai⊂A5,i=2,3,4。

情形1 ∀Ai,Aj∈{A2,A3,A4}，如果当Ai≠Aj时，总有A1⊂Ai∪Aj⊂A5。因为Ai∪Aj∈S，所以Ai∪Aj∈{A2,A3,A4}。因此，存在Ai,Aj∈{A2,A3,A4},Ai≠Aj，使得Ai⊂Aj。不妨设A3⊂A4。

(i)A2∪A3≠A4

因为A2∪A3≠A4,A2∪A3⊂A5，所以A2∪A3=A2或A3。若A2∪A3=A3, 则由A2⊂A3知,A1⊂A2⊂A3⊂A4⊂A5, 故S是第(Ⅰ)类的。若A2∪A3=A2, 则A3⊂A2。由A3⊂A2,A3⊂A4知，A2∪A4=A2或A4。若A2∪A4=A2, 由A2∪A3=A2知，A3=A4，出现矛盾。 若A2∪A4=A4, 则A2⊂A4。因此，A1⊂A3⊂A2⊂A4⊂A5，故S也第(Ⅰ)类的。

(ii)A2∪A3=A4

若A2∪A3=A4, 则A2∩A3=A1. 事实上，因为A2∩A3=A1或A2或A3。若A2∩A3=A2, 则A2⊂A3, 故A3=A4，矛盾。若A2∩A3=A3, 则A3⊂A2, 于是A2=A4，矛盾。故A2∩A3=A1。因此，S是第(Ⅱ)类的。

情形2 存在不同Ai,Aj∈{A2,A3,A4}，使得Ai∪Aj=A5。不妨设A2∪A4=A5，则A2∩A4≠φ。否则，若A2∩A4=φ, 则{A2,A4}是A5的一个划分。此时，如果A2∩A3≠φ且A3∩A4≠φ，那么A2,A3,A4,A2∩A3,A3∩A4,A5是S中6个互不相同的元素。这与S仅有5个元素矛盾。故当A2∩A4=φ时，A2∩A3=φ, 或A3∩A4=φ。不妨设A2∩A3=φ，则A3⊂A4, 于是A1,A2,A3,A2∪A3,A4,A5是S中6个互不相同的元素。这与S中仅有5个元素矛盾。所以当A2∪A4=A5时，有A2∩A4≠φ。又因A1⊂A2∩A4，故A3=A2∩A4。因此，S是第(Ⅲ)类的。

下面分别计算这三类S的数目。

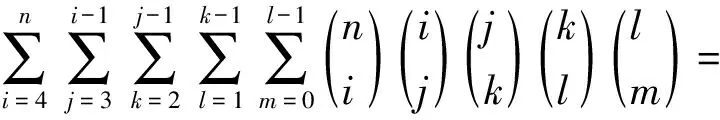
6n-4·5n+6·4n-4·3n+2n

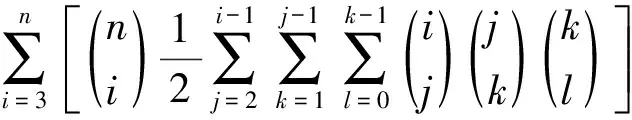
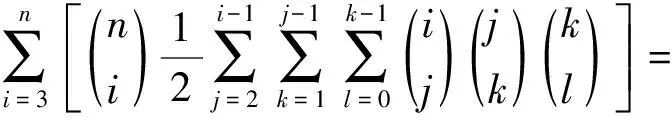
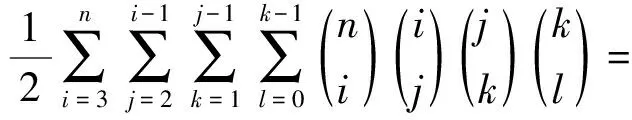
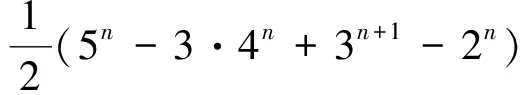
取A5⊆X,A5|=i,3≤i≤n;A2⊂A5,A2|=j,2≤j≤i-1；Y=A5-A2,A3⊂A2,A3|=k,1≤k≤j-1;A4=Y∪A3;A1⊂A3,A1|=l,0≤l≤k-1。于是A2∪A4=A5,A3=A2∩A4,A1⊂Ai⊂A5,i=2,3,4。从而S={A1,A2,A3,A4,A5}是X的第(Ⅲ)类封闭集族。注意到对上述的A2⊂A5,有唯一的A4=Y∪A3。而当A2取A4，A3不变时，对应的A4恰是A2。因此，第(Ⅲ)类封闭集族的数目为

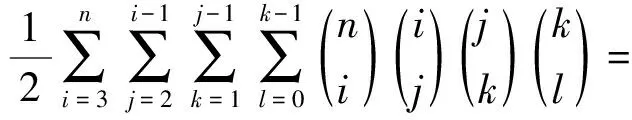
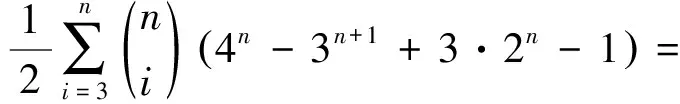
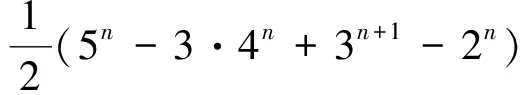
所以

f(n,5)=(6n-4·5n+6·4n-4·3n+2n)+

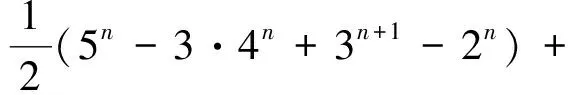
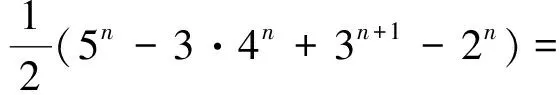
6n-3·5n+3·4n-3n

证毕。

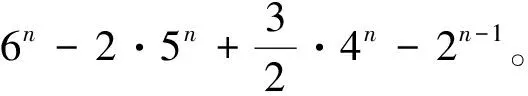
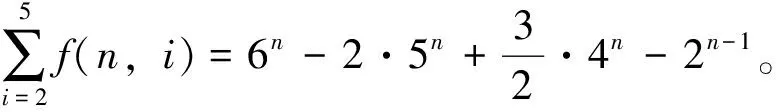
参考文献：

[1] 王元元，王庆瑞，黄纪麟, 等. 组合数学理论与题解[M]. 上海:上海科学技术文献出版社，1989.

[2] 田秋成. 组合数学[M]. 北京:电子工业出版社，2006.

[3] 康庆德. 组合学笔记[M]. 北京:科学出版社，2009.

[4] 王天明. 近代组合学[M]. 大连:大连理工大学出版社，2008.

[5] RICHARD P STANLEY. 计数组合学 [M]. 第一卷.付梅，侯庆虎，辛国策等译.北京:高等教育出版社，2009.

[6] 李磊. 关于几个组合计数公式的推广[J]. 工程数学学报，1996, 13(4):95-98.

[7] 陈宁宇，张武. 不相邻重排列的一种计数方法[J]. 上海大学学报:自然科学版，2005 (1):60-62.

[8] SPRUGNOLI R. Riordan arrays and the Abel-Gould identity [J]. Discrete Mathematics, 1995, 142(1-3): 213-233.

[9] KRATTENTHALER C, MOHANTY S G. Counting Tableaux with row and column bounds [J]. Discrete Mathematics, 1995, 139:237-285.

[10] SU L C, PETER JAU-SHYONG SHIUE. On a combinatorial expression concerning Fermat’s last theorem [J]. Advances in Applied Mathematics, 1997, 18:216-219.

[11] HE T X, HSU L C, SHIUE P J S, et al. A symbolic operator approach to several summation formulas for power series [J]. Journal of Computational and Applied Mathematics, 2005, 177 (1): 17-33.

[12] 龚日朝，廖基定，邹捷中. 一类带约束条件的集合之元素个数计数公式[J]. 应用数学学报，2008, 31(3):385-396.