旋挖钻机变幅机构的动力学建模与仿真

康辉梅，何清华，朱建新

(中南大学 机电工程学院，湖南 长沙，410083)

旋挖钻机是以回转斗、短螺旋钻头或其他作业装置进行干、湿钻进，逐次取土，反复循环作业成孔为基本功能的机械设备。该钻机也可配置长螺旋钻具、套管及其驱动装置，以及地下连续墙抓斗和预制桩桩锤等作业装置[1]。旋挖钻机具有效率高、污染少、功能多等优点，随着我国三峡水电站、青藏铁路、奥运工程、南水北调、西气东输、西电东送、城市地铁轻轨、高速公路等大规模基础工程建设的启动，近年来这种设备在我国得到了广泛应用和发展。目前，国内各大工程机械公司已陆续开始自主研制旋挖钻机。旋挖钻机的结构主要由底盘、回转平台、变幅机构、钻桅、钻杆、动力头和钻具等组成。变幅机构是旋挖钻机一个非常重要的工作装置，由动臂、三角架、连杆及变幅油缸等组成。该机构主要起变幅和支撑作用。变幅功能由两级变幅油缸完成，动臂变幅油缸主要进行钻桅的水平起落及钻孔作业半径的调整，钻桅变幅油缸主要进行钻桅位姿的调整。在整个钻孔过程中，钻具所承受的反作用力和反作用力矩均需通过钻杆和钻桅传递至变幅机构上，再由变幅机构经回转平台和底盘传递至地面。变幅机构的动力学性能对旋挖钻机的主要性能指标如动力头最大输出扭矩有很大影响。而变幅机构的结构形式不同，其动力学性能也不同。目前，人们对旋挖钻机钻桅系统进行了动力学方面的研究[2-3]，而对变幅机构的研究主要集中在构件强度方面[4-11]，并对油缸负载[12]、整机稳定性影响[13]等方面也进行了研究，但对变幅机构进行动力学建模、仿真的研究很少，而对不同形式的变幅机构进行动力学性能的研究则更少。为了研究和改善变幅机构的动力学性能，本文作者采用Simulink软件对变幅机构进行动力学分析、建模和仿真研究。

1 数学模型的建立

旋挖钻机的动臂变幅和钻桅变幅2个动作相互独立进行，本文作者主要研究动臂变幅过程中变幅机构的动力学性能，钻桅分别取水平和垂直2种姿态。动臂在变幅过程中，三角架、钻桅变幅油缸、钻桅、钻杆、动力头、钻具等的相互位置关系保持不变，建模时将这几部分视为1个刚体。动臂变幅油缸所受力简化为方向沿该油缸两铰接点连线的力FN，则动臂变幅机构可以简化为1个承受动臂变幅油缸驱动力和自身重力的四连杆机构。目前，国内外采用平行四边形加小三角结构的变幅机构的旋挖钻机，动臂大都位于连杆上方，但也有一些动臂位于连杆下方的情况；而动臂变幅油缸大都位于动臂下方，即采用上撑的方式，但也有个别动臂变幅油缸安装于动臂上方的情况，即采用上拉的方式。这4种变幅机构的示意图分别如图1所示。下面建立第1种变幅机构形式的数学模型。为了使建立的数学模型具有更广泛的适应性，数学模型采用动臂变幅机构对应的普通四连杆机构，旋挖钻机动臂变幅机构的平行四边形特性在仿真时的参数设定中体现。

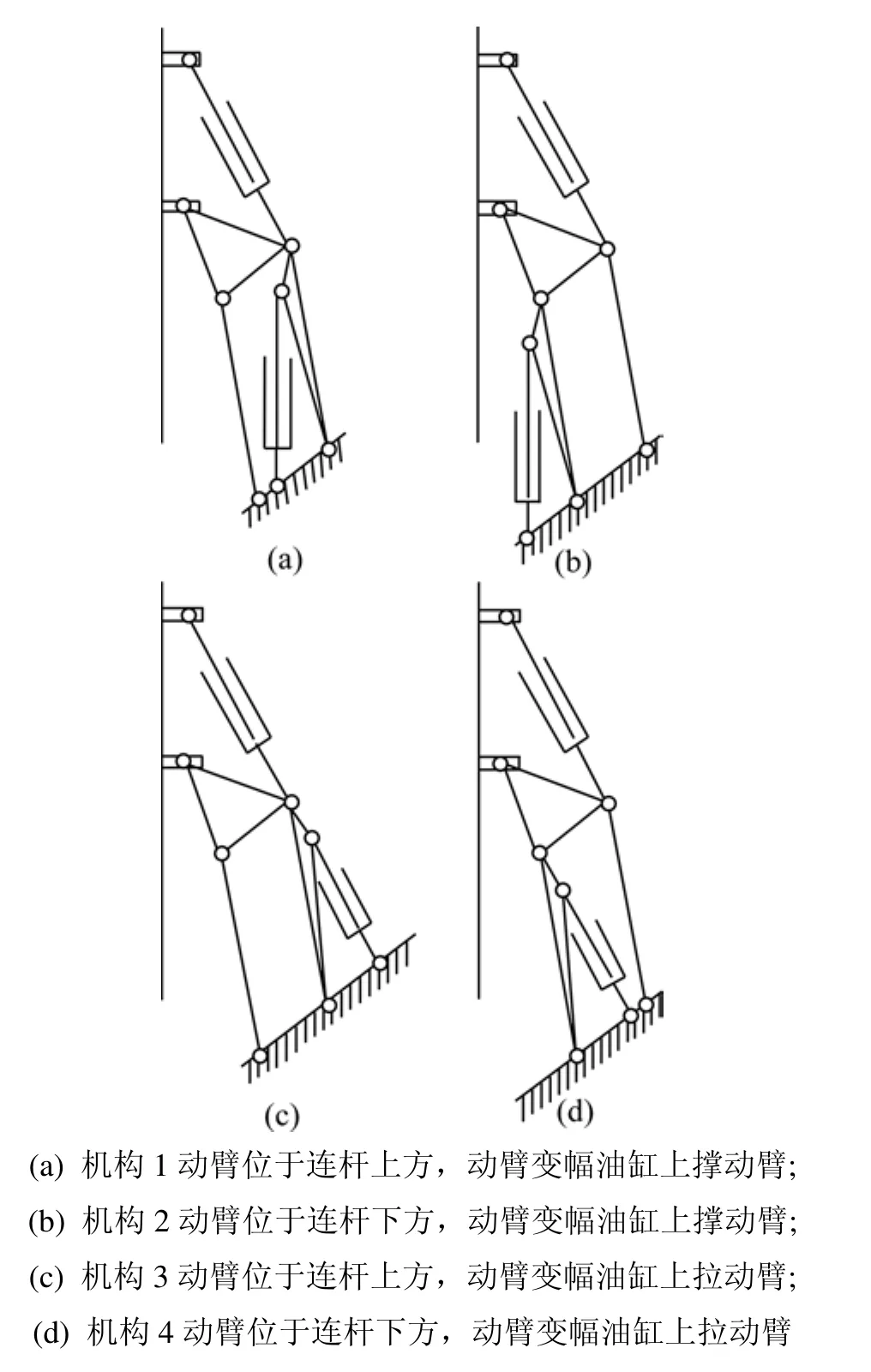
图1 变幅机构的4种形式Fig.1 Four types of mast link frame system

1.1 运动约束方程组的推导

四连杆机构简图如图 2所示，其中：C2，C3和C4点分别为刚体2～4的质心；假设C4点位于CD连线上；α为铰链A和D的连线与水平面间的夹角。四连杆机构闭环ABCD的矢量方程为：

其分量表达式为：

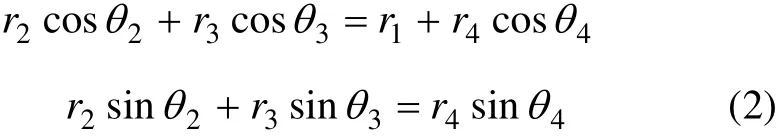
将式(2)对时间求二阶导数，得出加速度方程为：

式(3)表达了由于机构运动约束而产生的各刚体加速度之间的关系。式中：ω2，ω3和 ω4分别为刚体2～4的角速度；ε2，ε3和 ε4分别为刚体 2～4的角加速度。

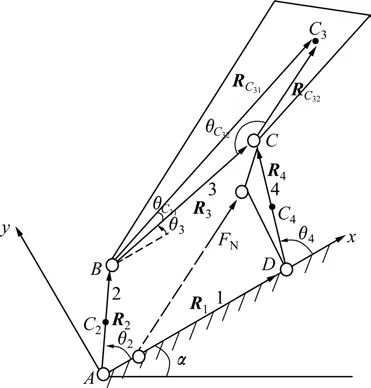
图2 四连杆机构简图Fig.2 Schematic diagram of 4-bar mechanism

下面分别求解刚体 2～4的质心加速度。质心 C2的加速度矢量表达式为：

其标量形式为：

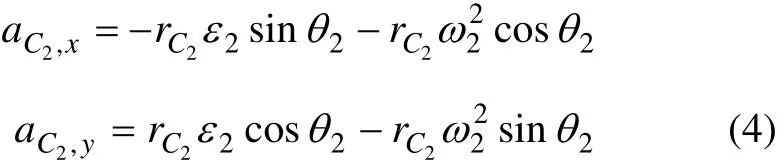
式中：rC2为刚体2质心C2至回转中心A的距离。

质心C3的加速度的矢量表达式为：

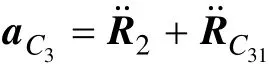
其标量形式为：

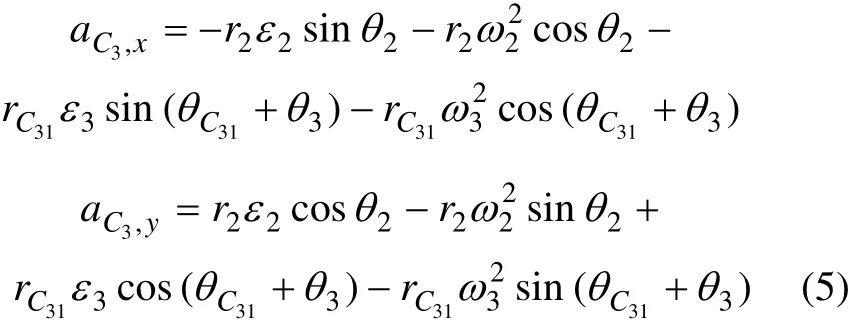
式中：rC31为刚体3的质心C3至回转中心B的距离；θC31为∠C3BC，该角度为常量。

质心C4的加速度的矢量表达式为：

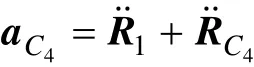
其标量形式为：

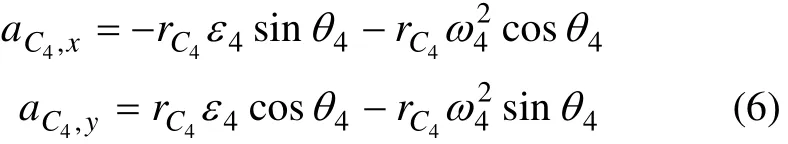
式中：rC4为刚体4的质心C4至回转中心D的距离。

式(4)～(6)将机构的运动学状态和各刚体的质心加速度联系起来。式(3)～(6)共8个方程构成了四连杆机构的运动约束方程组。

1.2 牛顿－欧拉方程组的推导

将四连杆机构的3个运动刚体拆分开来分别进行受力分析(图3)，列写出每个刚体的运动微分方程，从而构成整个机构的牛顿－欧拉方程组。

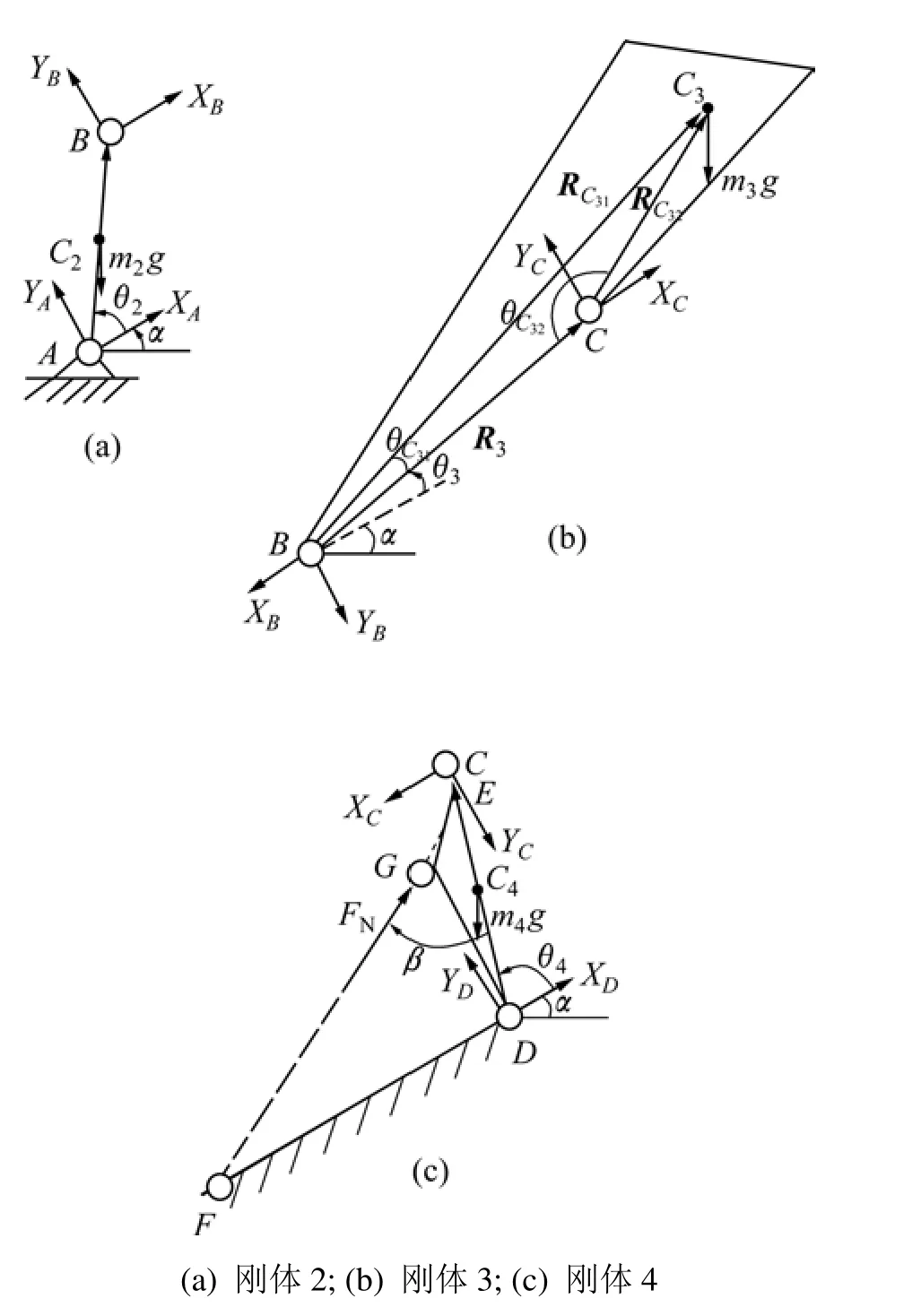
图3 各刚体受力分析图Fig.3 Mechanical analysis of rigid bodies

刚体2绕通过A点的定轴转动，受力简图如图3(a)所示，其运动微分方程为：

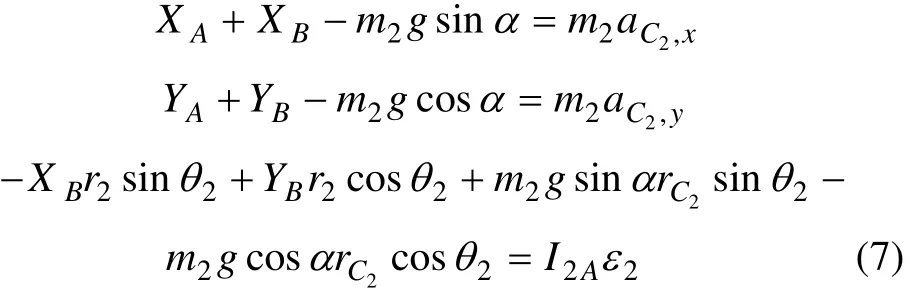
式中：I2A为刚体2绕通过A点的定轴的转动惯量；g为重力加速度，1g=9.8 m/s2。

刚体3做平面运动，受力简图如图3(b)所示，其运动微分方程为：

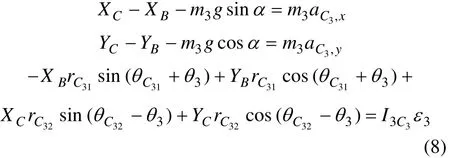
式中：rC32为刚体3的质心C3至回转中心C的距离；θC32为∠C3CB，该角度为常量；I3C3为刚体3绕通过质心C3点的轴的转动惯量。

刚体4绕通过D点的定轴转动，受力简图如图3(c)所示(其中，点E为FG延长线与CD的交点)，其运动微分方程为：

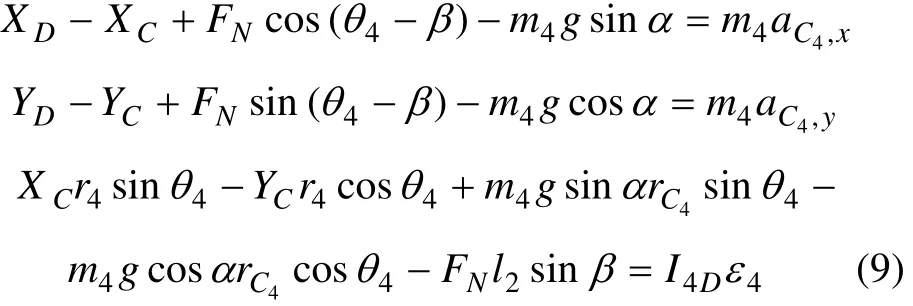
式中：FN为动臂变幅油缸提供的主动力；l1为铰链F和铰链D间的距离；l2为铰链D和点E间的距离，随着动臂的转动，l2会有细微的改变，因不影响后续分析，为了简便，设l2为一定值；I4D为刚体4绕通过D点的定轴的转动惯量。

式(7)～(9)表达了主动力、各刚体间铰链约束反力、运动学状态及各刚体质心加速度之间的关系，共9个方程构成了四连杆机构的牛顿－欧拉方程组。

2 动力学仿真模型的建立

前面已经通过对闭环矢量方程求二阶导数获得 2个表达各刚体加速度间关系的方程，分析各刚体质心加速度而获得6个方程，对每个刚体运用牛顿－欧拉定理导出9个动力学方程，共计17个方程。该四连杆机构共有17个未知数，这17个方程一起构成了一组齐次线性代数方程组。这 17个方程用矩阵形式表示如下：

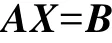
其中：X=[ε2, ε3, FN, aC2,x, aC2,y, aC3,x, aC3,y, aC4,x, aC4,y,XA, YA, XB, YB, XC, YC, XD, YD]T。

A为由X的系数构成的17阶矩阵，B为由各方程已知项构成的列向量。可通过下式求得列向量X：

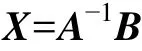
图4 基于Matlab函数的Simulink仿真模型Fig.4 Simulation model based on Matlab function in Simulink

矩阵A是一个17阶矩阵，而且使用Simulink建立动态仿真[14-16]后，每一帧仿真都需要对X进行1次求解，所以，利用Matlab强大的数值计算功能[17]，编写 Matlab函数求解 X。在Simulink平台建立的基于Matlab函数的四连杆机构动力学仿真模型如图 4所示。由外部输入的刚体4的角加速度和分别进行1次积分和2次积分得到的角速度和角度共3项，以及对刚体2和刚体3的角加速度分别进行1次积分和2次积分得到的角速度和角度共4项，这7项表示四连杆机构运动学状态的参数一起构成了 Matlab函数的输入，其他的机构参数在Matlab函数内部定义。Matlab函数的输出包括3部分：第1部分是运动学状态参数，第2部分是四连杆机构各铰链处的约束反力，第3部分是确保公式推导正确无误以及积分过程具有足够精度的相容性校核结果。为了更加便于观察各铰链处约束反力的大小和方向的变化，本仿真中添加了将笛卡尔坐标转化为极坐标的坐标变换模块。

3 动力学仿真和分析

以湖南山河智能机械股份有限公司研制的SWDM－20型旋挖钻机为研究对象，主要的机构参数设定如下：r1，r2，r3和r4分别为1.13，2.74，1.13和2.74 m；l1和l2分别为0.82和3.066 m；m2，m3和m4分别为481，25 115和1 206 kg；α=38˚。

为了增强水平和垂直这2种钻桅位姿状态下变幅机构的动力学性能的可比性，假定主副卷扬安装于钻桅下部。在整个变幅过程中，动臂角加速度的设置如图5所示，仿真时间设为135 s。称动臂和x轴正向的夹角(数学模型中的θ4)为动臂转角，该角度从68˚变化至 144˚。

以上所述为第1种变幅机构形式的动力学数学模型和仿真模型的建立，保持运动参数和所列机构参数等不变，对数学模型、Matlab函数和Simulink仿真模型进行相应修改，即可得出其他3种变幅机构形式的动力学数学模型和仿真模型。

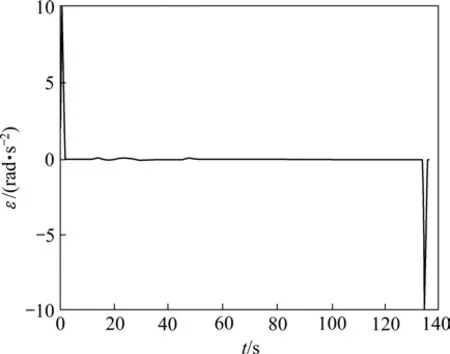
图5 动臂角加速度图Fig.5 Angular acceleration of lift-arm

在整个动臂变幅过程中，变幅机构运动的主动力由动臂变幅油缸提供。4种变幅机构形式在2种钻桅位姿下，在维持机构按图5给定的角加速度曲线运动时，动臂变幅油缸必须提供的主动力随动臂转角的变化关系如图6所示。综合2种钻桅位姿状态下，动臂变幅机构4个铰链处所承受的约束反力中以动臂与转台铰链处所受的约束反力为最大。4种变幅机构形式在变幅过程中，在钻桅水平和垂直时，动臂在其与转台铰链处所受的约束反力 Fdf随动臂转角的变化关系分别如图7和图8所示。鉴于变幅机构所受的力均需通过转台传递至地面，转台所受约束反力的幅值之和Fzf也是1个重要的分析因素，2种钻桅位姿状态下该值随动臂转角的变化关系分别如图9和图10所示。

图6 动臂变幅油缸提供的主动力与动臂转角的关系Fig.6 Relationship between driving forces supplied by hydraulic cylinder of lift-arm and angle of lift-arm

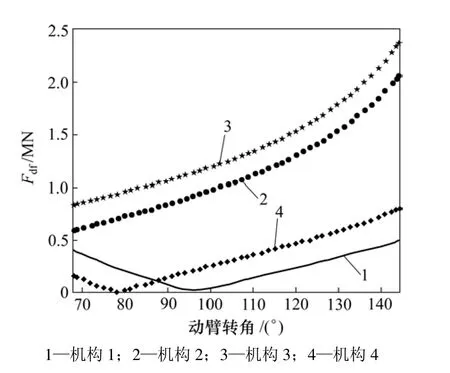
图7 钻桅水平时Fdf与动臂转角的关系Fig.7 Relationship between Fdf and angle of lift-arm when mast is horizontal

由图6可见：整个变幅过程中，随着动臂转角的不断增大，动臂变幅油缸需提供的主动力不断增加；机构1和机构2分别在2种钻桅位姿状态下的4条曲线重合，而机构3和机构4分别在2种钻桅位姿状态下的4条曲线也重合，说明只要运动状态和机构参数等相同，主动力的大小与钻桅的位姿以及动臂和连杆间的相对位置关系无关。从图6还可以看出：机构1和机构2的4条曲线的增速和最大值均明显低于机构3和机构4的4条曲线的对应值，说明动臂变幅油缸和动臂的相对位置关系对动臂变幅油缸需提供的主动力有影响，动臂变幅油缸上撑动臂(机构1、机构2)的性能优于动臂变幅油缸上拉动臂(机构 3、机构 4)的性能。

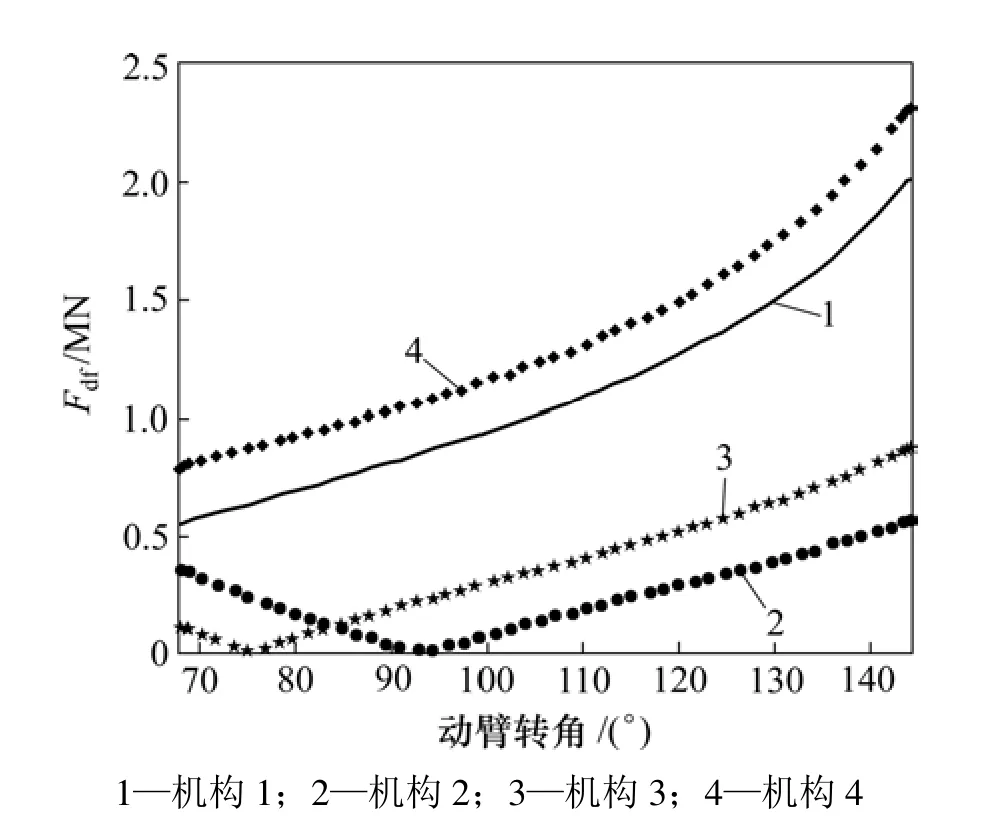
图8 钻桅垂直时Fdf与动臂转角的关系Fig.8 Relationship between Fdf and angle of lift-arm when mast is vertical

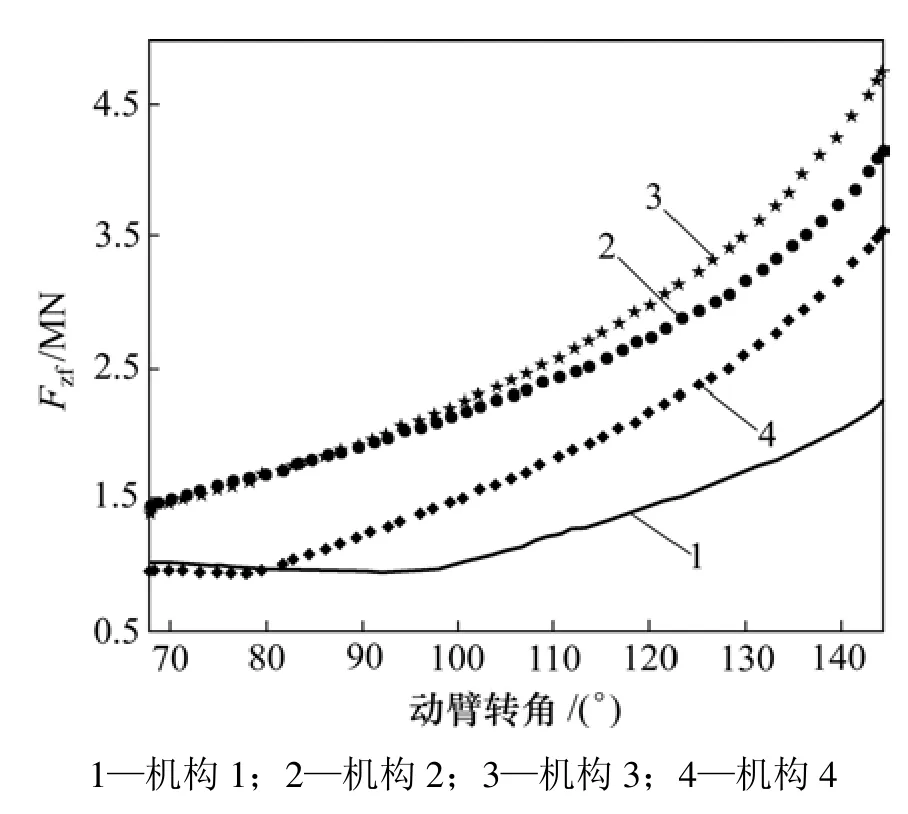
图9 钻桅水平时Fzf与动臂转角的关系Fig.9 Relationship between Fzf and angle of lift-arm when mast is horizontal

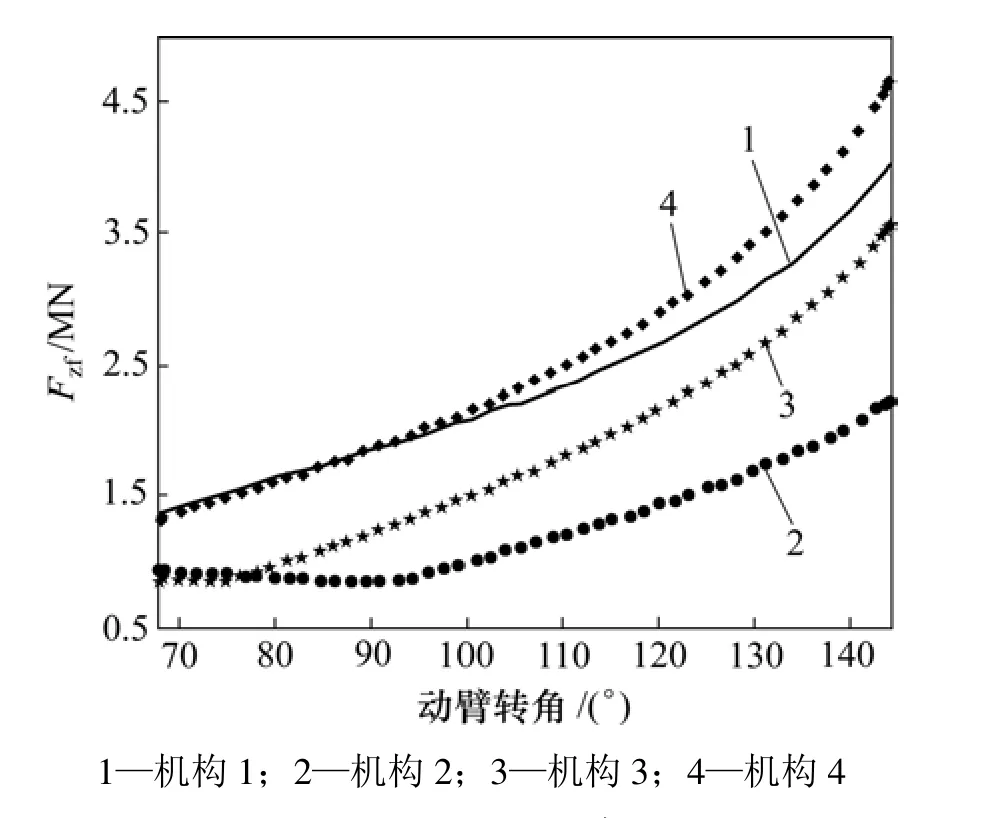
图10 钻桅垂直时Fzf与动臂转角的关系Fig.10 Relationship between Fzf and angle of lift-arm when mast is vertical

图7 表明：对于动臂在其与转台铰链处所受约束反力Fdf，当钻桅位于水平状态时，机构1、机构4、机构2和机构3逐次增大；而图8表明：当钻桅位于垂直状态时，机构2、机构3、机构1和机构4的约束反力逐次增大。对于转台所受约束反力的幅值之和Fzf，通过分析图9和图10中的8条曲线也可以得出同样的结论。这2种不同的变化情况说明：动臂在其与转台铰链处所受约束反力以及转台所受约束反力的幅值之和不仅与变幅机构形式有关，而且与钻桅位姿有关。

考虑到旋挖钻机工作状态下钻桅的位姿主要为垂直状态，再综合考虑不同变幅机构形式对动臂变幅油缸需提供的主动力的影响，变幅机构形式2即动臂位于连杆下方而且动臂变幅油缸上撑动臂的形式能提供比较好的动力学性能。此分析结果对于自主研制适合国内地质条件的高性能旋挖钻机具有重要意义，尤其是进行大扭矩旋挖钻机研制时，采用第2种变幅机构形式可以在很大程度上改善变幅机构的动力学性能。

4 结论

当主副卷扬安装于钻桅下部时：

(1) 在变幅过程中，动臂变幅油缸需提供的主动力的大小与钻桅的位姿以及动臂和连杆间的相对位置无关，和动臂变幅油缸与动臂的相对位置有关；动臂变幅油缸上撑动臂的性能优于动臂变幅油缸上拉动臂的性能。

(2) 对于动臂在其与转台铰链处所受约束反力以及转台所受约束反力的幅值之和，钻桅的位姿状态和变幅机构的形式对其均有影响。

(3) 动臂位于连杆下方而且动臂变幅油缸上撑动臂的形式具有较好的动力学性能。

[1] GB/T 21682—2008, 旋挖钻机[S].GB/T 21682—2008, Rotary drilling rig[S].

[2] 秦四成, 刘晓敏, 王雪莲, 等. NR22型旋挖钻机钻挖系统动力学分析[J]. 筑路机械与施工机械化, 2008, 25(3): 70-72.QIN Si-cheng, LIU Xiao-min, WANG Xue-lian, et al. Dynamic analysis on drilling system of NR22 type rotary drilling rig[J].Road Machinery & Construction Mechanization, 2008, 25(3):70-72.

[3] 杜芳, 李万莉. 旋挖钻机桅杆纠偏控制系统建模与仿真[J].建筑机械化, 2005(7): 30-32.DU Fang, LI Wan-li. Modeling and simulation of rectifying controlling system for mast of thread-type borer[J]. Construction Mechanization, 2005(7): 30-32.

[4] 郭峰, 赵伟民, 胡长胜, 等. 平行四边形起落架有限元计算[J].建筑机械, 2002(8): 37-39.GUO Feng, ZHAO Wei-min, HU Chang-sheng, et al. Finite elements calculation of parallelogram lifting device[J].Construction Machinery, 2002(8): 37-39.

[5] 朱金光, 陈敏革, 刘安宁, 等. 旋挖钻机工作装置有限元分析[J]. 农业装备与车辆工程, 2007(2): 24-27.ZHU Jin-guang, CHEN Min-ge, LIU An-ning, et al. Finite element analysis for the working equipment of drilling rigs[J].Agriculture Equipment & Vehicle Engineering, 2007(2): 24-27.

[6] 何晓艳, 秦四成. 旋挖钻机钻桅三角形连接架的有限元分析[J]. 工程机械, 2007, 38(10): 34-36.HE Xiao-yan, QIN Si-cheng. Finite element analysis for the triangular connecting frame of drill mast on rotary pile drill[J].Construction Machinery and Equipment, 2007, 38(10): 34-36.

[7] 赵伟民, 郭峰, 李瑰贤. SYR200型旋挖钻机桩架整体有限元分析中销轴连接模型的研究[J]. 工程机械, 2005, 36(11):19-22.ZHAO Wei-min, GUO Feng, LI Gui-xian. A study on pin connection model in finite element analysis on complete pile frame of model SYR200 rotary pile drill[J]. Construction Machinery and Equipment, 2005, 36(11): 19-22.

[8] 吴雪梅, 赵伟民, 李瑰贤, 等. 基于有限元方法的钻孔机立柱下铰点结构优化设计[J]. 建筑机械, 2004(6): 80-82.WU Xue-mei, ZHAO Wei-min, LI Gui-xian, et al. Optimization design of hinge joint in drilling machine based on finite element analysis method[J]. Construction Machinery, 2004(6): 80-82.

[9] 赵伟民, 郭峰, 李瑰贤. 基于自由度耦合的旋挖钻机有限元分析中液压缸模型的建立[J]. 工程机械, 2005, 36(12): 36-38.ZHAO Wei-min, GUO Feng, LI Gui-xian. Establishment of hydraulic cylinder model in finite element analysis of rotary pile drill based on degree-of-freedom coupling[J]. Construction Machinery and Equipment, 2005, 36(12): 36-38.

[10] 吴雪梅, 赵伟民, 李瑰贤, 等. 销轴连接的几种有限元模型比较[J]. 机械工程师, 2004(1): 67-68.WU Xue-mei, ZHAO Wei-min, LI Gui-xian, et al. Comparison of finite element models of pin connection[J]. Mechanical Engineer, 2004(1): 67-68.

[11] 杨鹏. X型旋挖钻机的结构分析[D]. 北京: 中国地质大学工程技术学院, 2006: 37-46.YANG Peng. Structure analysis of type-X rotary drilling rigs[D].Beijing: School of Engineering and Technology, China University of Geosciences, 2006: 37-46.

[12] 易炜, 周海生, 赵黎明, 等. 旋挖钻机动臂变幅油缸的负载分析[C]//2006年中国桩工机械行业年会. 长沙, 2006: 31-33.YI Wei, ZHOU Hai-sheng, ZHAO Li-ming, et al. Load analysis of hydraulic cylinder of lift-arm of rotary drilling rig[C]//2006 Annual Conference of China Pile Machinery Industry. Changsha,2006: 31-33.

[13] 赵伟民, 姜文革, 祖海英, 等. 旋挖钻机变幅角度对钻机的影响[J]. 建筑机械化, 2008(6): 36-38.ZHAO Wei-min, JIANG Wen-ge, ZU Hai-ying, et al. Impact of amplitude angle for rotary drilling machine[J]. Construction Mechanization, 2008(6): 36-38.

[14] 约翰·F·加德纳. 机构动态仿真－使用 MATLAB 和Simulink[M]. 周进雄, 张陵. 西安: 西安交通大学出版社,2002.GARDNER J F. Simulations of machines: Using MATLAB and Simulink[M]. ZHOU Jin-xiong, ZHANG Ling. Xi’an: Xi’an Jiaotong University Press, 2002.

[15] ZHANG Ke, WU Yi-xiong, LÜ Xue-qin, et al. Dynamic modeling and simulation for nonholonomic welding mobile robot[J]. Journal of Central South University of Technology,2007, 14(5): 679-685.

[16] 杨英杰, 邓会勇, 李侠. 基于 MATLAB/Simulink的粒度分离过程计算机仿真[J]. 中国有色金属学报, 2006, 16(2): 346-350.YANG Ying-jie, DENG Hui-yong, LI Xia. Simulation of particle separation process based on MATLAB/Simulink[J]. The Chinese Journal of Nonferrous Metals, 2006, 16(2): 346-350.

[17] 张志涌. 精通MATLAB 6.5版教程[M]. 北京: 北京航空航天大学出版社, 2003.ZHANG Zhi-yong. Proficiency in MATLAB, Version 6.5[M].Beijing: Beijing University of Aeronautics and Astronautics Press, 2003.