电铁负荷特性对微机保护启动元件的影响研究
蓝智晖,徐永海
(1.黄岩供电局,浙江 台州 318020;2.华北电力大学电气与电子工程学院,北京 102206)
电铁负荷的冲击特性及其所产生的谐波电流与负序电流,对线路微机保护的不利影响体现在多个方面。目前国内外开展的谐波对继电保护影响的研究较少[1-3],且针对平衡的三相谐波进行,较少考虑电气化铁路谐波单相、具有冲击性,在谐波含量上3次谐波最大,还有较大的5、7次谐波等特点。因此,由三相平衡系统所得出的结论并不能完全适用于电气化铁路谐波问题。
本文根据实际参数,通过电力系统计算机辅助设计(PSCAD)建立地区电网模型与保护常用的三种启动元件模型。对电铁负荷的冲击特性及其所产生的谐波电流与负序电流对线路微机保护启动元件的影响进行了理论分析、仿真验证。
1 微机保护启动元件的特点
微机保护是对数模转换器提供的输入电气量的采样数据进行分析、运算和判断,构成保护的动作特性方程,以实现其保护的功能。其主要元件包括:启动元件、测量元件、时限元件、出口执行元件。启动元件的作用是反应系统故障参数或故障分量,判别系统是否已经发生了故障。正常运行时该元件不启动,整套保护不投入工作,系统发生故障时,其立即使整套保护投入工作。启动元件是微机保护的核心,算法种类较多。以下分别对相电流突变量启动算法、相间电流突变量启动算法及半周电流积分启动算法受电铁负荷特性的影响进行分析。
2 区域电网数字仿真模型的建立
根据某区域电网实际参数,运用PSCAD建立了该电网的数学模型,如图1所示。该区域电网为双电源供电系统,电源为两座220 kV变电站,通过110 kV线路与带有电铁负荷的110 kV变电站联系。依据该电网某时刻的潮流,设置了一般负荷潮流(不含谐波与负序电流)PF1,其有功功率28 MW、无功功率4.3 MW,在仿真过程中始终保持不变;PF2为4台SS6型电力机车负荷,其有功功率18 MW、无功功率8 MW,在仿真过程中0.8 s时投入;F点为线路故障点,仿真过程中设定在5.2 s时线路50%距离处发生A相直接接地短路故障。P点为仿真过程中保护的安装地点,依据某区域电网参数,安装保护处线路的实际额定线电流为400 A,一般启动元件启动整定值为额定电流的20%。

图1 某区域电网接线图
该数字仿真模型在公用电网向电铁牵引变输出的馈线处测得电流波形如图2(a)所示,与实测波形相似,见图2(b)。在图1中P点处测得的仿真电流的基波及2-7次谐波含量如表1所示,同现场实测数据相比,谐波含量较大。
电力机车在行驶过程中,每隔数十公里便会由一座牵引变过渡到另一座牵引变,每座牵引变均由铁道沿线不同的公用变电站供电。也就是说,电力机车的行驶过程会频繁地对铁道沿线公用变电站造成冲击性的影响,机车负荷通常较大,对保护启动元件的影响尤为突出。为了单独分析电铁负荷谐波特性对启动元件的影响,本文设定了一个与电铁负荷功率及功率因数相等的普通负荷(不含谐波电流),在仿真过程中替代电铁负荷,即图1中的PF2,以下简称普通负荷,以便对比观察在没有谐波干扰下的电铁负荷的冲击性,及产生的负序电流对启动元件的影响。

图2 电流波形
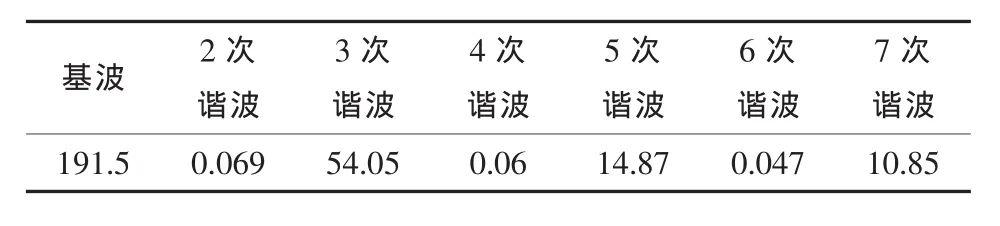
表1 电流谐波含量A
3 电铁负荷对启动元件的影响
保护的故障处理程序在正常时是不启动的,仅在系统故障、启动元件动作后才停止自检,并开始执行故障处理程序。故障处理程序一般比较复杂,不可能在采样间隔时间内完成。而且保护的某些功能也需要启动元件配合,所以启动元件是微机保护必不可少的功能模块。
3.1 对相电流突变量启动算法的影响
保护装置对启动元件的基本要求之一是灵敏度高,因为循环寄存区有一定的存储和记忆容量,可以方便地取得电流的突变量,微机保护通常采用突变量元件启动,突变量Δi(n)为:

式中:i(n)为电流在时刻n的采样值;N为保护在1个工频周期内的采样点数;i(n-N)为比i(n)早1个周期的采样值;Δi(n)为电流在时刻n的突变量。当系统正常运行时,负荷电流是稳定的,或者负荷虽时有变化,但不会在1个工频周期短时间内突然发生很大变化,因此这时i(n)与i(n-N)应接近相等。如果在某一时刻发生短路,故障相电流突然增大,则在n点以后有突变量电流。
图3(a)、(b)分别是电力机车负荷与普通负荷加入公用电网系统时,相电流突变量启动元件所测电流突变量波形图。对比图3(a)、(b)可以看出,在0.8 s时负荷加入公用电网系统,引起承载负荷的A、C两相相电流突变量在2个周波内有较大的波动。只是由于受谐波的影响,图3(a)中电流波形发生畸变,在过零点时刻电流变化率较大,而波峰处变化率较小,近似于梯形波。由式(1)可知,电力机车负荷在波峰处导致图3中0.8 s-0.84 s内相电流突变量测量值最高值没有普通负荷高,而且波形复杂。

图3 相电流突变量启动算法测得的电流突变量测量值
从0.84 s开始,因负荷加入造成的冲击性影响消失,测得普通负荷加入后A、C两相相电流突变量在0~50 A波动。电力机车负荷受谐波影响,且电力系统负荷频率不是恒定不变的值,导致在过零点附近的前一周期采样值与后一周期的采样值差异较大,即式(1)中或差异较大。因而测得电力机车负荷加入后A、C两相相电流突变量在0~80 A波动,变化范围较普通负荷的相电流突变量波动范围(0~50 A)略大。
电力机车负荷、普通负荷加入后发生A相短路故障时电流突变量测量值分别如图3(c)、(d)所示。可见在5.2 s发生A相短路故障后,由于短路电流较大,所得电流突变量测量值受谐波干扰的影响基本可以忽略。
综上所述,相电流突变量启动算法受负荷冲击性影响严重,在负荷加入后的2个周波内波动范围很大,若按该线路实际额定线电流400 A计,启动元件的整定值为80 A,由图3(a)可知,此时启动元件已启动。稳态时(即电力机车加入2个周波后),受谐波影响,所测相电流突变量的变化范围稍大(0~80 A),但其影响有限尚不至于造成保护启动元件误启动。当故障时,由于短路电流较大,测得的电流突变量所受谐波干扰可以忽略,不会造成启动元件的拒动。
3.2 对相间电流突变量启动算法的影响
这种启动方法原理与相电流突变量启动算法类似,只是突变量选取的是相间电流而非相电流,突变量电流的计算一般按式(2)进行:

式中:φφ=AB,BC,CA。
图4是电力机车负荷加入电力系统后的相间电流的波形图,近似于相电流波形。图5(a)、(b)分别是电力机车负荷与普通负荷加入公用电网系统时,相间电流突变量启动元件算法所测电流突变量波形图。对比可知,在0.8 s负荷加入公用电网系统时,都会引起相间电流突变量在2个周波内有较大波动,只是由于谐波的影响(影响原因同相电流突变量启动算法),在0.8-0.84 s内电力机车负荷加入时相间电流突变量最高测量值没有普通负荷高,而且因为A,C两相承载负荷,三相电流不平衡,故AC相间电流突变量值较AB,AC相间电流突变量值高一倍左右。

图4 相间电流波形

图5 相间电流突变量启动算法测得的电流突变量
从0.84 s开始,因负荷加入造成的冲击性影响消失,但是受谐波电流影响(影响原因同相电流突变量启动算法),所测电力机车负荷加入后相间电流突变量波动范围较所测普通负荷加入后的波动范围略大。
电力机车负荷、普通负荷加入后发生A相短路故障时电流突变量测量值分别如图5(c)、(d)所示。可见在5.2 s发生A相短路故障后,由于短路电流较大,AC,AB相电流突变量测量值所受谐波干扰基本可以忽略。
综上所述,相间电流突变量启动算法受负荷冲击性影响较大,在负荷加入后的2个周波内波动范围很大,若按该线路实际额定线电流400 A计算,启动元件的整定值为138 A,由图5(a)可知,此时已经引起启动元件启动。稳态时(电力机车加入2个周波后),受谐波的影响,所测相电流突变量的变化范围稍大(0~80 A),但其影响有限,尚不至于造成保护启动元件误启动。当故障时,由于短路电流较大,测得的电流突变量值所受谐波干扰可以忽略,不会造成启动元件的拒动。
3.3 对半周电流积分启动算法的影响
半周电流积分启动算法的依据是:1个正弦量在任意半个周期内绝对值的积分是1个常数S, 如式(3)所示:

而积分值S可以用梯形法近似求出:

式中:ik为第k次电流采样值;N为1个电流周波的采样次数;i0为k=0时的采样值;iN/2为k=N/2时的采样值。由式4求出积分值S后,可得电流有效值
图6(a)、(b)分别是电力机车与普通负荷加入公用电网系统时,半周电流积分启动元件所测电流突变量波形图。对比可知,在0.8 s即负荷加入公用电网系统后,两种负荷引起电流突变量值的波动都较小。

图6 半周电流积分启动算法测得的电流突变量测量值
由于叠加在基频成份上幅度不大的高频分量在半周期积分中对称的正负半周互相抵消,具有一定的滤除高次谐波的能力,特别是电力机车产生的谐波主要是3、5、7次谐波,因此半周电流积分启动算法所得电流突变量基本不受电力机车产生的谐波影响。
电力机车负荷、普通负荷分别加入后发生A相短路故障时电流突变量测量值如图6(c)、(d)所示。由于半周电流积分启动算法具有一定的滤除高次谐波的能力,所得电流突变量基本不受电力机车所产生的谐波影响。只是半周电流积分启动算法需要的数据窗长度为10 ms,显然较长。
4 RTDS仿真试验
实时数字仿真器 (Real Time Digital Simula-tor,简称RTDS),是一种专门用于研究电力系统电磁暂态现象的装置。由于RTDS模拟器是实时的,因此能被直接连接到电力系统控制和保护装置上。RTDS仿真实验中采用四方公司CSC-103(B)型线路保护装置,其启动元件采用相电流突变量启动算法,测量元件采用解微分方程算法,且测量元件前置了独立的滤波模块。
同PSCAD仿真结果一样,由于电铁负荷的冲击特性及启动定值设置较小,导致线路保护的启动元件频繁启动,只能通过提高启动元件整定值才能避免,但这又严重影响了保护装置的PT断线判别。由于保护装置采用了较好的滤波元件,实验中未发现保护测量元件有误动作,说明线路保护装置若采用滤波效果较好的滤波措施,能够保证保护测量元件的正常工作。
5 结语
通过上述分析可知,相电流突变量启动算法及相间电流突变量启动算法受负荷冲击性影响较大,在负荷加入后的2个周波内波动范围很大,极易引起启动元件的误启动。稳态时(即电力机车加入2个周波以后),受谐波的影响,电力机车负荷加入后相电流突变量和相间电流突变量的变化范围较普通负荷略大,但尚不至于引起启动元件误动作。可见这两种算法在电铁负荷占总负荷比重较大的地区使用时,需将保护启动定值适当放大,以避免电铁负荷冲击性影响。
半周电流积分启动算法所受负荷冲击性影响较小,且具有一定的滤除高次谐波的能力,因电力机车产生的谐波主要是3、5、7次谐波,半周电流积分启动算法所得电流突变量基本不受电力机车所产生的谐波影响。可见该算法虽然灵敏度不如其它两种算法,但应用于电铁负荷占总负荷比重较大的地区时可靠性较好。
[1]张直平.城市电网谐波手册[M].北京:中国电力出版社,2000.
[2]吴竞昌.供电系统谐波[M].北京:中国电力出版社,1998.
[3]胡玉峰,尹项根,陈德树,等.TCSC的继电保护数字仿真研究[J].电力系统自动化,2002.26(16):39-44.
[4]杨奇逊,黄少锋.微型机继电保护基础(第2版)[M].北京∶水利电力出版社,2005.
[5]王梅义.电网继电保护应用[M].北京∶中国电力出版社,1999.
[6]杨奇逊,刘建飞,张涛,等.现代微机保护技术的发展与分析[J].电力设备,2003,4(5)∶10-14.
[7]许正亚.输电线路新型距离保护[M].北京:中国水利水电出版社,2002.
[8]陈皓.微机保护原理及算法仿真[M].北京:中国电力出版社,2007.
[9]郭征,贺家李,杨洪平,等.电力系统故障时继电保护装置动态特性的数字仿真[J].电力系统自动化,2003,27(11)∶38-40.

