一类描述五分Cantor集的拟移位映射
徐园芬, 戴振祥
(1.浙江万里学院 基础学院,浙江 宁波 315101;2.宁波教育学院 信息与艺术学院,浙江 宁波 315010)
0 引 言
1967年,Smale构造了著名的马蹄模型,并成功地运用符号空间上的移位映射刻画了它丰富的动力学性质[1];文献[2]在单边符号空间Σ上引进了一类单边拟移位映射,证明了这类映射是在Li-Yorke意义下混沌的,并且用这类映射描述了Cantor集及平面Cantor集的混沌映射;文献[3]定义了双边符号空间上的一种新的拟移位映射,并证明了它与传统的移位映射σ拓扑共轭,且成功地刻画了Möbius带上一类映射的吸引子的结构及动力学行为.
本文将在单边符号空间Σ3上给出一类单边拟移位映射,证明它在Li-Yorke意义下是混沌的,并用这类映射描述了五分Cantor集的混沌映射.
1 符号空间上的拟移位映射
1.1 拟移位映射的有关定义

空间(Σ3,d)上的单边移位映射σ定义为:对∀s=(s0s1s2…)∈Σ3,σ(s0s1s2…)=(s1s2s3…).现在(Σ3,d)上定义拟移位映射.

1.2 拟移位映射τ的基本结论
定理1(Σ3,τ)与(Σ3,σ)拓扑半共轭.
证明 作映射η:Σ3→Σ3.对于s=(s0s1s2…)∈Σ3,有η(s)=((s0×s1)(s1×s2)(s2×s3)…),易证η在Σ3上连续.
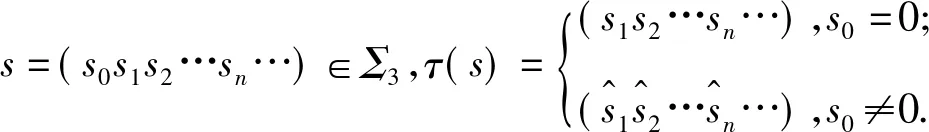
当s0=0时,
η(τ(s))=η(s1s2…sn…)=((s1×s2)(s2×s3)…);
σ(η(s))=σ((s0×s1)(s1×s2)(s2×s3)…)=((s1×s2)(s2×s3)…).
即η∘τ=σ∘η.
当s0≠0时,
σ(η(s))=σ((s0×s1)(s1×s2)(s2×s3)…)=((s1×s2)(s2×s3)…).






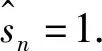
所以η∘τ=σ∘η.因此,(Σ3,τ)与(Σ3,σ)拓扑半共轭.
为了证明τ的Li-Yorke混沌性,首先引进引理1.
引理1[4]若τ是Σ3到自身的连续映射,则τ在Li-Yorke意义下是混沌的充要条件是:存在x,y∈Σ3,使
首先证明τ是连续映射.
定理2拟移位映射τ:Σ3→Σ3是连续映射.
证明 对于∀s=(s0s1s2…sn…)∈Σ3,∀t=(t0t1t2…tn…)∈Σ3,有
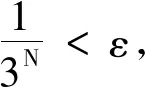
定理3拟移位映射τ在Li-Yorke意义下是混沌的.

k=1,2,…;n=0,1,2,….这样可以得到,对∀r∈(0,1),sr除了k2(k=1,2,…)位置上的符号*不确定外,其他位置上的状态符号都是确定的,且3n位置上对应的状态符号是-1,3n+1位置上对应的是0,3n+2位置上对应的是1,即
作集合S={sr|r∈(0,1)},对∀r1,r2∈(0,1),当r1≠r2时,有ar1≠ar2,故集合S与(0,1)中的实数一一对应,S是一个不可数集.
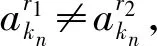
supd(τn(ar1),τn(ar2))≥supd(τkn(ar1),τkn(ar2))>0,


即

2 用拟移位映射描述五分Cantor集的混沌映射
2.1 五分Cantor集I的构造

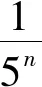
I0⊃I1⊃I2⊃…⊃In-1⊃….
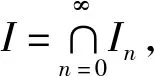
2.2 五分Cantor集I中的点可以用五进制无穷小数表示

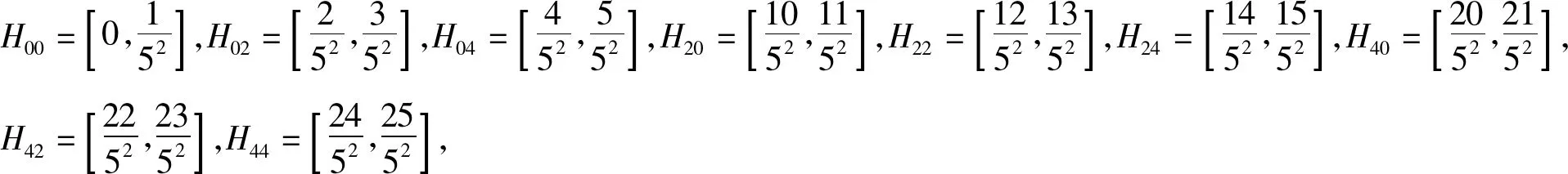
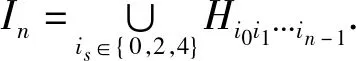
令Hi0i1…in-1=[an,bn],其中an,bn∈I,且an,bn的五进制表示为:an=0.i0i1i2…in-1000…;bn=0.i0i1i2…in-1444…,is∈{0,2,4},s=0,1,2,…,n-1.

由此得到五分Cantor集点的五进制无穷小数表示.
定理4设I为区间[0,1]上的五分Cantor集,∀x∈I,则
x=Hx0x1x2…=0.x0x1x2…,xi∈{0,2,4}.
这样表示的I中的五进制无穷小数中只出现0,2,4,没有1和3.其中:0表示左边区间;2表示中间区间;4表示右边区间.
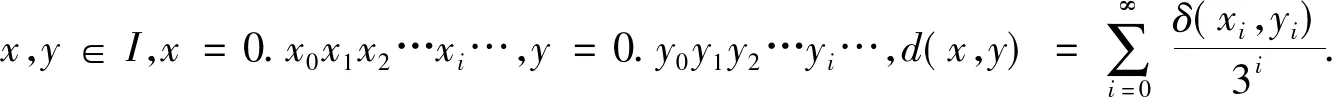
2.3 用拟移位映射描述五分Cantor集的混沌映射
将Σ3={s=(s0s1s2…) |si∈{-1,0,1}}中的符号作如下替换:-1换成0;0换成2;1换成4.则Σ3={s=(s0s1s2…) |si∈{0,2,4}},由此决定了一个由I到Σ3的同胚映射T.
定理5设T是I→Σ3的映射,对∀Hi0i1i2…in-1…∈I,有
T(Hi0i1i2…in-1…)=(i0i1i2…in-1…),(i0i1i2…in-1…)∈Σ3,
则映射T是一同胚映射.

因此T连续.类似可以证明T-1的连续性.故T是一同胚映射.
下面定义I上的拟移位映射.

定理6(I,Φ|I)与(Σ3,τ)拓扑共轭,并且Φ是Li-Yorke意义下的混沌映射.
证明 ∀p=Hi0i1i2…in-1…∈I,有
即τ∘T=T∘Φ.由于T是一一的同胚映射,从而τ与Φ|I拓扑共轭.
由于τ在Li-Yorke意义下是混沌的,从而拟移位映射Φ是Li-Yorke意义下的混沌映射.
致谢:感谢浙江师范大学数理与信息工程学院陈凤娟老师的悉心指导!
参考文献:
[1]Smale S.Differentiable dynamical systems[J].Bull Amer Math Soc,1967,73:747-817.
[2]李明军,李开泰.一类描述混沌符号动力系统[J].高校应用数学学报,1999,14(2):125-129.
[3]陈芳跃,陈凤娟.符号空间的拟移位和Möbius带上的奇怪吸引子[J].应用数学和力学,2003,24(7):747-754.
[4]耿祥义.Li-Yorke混沌的充要条件[J].数学学报,2001,44(5):929-932.

