二阶具变号位势的离散Hamilton系统的周期解*
邓小青
(湖南商学院 信息学院,长沙 410205)
利用临界点理论研究Hamilton系统的次调和解和周期解的存在性,一直是微分方程与差分方程定性理论中的热点问题[1-7],特别地,研究具变号位势的 Hamilton系统的次调和解和周期解也是很重要的课题[1,4].
考虑二阶离散Hamilton系统:
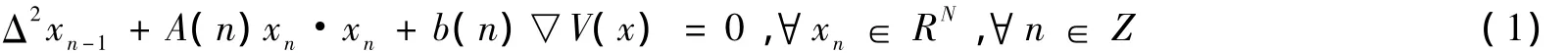
其中b(·),A(·)分别是周期为T(正整数)的实函数和未定的实对称矩阵函数.主要结果为:
定理1 假设b(·),A(·),V(·)≥0满足以下条件:
(V1)V∈C1(RN,R),存在a1>0,a2≥0,β >2,使得V(x)≥a1|x|β-a2,∀x∈RN;
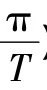
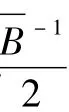
-l2))及r1>0,使得V(x)≤a3|x|2,∀x∈RN,|x|≤r1,其中=max{b
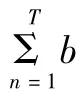
则方程(1)至少有两个非平凡T-周期解.
1 变分结构
N是给定的正整数,对任意给定的正整数T,定义向量空间为ET={x= {xn}:xn+T=xn,xn∈RN,n∈Z}.且ET上的内积和范数分别定义为:
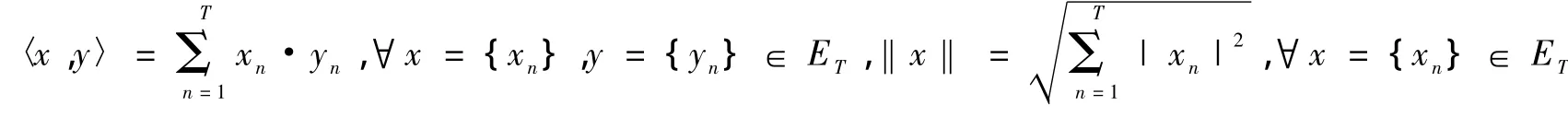
其中xn·yn(n∈Z)表示RN中的内积,表示RN中的范数.
定义线性映射为L:E→RTN为Lx=(x,…,x,x,…,x,…,x,…,x)T,∀x∈E,其中·T表示
T1,1T,11,2T,21,NT,NT向量或矩阵的转置.显然‖x‖=,(ET<·,· >)与RTN是线性同胚的.
在ET上定义泛函F为:
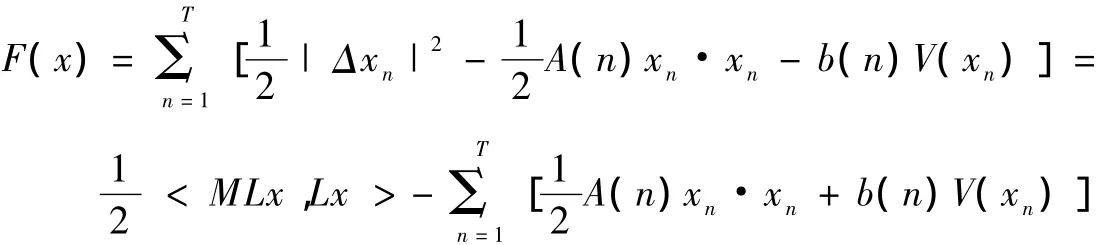
其中M,B见文献[3].易知x∈ET是F的临界点当且仅当x={xn}是(1)的T-周期解.
若令W=KerML={x∈ET:MLx=0}={x∈ET:x={v},v∈RN},则W是ET关于LTML的不变子空间,再令Y是W关于ET的直交补空间,即ET=Y⊕W,则Y也是ET关于LTML的不变子空间.
2 主要结论的证明
引理1 在定理1的假设条件下,泛函F满足P.S.条件.
证明 假设F(x(k))有界及F'(x(k))→0(k→∞),要证{x(k)}在ET存在收敛的子序列,只须证‖x(k)‖有界.F(x(k))有界蕴含存在C>0,使得对任意k∈N有|F(x(k))|≤C.再由条件(V1)和(A)有:

因β>2,式(3)意味着‖x(k)‖有界,因此泛函满足P.S.条件.证毕.
引理2 在定理1的假设条件下,泛函F满足环绕定理[6]的第1个条件.
证明 任意x∈Y及‖x‖≤ρ=>0,由条件(V2)知;
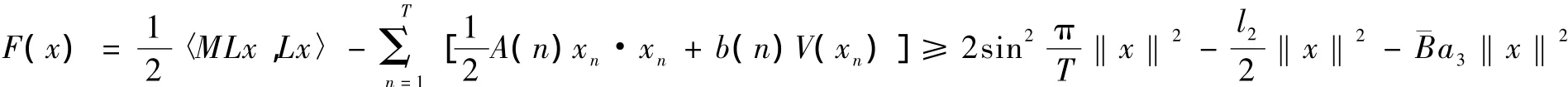
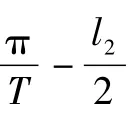

因此泛函F满足环绕定理[6]的第1个条件.证毕.
引理3 在定理1的假设条件下,泛函F满足环绕定理[6]的第2个条件.
证明 显然F(0)=0.选择e∈Y使得en+T=en,∀n∈Z,‖e‖ =1.定义Q(R)=,则∂Q(R)=Q1∪Q2∪Q3,其中Q1={z∈Z:|v|≤R},Q2={re+z:|v|=R,r∈[0},Q3={re+z:|v|≤R,r=
任意z∈Q1,由条件(V1)(A)(B)知:再由Hölder不等式有:
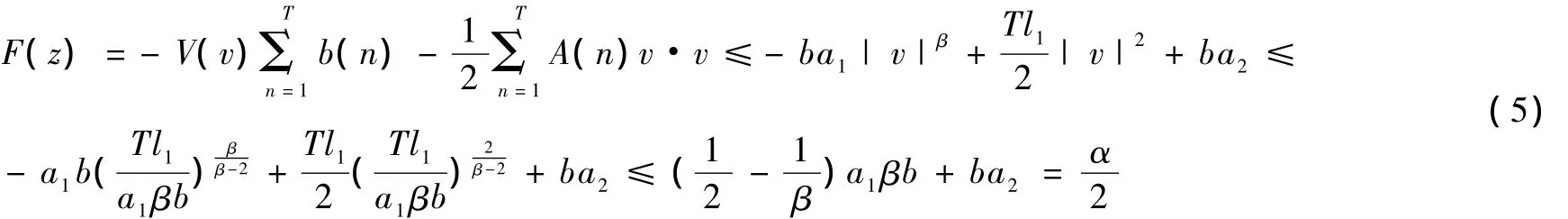
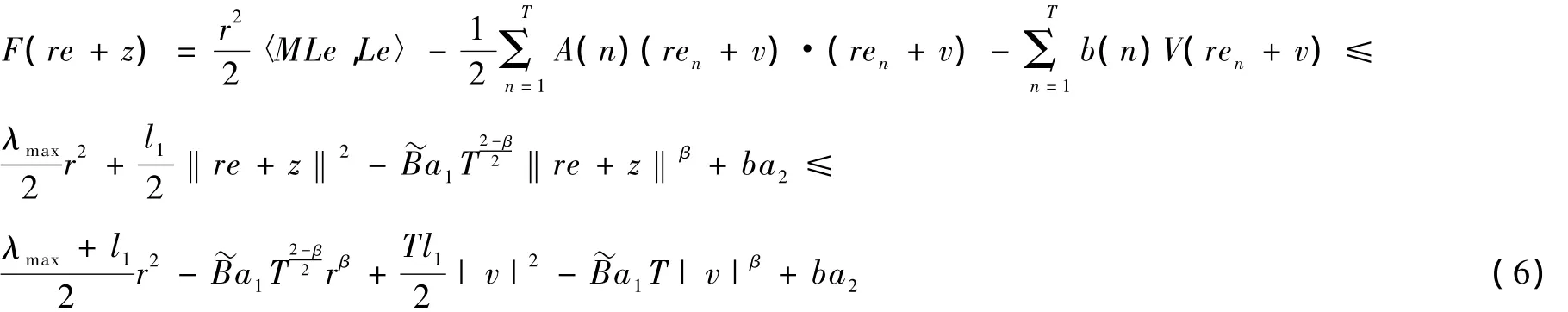
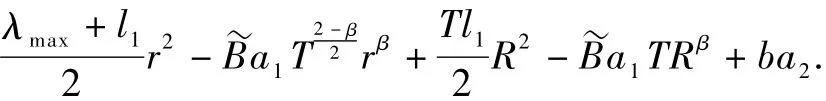
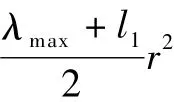
+ba2,假设g'(r0)=0,有g(r)≤g(r0),∀r∈[0,],而且g(r0)是与R无关的常数.于是有F(re+z)≤+g(r0).又因 β>2,所以存在R1>r1使得对任意R>R1,有:

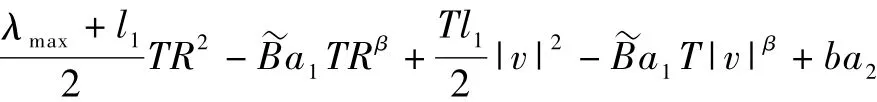

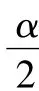
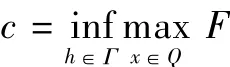
另一方面,类似(3)的证明有:
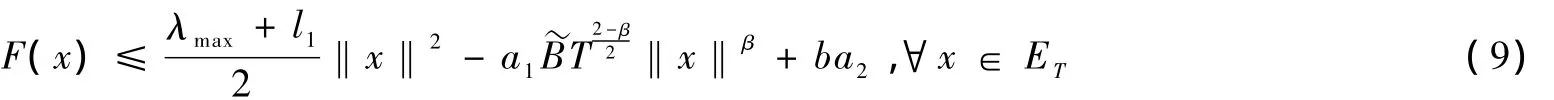
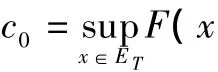
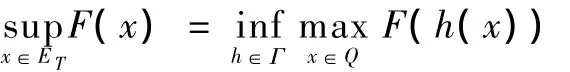
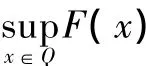
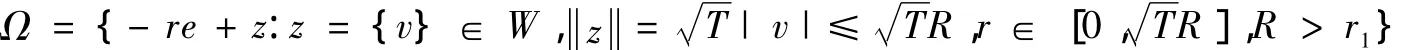
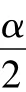
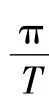
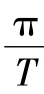
注3 如果定理1及注1与注2中l1=0且a2=0,即A(n)在Z(1,T)上都是半正定或正定的,且V(z)关于z在无穷远点是超二次的,那么去掉条件(B)时,定理1的结论仍然成立.
[1]ANTONACCI F.Existence of periodic solutions of Hamiltonian systems with potential indefinite in sign[J].Nonlinear Analysis,1997,29:1353-1364
[2]GUO Z M,YU J S.Existence of periodic and subharmonic solutions for second-order superlinear difference equations[J].Science in China(Series A),2003,46:506-515
[3]ZHOU Z,YU J S,GUO Z M,et al.Periodic solutions of higher-dimensional discrete systems[J].Proceeding of the Royal Society of Edinburgh,2004,134A:1013-1022
[4]YU J S,DENG X Q,GUO Z M,et al.Periodic solutions of a discrete Hamiltonian system with a change of sign in the potential[J].Journal of Mathematical Analysis and Applications,2006,324:1140-1151
[5]DENG X Q.Periodic Solutions for Subquadratic Discrete Hamiltonian Systems[J].Advances in Difference Equations.2006(2007),16
[6]RABINOWITZ P H.Minimax Methods in Critical Point Theory with Applications to Differential Equations[A].In:CBMS Regional Conference Series in Mathematics Vol.65.Providence[C].RI:American Mathematical Society,1986
[7]王少敏,熊明,茶国智.一类非自治二阶哈密顿系统的周期解的存在性[J].重庆工商大学学报:自然科学版,2008,25(1):5-8

