基于CVaR的投资组合优化模型及实证*

王宝森，梁 奉

(1.北京物资学院 经济学院，北京 101149;2.北京物资学院 研究生部，北京 101149)

现代组合投资决策都是依靠数量化、模型化的方法来确定最优投资组合。根据投资组合优化理论，针对投资者的期望收益率和风险等约束条件，通过对数学模型的求解，给出在风险约束下或者以风险最小化为目标的投资组合有效前沿和资金在各类资产上的投资比例，使投资者可以了解所有的投资机会和各种风险收益状况，然后再根据各自的偏好，在权衡每一个组合后，从中选择满足自己要求的最优投资组合。

关于最优投资组合策略问题，具有奠基性的成果是美国经济学家H.Markowitz提出的经典理论—均值-方差投资组合理论。50多年来，该理论取得了重大进展，如一些学者将风险价值VaR方法引入到投资组合的研究中。Alexander等分析了基于VaR约束的允许卖空情况下的投资组合有效前沿的结构特征。迟国泰等研究了允许卖空情况下基于VaR约束的均值-方差投资组合的有效前沿和最优投资比例。在现有投资组合理论模型中，是以方差来度量风险的。然而，方差并不是一个精确计量风险的度量方法，它既包含人们不愿面对的亏损，又包括人们努力追求的超额回报，并且它也不能确切地指出投资组合损失的可能性到底有多大。因此推出了基于VaR的风险计量模型，以VaR值作为度量风险的大小。

但是当今金融市场错综复杂，资产收益率分布存在尖峰、肥尾等现象。即便收益率分布给定且满足风险价值VaR管理，在极端情况下损失依旧可能很大(即超过VaR的损失值可能是灾难性的)，从而给投资者造成无法接受的灾难性损失。综合考虑以上因素，在合理地估计投资组合收益率下，提出以组合的条件风险价值CVaR为最小目标函数，以组合的VaR为约束条件，通过二次规划的方法，建立投资组合优化模型。这样避免了灾难性的损失，并可以把损失限制在可接受的范围内。

1 模型的设计

VaR方法成为金融市场风险测量的主流方法，但是VaR只适合于在市场正常波动的情况下。由于VaR不满足一致性的要求且在市场在不正常情况下无法估计其损失(特别极端事件下)，而且没有考虑当VaR值被超过时损失究竟是多少的问题，所以当真实损失超过了VaR的度量时，无法进一步识别风险是可以忍受的还是灾难性的。针对VaR的不足，提出了一种VaR的修正方法CVaR，它具有VaR的优点，同时也满足次可加性、凸性等良好的性质。鉴于此，此处试用CVaR来度量风险，仅把VaR作为约束条件。CVaR的简化模型如下:

其中K*即为置信水平取1-c时的VaR，满足P(L≤K*)=1-c;CVaR是指损失超过K*的条件均值，它代表了超额损失的平均水平，反映了损失超过K*时可能遭受的平均潜在的损失大小。

假设超过K*的L值服从标准正态分布L(0，1)，即其密度函数为:

记P(L＜-u1-c)=1-c;则VaR=-u1-c，其中-u1-c为标准正态分布关于c的下侧分位数。

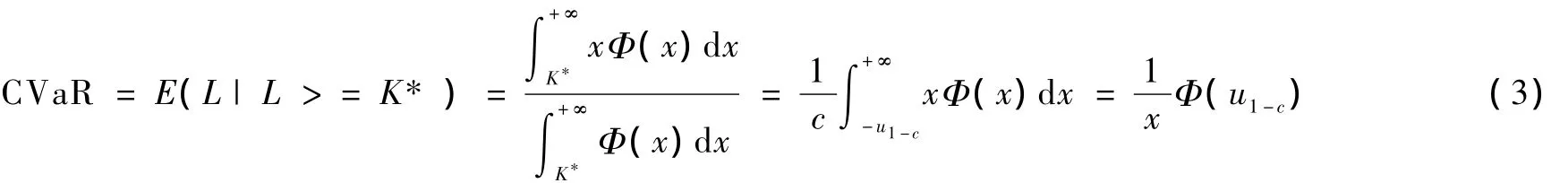
优化的基本原理就是以投资组合的CVaR最小为目标函数，以VaR为约束条件，在合理的区间内选择目标收益率，求解各股票在投资组合中的比重。

2 基于CVaR风险度量和VaR风险约束的贷款组合优化模型

2.1 投资组合确定

假设有n种股票的投资组合，rti为第i只股票在t时的收益率(t=1，2…m;i=1，2…n)。则第i只股票的期望收益为:

假设xi为第i只股票在投资组合中所占的比重。则投资组合的期望收益为:

2.2 目标函数的确定

2.2.1 投资组合方差的确定

利用现有的收益率和收益率数据，可对各项投资组合方差和协方差进行统计估计。，σij(i=1，2，…，n;j=1，2，…，n)分别代表投资组合收益率的方差和协方差的无偏估计:

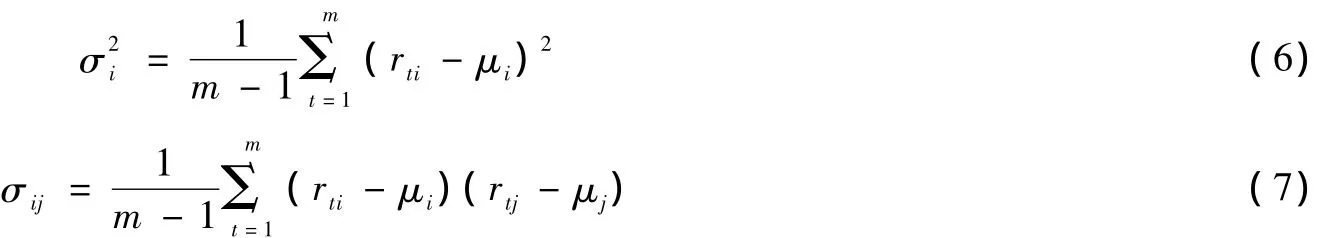
则投资组合的整体风险为:

式中的xi(i=1，2，…，n)为投资组合中第i只股票所占的比重。X=(x1，x2，…，xn)T，U可以用下面式子表示:

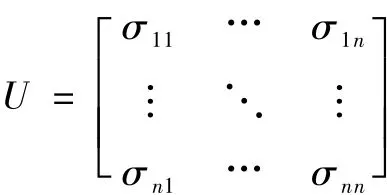
2.2.2 CVaR风险度量的确定

对于投资组合，当有正收益时，意味着无损失;当组合收益为负时，意味着有损失。从而可以定义损失L=-μ。则存在:

若 μi(i=1，2，3，…，n)服从正态分布，则L也服从正态分布，即L～(-μ(X)，σ(X)2)，经过标准化后得出:

根据式(3)和相关数理统计知识可得出:

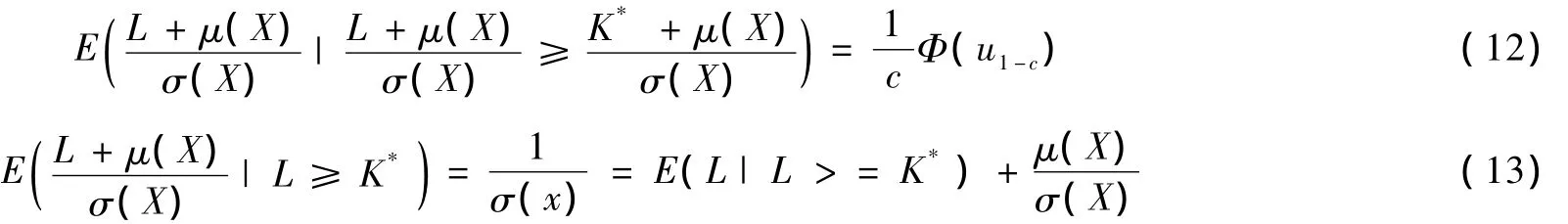
由于式(13)和式(14)两式子的左边相等，从而可得出:

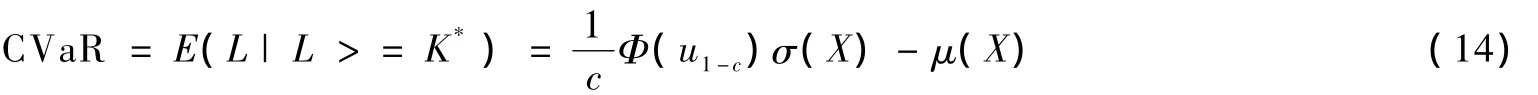
2.2.3 目标函数的建立

将CVaR最小值为投资组合优化目标函数，这样可以降低投资组合发生灾难性风险的可能性。目标函数为:

模型以CVaR最小作为目标函数的好处是反映了损失超过VaR时可能遭受的平均潜在损失的大小。解决了VaR方法无法进一步识别风险是可以忍受的还是灾难的问题，弥补VaR不能反映损失尾部信息的缺失，能防范小概率极端金融风险，降低投资组合发生灾难的可能性。

2.3 基于VaR的组合风险控制

以VaR作为约束条件目的是用组合的VaR收益率最大损失来控制投资组合收益率风险限额，直接反应了风险承受能力。

2.4 模型的建立

目标函数:

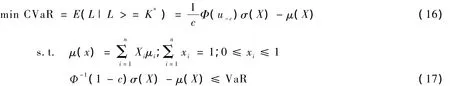
2.5 VaR约束的解释

联立方程(17)和(18)，消除共同项，可以得到CVaR和μ(X)的关系式如下:

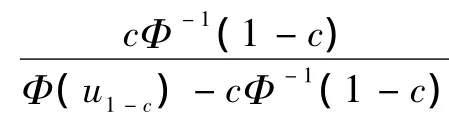
2.6 投资组合收益率合理区间的确定

目标收益率μ(X)应该在模型的有效前沿选取，利用拉格朗日乘子法可以得到有效前沿上最小的CVaR点(图1中的F点)对应的收益率μ(rpm)，其中:

图1 在CVaR～μ(X)空间的VaR约束

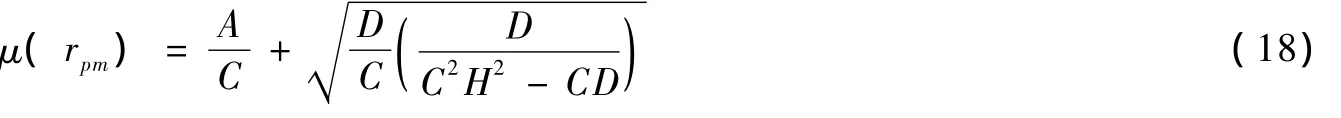
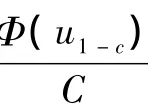
3 实证

3.1 历史数据收集

数据分别取来自不同行业的5只股票，收益率时间段按每天来计算，总共19 d。其收益率的计算为:rti=(PT-PT-1)/pt-1.其中t(t=1，2，…，19;i=1，2，…，5)为天数。根据收集的数据确定组合的收益和方差，并得出收益向量为:R=(R1，R2，R3，R4，R5)=(0.003 7，-0.000 5，0.001 8，0.004 1，-0.00 1)T。其中Ri为第i只股票的平均收益率。

3.2目标函数确定

3.3 VaR约束条件的确定

在限制卖空的情况下，各只股票在投资组合中所占的比例应该大于等于零，即xi≥0(i=1，2，…，5)，且

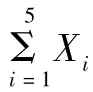
根据其风险承受能力，选定VaR=5%，置信水平1-c=95%，根据正态分布，得出Ф-1(1-c)=1.65，从而有 1.65σ(X)-μ(X)≤0.05。

3.4 投资组合优化模型的建立

综合以上，可得出组合优化模型为:

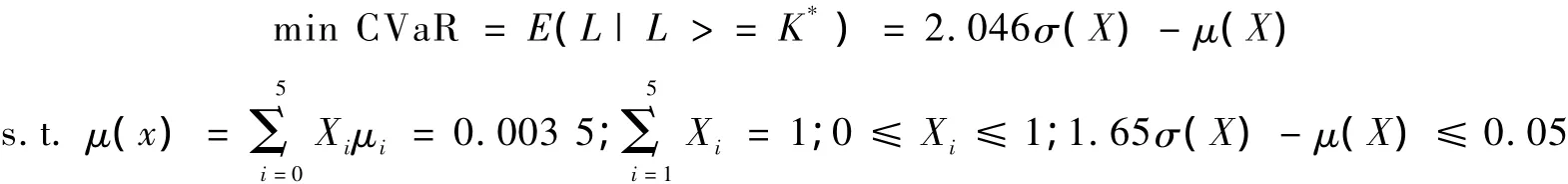
其中σ(X)=

3.5 模型求解及分析

结合Matlab软件和lingo软件求解得出各只股票的投资比例，X=(0.52 0.00 0.17 0.31 0.00)T，最优值即条件风险价值CVaR=0.022 1。各只股票的收益均值、方差及分配比例如表1:

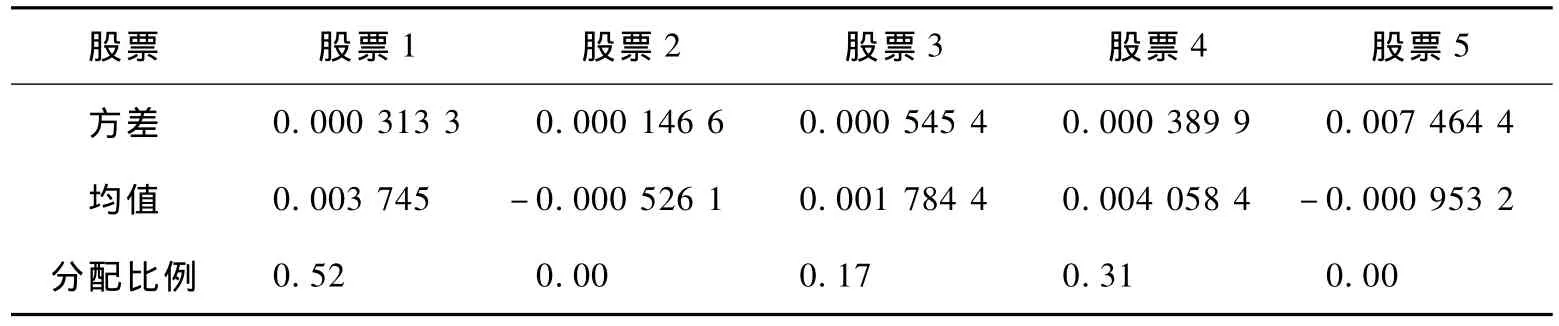
表1 股票的收益均值、方差及分配比例

从表1中分析可以得出:投资组合主要集中于收益率高，方差较小的股票1、股票3、股票4。其中为了保证收益率，投资没有把资金分配于股票2和股票5，同时为了能保证投资组合不发生灾难性风险，投资组合也没有把过多的资金投资于收益率最高但风险较大的股票4，这与经验认识是相符的。

［1］迟国泰，姜大治，奚扬，等.基于VaR收益率约束的贷款组合优化决策模型［J］.中国管理科学，2002(6):2-7

［2］菲利普·乔瑞.风险价值VAR—金融风险管理新标准［M］.陈跃，等译.北京:中信出版社，2005

［3］GOLLINGER T L，MORGAN J B.Calculation of an efficientfrontier for a commercial loan portfolio ［J］.Journal of Portfolio Management，1993，19(2):39-49

［4］ALTMAB E I.Predicting finance distress of companies:revisiting the Z-score and ZETA models［J］.Journal of Finance，2000，55(7):18-20

［5］皮埃特罗·潘泽，维普·K·班塞尔.用VaR度量市场风险［M］.綦相，译.北京:机械工业出版社，2001

［6］刘次华，万建平.概率论与数理统计［M］.北京:高等教育出版社，2003

［7］林旭东，巩前锦.正态条件下均值CVaR有效前沿的研究［J］.管理科学，2004(6):52-55

［8］迟国泰，王际科.基于CVaR风险度量和VaR风险控制的贷款组合优化模型［J］.预测，2009(2):47-52

［9］何琳洁，文凤华，马超群.基于一致性风险价值的投资组合优化模型研究［J］.湖南大学学报，2006，53(1):67-70

［10］CAMPBELL R，HUI SMAN R，KOEDIJK K.Optimal portfolio selection in a Value—at—Risk framework［J］.Journal of Banking ＆ Finance，2001，25:1789-1804