一类具有常数收获率的具有功能性反应捕食模型的定性分析

倪春青，胡志兴

(北京科技大学 应用科学学院，北京 100083)

关于具有Holling功能性反应的捕食者-食饵模型，目前已有不少研究结果.文献［1-3］研究了一类具有HollingⅢ功能性反应的食饵捕食-被捕食模型的极限环，证明了在一定条件下，正平衡点外围存在唯一稳定的极限环.文献［4］研究了一类被开发的捕食-食饲系统，证明了不稳定的平衡点附近存在唯一极限环.文献［5］研究了一类具有HollingⅣ类功能反应的捕食-食饵模型，得到了系统轨线的全局稳定性、极限环的存在性及系统无环的一些充分条件.文献［6］和文献［7］研究了一类具有功能反应的食饵捕食者系统模型，得出平衡点的性态，极限环不存在的判定条件.

1 模型的平衡点及其性态

考虑食饵种群在一类密度制约条件下，两种群均具有收获率的功能反应模型:

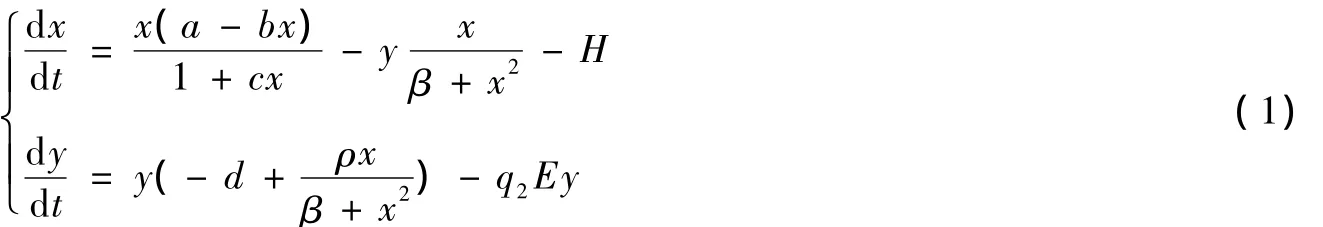
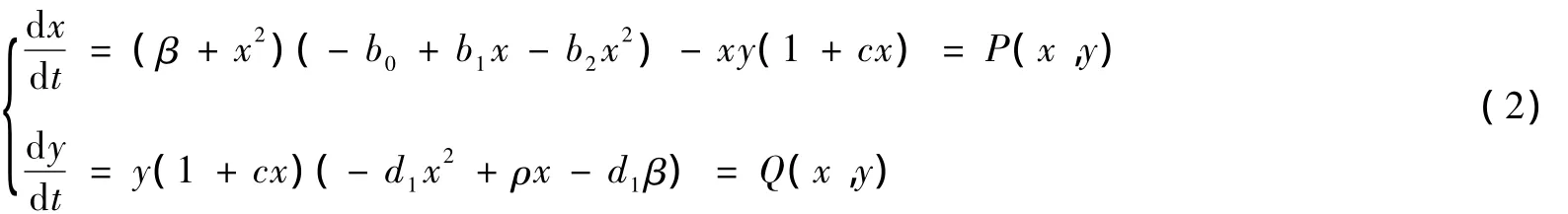
其中b0=H，b1=a-Hc，b2=b，d1=d+q2E.

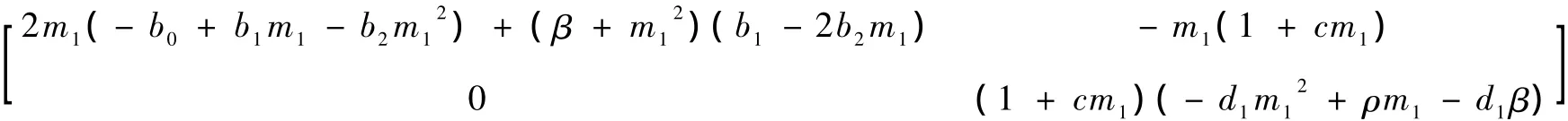
所以系数矩阵的行列式D=(β+)(b1-2b2m1)(1+cm1)(-d1+ ρm1-d1β).

定理1 1)在x2＞m1＞x1的条件下，b1-2b2m1＞0时，平衡点M1(m1，0)为模型(2)的不稳定结点.b1-2b2m1＜0时，平衡点M1(m1，0)为模型(2)的鞍点;

2)在x1＞m1的条件下，b1-2b2m1＞0时，平衡点M1(m1，0)为模型(2)的鞍点.b1-2b2m1＜0时，平衡点M1(m1，0)为模型(2)的稳定结点;

3)在m1＞x2的条件下，b1-2b2m1＞0时，平衡点M1(m1，0)为模型(2)的鞍点.b1-2b2m1＜0时，平衡点M1(m1，0)为模型(2)的稳定结点.

上述结论对M2(m2，0)也成立.

证明 1)x2＞m1＞x1，b1-2b2m1＞0时，-+ ρm1-d1β ＞ 0，＞0，迹T=2m1(-b0+b1m1-b2m1

2)+(β+)(b1-2b2m1)+(1+cm1)(-+ ρm1-d1β)＞0.所以x2＞m1＞x1，b1-2b2m1＞0时，＞0，T＞0，平衡点M1(m1，0)为模型(2)的不稳定结点.x2＞m1＞x1，b1-2b2m1＜0时，＜0，平衡点M1(m1，0)为模型(2)的鞍点;

2)x1＞m1，b1-2b2m1＞0时，-+ ρm1-d1β ＜ 0，＜0，平衡点M1(m1，0)为模型(2)的鞍点.x1＞m1，b1-2b2m1＜0时，＞0，T＜0，平衡点M1(m1，0)为模型(2)的稳定结点;

3)m1＞x2，b1-2b2m1＞0时，-+ ρm1-d1β ＜ 0，＜0，平衡点M1(m1，0)为模型(2)的鞍点.m1＞x2，b1-2b2m1＜0时， ＞0，T＜0.平衡点M1(m1，0)为模型(2)的稳定结点.

同理可得M2(m2，0)的上述类似结论.

定理 2 当m1＜x1＜m2，b1-2b2x1＜0，-2βcx1-β ＜ 0时，T＜0，R1(x1)为稳定的焦点或结点.当b1-2b2x1＞0，-2βcx1-β ＞ 0时，T＞0，R1(x1)为不稳定的焦点或结点.R2()为模型(2)的鞍点.

证明 由模型(2)知，正平衡点R1(x1)处的系数矩阵为:

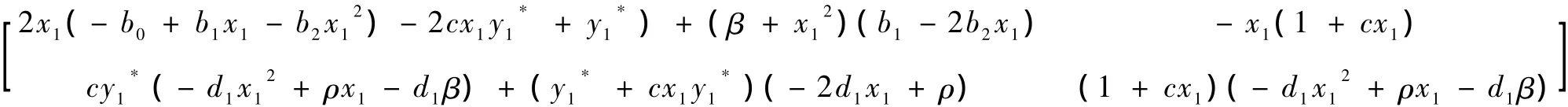
其中l1=2x1(-b0+b1x1-)-(+)+(β+)(b1-2b2x1)，l2=-x1(1+cx1)，l3=(+)(-2dx1+ρ).系数矩阵的行列D=-l2l3=(1+cx1)(1+cx1)(-2d1x1+ρ)=x1

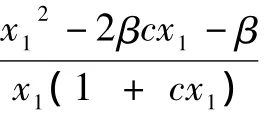
2 极限环的不存在性

定理3 若正平衡点R1(x1，)稳定，且满足 3b1＜d1，ρ＜d1βc+2b0+2βb2，则模型(2)无极限环，轨线趋于R1(x1).正平衡点R1(x1)不稳定，且满足 3b1＜d1，ρ＜d1βc+2b0+2βb2，则模型(2)无极限环.

证明 若存在极限环，则必围绕正平衡点R1(x1)，取 Dulac 函数B(x，y)=xrys，

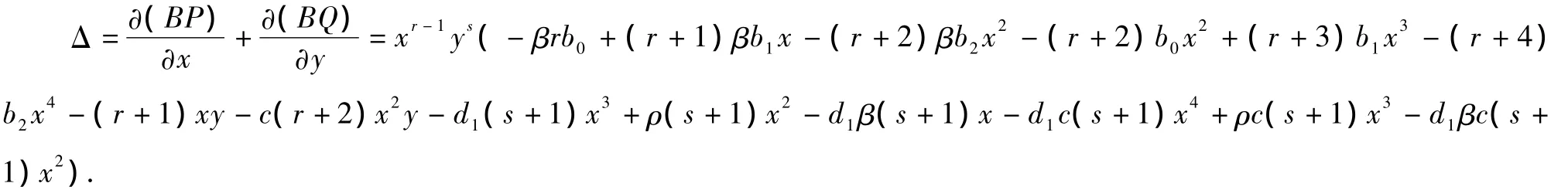
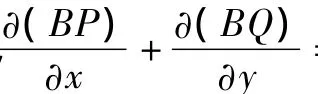
3 数值仿真与生态意义

在定理3的条件下，取合适的参数，运用Matlab绘图程序，得到系统不存在极限环的图形.图1显示在相应参数下，两种群共生共存，最终保持在平衡位置R1(x1).图2显示捕食者最终趋于灭亡.

图1 平衡点稳定时模型不存在极限环

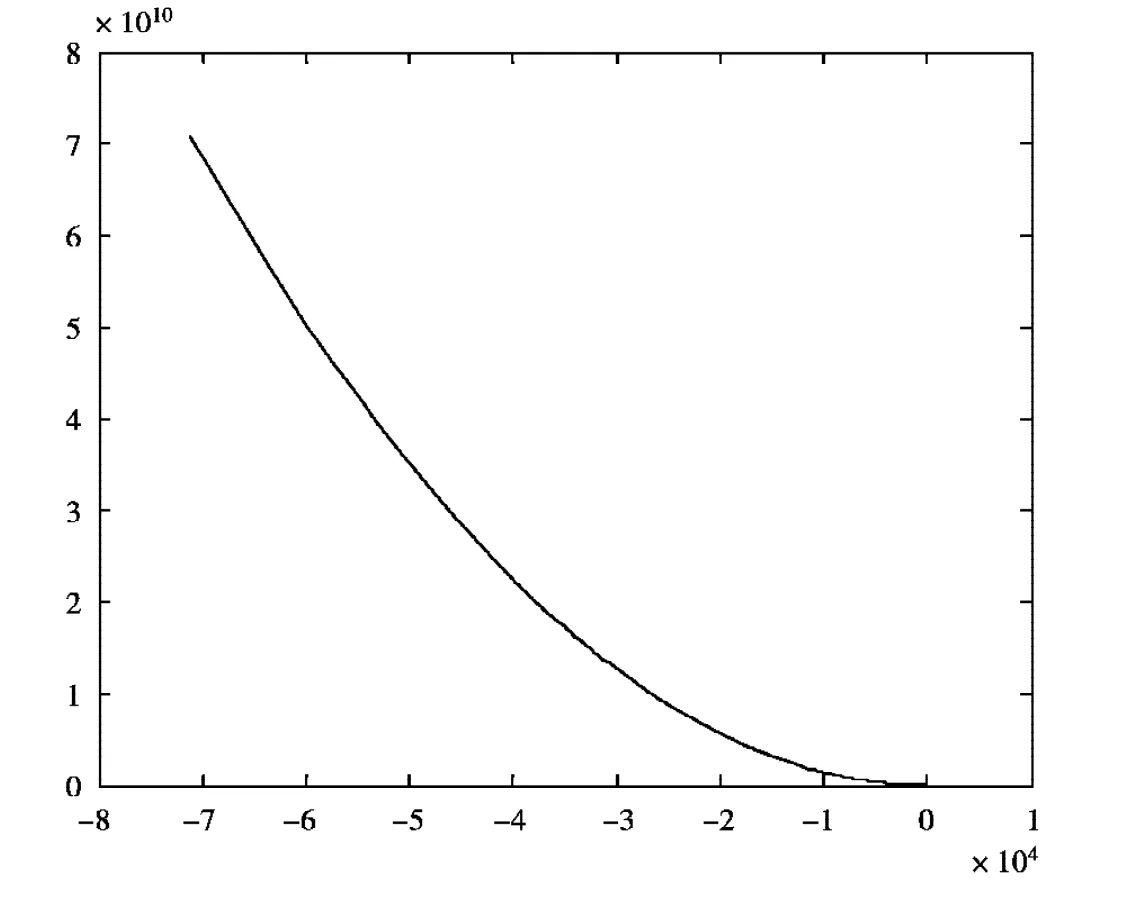
图2 平衡点不稳定时模型不存在极限环

［1］田晓红，徐瑞.一类具有HollingⅢ功能性反应的食物有限捕食-被捕食模型的极限环［J］.军械工程学院学报，2008，20(3):73-75

［2］芦雪娟，李冬梅.食饵种群具有常数收获率的具有HollingⅢ功能性反应的捕食模型的定性分析［J］.哈尔滨理工大学学报，2006，11(4):51-53

［3］何德明，窦霁红.具收获率的一类食饵捕食系统定性分析［J］.西北大学学报，2009，39(1):19-22

［4］路亚朋，张睿.一类被开发的食饵捕食系统［J］.重庆工学院学报:自然科学版，2009，23(1):157-160

［5］王继华，曾宪武.一类具有简化 HollingⅣ类功能反应的捕食 -食饵模型的定性分析［J］.数学杂志，2004，24(6):701-705

［6］吴承强 一类具有功能反应的捕食-食饵系统的极限环［J］.福州大学学报:自然科学版，2004，32(4):410-412

［7］程荣福，蔡淑云，陈军杰.一类具有功能反应的捕食 -食饵两种群模型的定性分析［J］.生物数学学报，2002，17(4):406-410

［8］陈兰荪.数学生态学模型与研究方法［M］.北京:科学出版社，1988

［9］马知恩，周义仓.常微分方程定性与稳定［M］.北京:科学出版社，2001

［10］蔡燧林，钱祥征.常微分方程定性理论引论［M］.北京:高等教育出版，1994

［11］刘启宽，张兆强，陈冲.一类具有功能反应的食饵 -捕食模型的定性分析［J］.重庆理工大学学报:自然科学版，2010，24(1):118-122