主管轴力对钢管塔K型节点极限承载力影响研究

尤 军，李正良，白 强，张 朝

(1.重庆大学 土木工程学院，重庆 400045;2.中南电力设计院，湖北 武汉 430071)

高压输变电工程是重要的生命线工程，作为主要结构的塔架，其安全性是保障大规模区域电力系统可靠性的基础。钢管塔在我国刚开始应用，国内还未对节点的构造作专门研究。目前国内外的大量研究工作主要集中在直接相贯焊接的钢管结点上，Ariyoshi等建立了该类结点试验的数据库，为各国规范公式的形成提供依据，Kim［1，2］、Wang［3］等采用有限元法对直接相贯节点应力分布进行了研究。Soh［4］、陈以一［5］、余世策［6］采用屈服线模型对钢管结点的极限承载力进行了简化理论分析，鲍侃袁［7］采用母线梁分离模型对钢管塔K型节点极限承载力进行了理论分析，其计算结果都与试验结果较为吻合。但这些研究和分析都存在一个共同的问题，基本没有考虑主管轴力的影响，或者是对轴力的影响考虑得不够充分。目前我国在设计钢管塔时较多借鉴日本的方法，在日本的《输电钢管塔制作标准》［8］中对于主管轴力对节点承载力的影响只是简单的给出了一个折减系数。但是在钢管塔的受力节点中节点的主管的轴力是非常大的，而现在的国内研究中却没有涉及到受力节点中主管的轴力对节点承载力的影响。通过一系列的有限元计算分析，以期准确的把握主管轴力对钢管塔节点的承载力的影响，为工程设计提供依据。

1 钢管塔中管-板受力特点

在高耸钢管塔中有很多种类型的管-板节点，其中K型节点具有一定的代表性，为此对K型节点进行受力分析。如图1a可知，在节点整体受力平衡的条件下要满足:

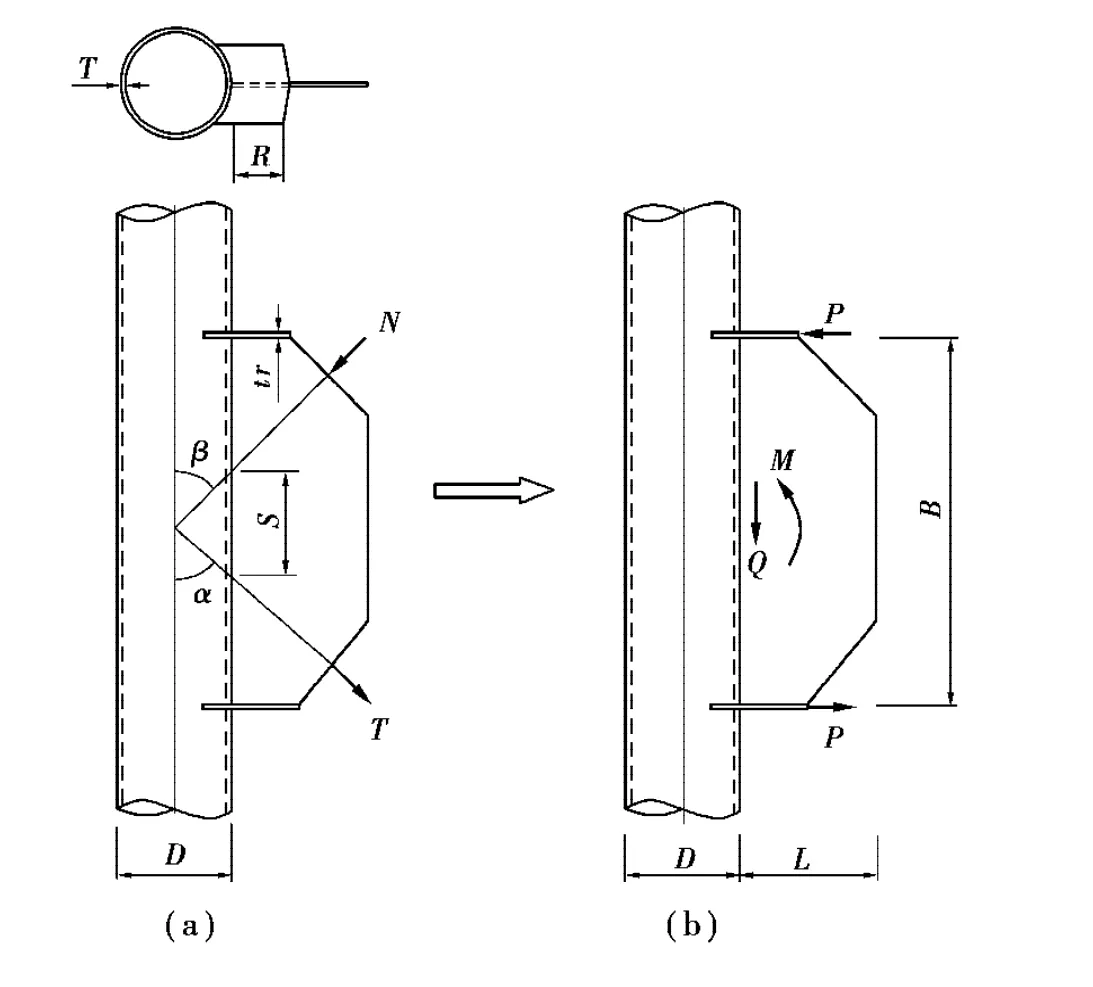
图1 K型管-板节点的结构示意图

2 数值模拟

通过建立有限元模型，并且对于不同参数下的模型的分析得到主管轴力对于节点承载力的影响情况。运用有限元程序ANSYS10.0对节点进行仿真分析，采用壳单元shell181来模拟不同参数的节点板、钢管和加强环板(图2)。

图2 有限元模型及加载方式

3 主管轴力对1/4环形加强板承载力的影响

图3 1/4加强板情况下主管轴力对极限承载力的关系曲线

3.1 不同臂长情况下主管轴力的影响情况

在日本的《输电钢管塔制作标准》中主要考虑的是节点板和主管交接处的弯矩M对于节点承载力的影响，而没有考虑到剪力Q的影响。因为这个原因，特别考察了3种不同的臂长L情况下主管轴力的影响情况。

通过有限元分析得出主管轴力在不同臂长L的情况下对1/4环形加强板情况下局部承载力的影响关系曲线(图3)，对应的极限弯矩承载力见表1。计算条件:主管规格为219×6，节点板高度B=657 mm，厚度t=16 mm，加强环板高度R=40.5 mm，厚度tr=6 mm。

从图3看出:单臂长度越短，主管轴向荷载的影响越大。臂长L为109.5 mm时节点承载力明显小于臂长为400 mm和650 mm的承载力，而臂长为400 mm和650 mm时节点的承载力则相差不大。这主要是由于剪力Q的存在影响了节点的承载力，当臂长较短为109.5 mm时剪力的影响是非常明显的，随着臂长的增加剪力的影响逐渐减弱，所以臂长为400 mm和650 mm时节点的承载力相差不大。从图3可以看出轴力在轴压比从0增加到40%时节点的承载力没有明显的下降。以后随着轴压比的增大，节点的承载力会急剧下降。在这种情况下，主管轴力对节点承载力的影响必须要引起重视。

3.2 同臂长情况下主管轴力的影响情况

从上一节可以看到主管轴力对臂长较短的情况影响是最大的，所以为了进一步弄清楚不同参数对N/Ny-KN(KN:轴力影响折减系数)关系曲线的影响，借助有限元对臂长为109.5 mm的各种参数情况下的模型进行了分析，其影响曲线如图4-图10。

从图4可以看出:当节点的最终承载力由加强环板控制时(加强环板最先发生破坏丧失承载力)主管管壁厚度不同时的承载力折减系数差值相互接近差值非常小，从上面的曲线可以看出壁厚对承载力折减系数的影响比较小。

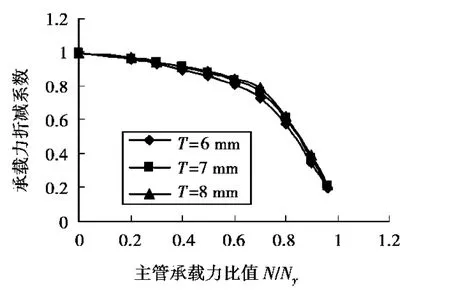
图4 不同壁厚下1/4加强板承载力折减系数与N/Ny的关系曲线(环板控制)D=219 mm，R=40.5 mm，tr=12 mm

图5 不同环板厚度下1/4加强板承载力折减系数与N/Ny的关系曲线(环板控制)D=219 mm，T=6 mm ，R=40.5 mm

从图5可以看出:不同环板厚度的承载力折减系数差值约为10%左右，环板厚度对承载力折减系数的影响比较小。(不同环板厚度的影响)说明轴压比对环板厚度较大的构件影响相对要大一些。

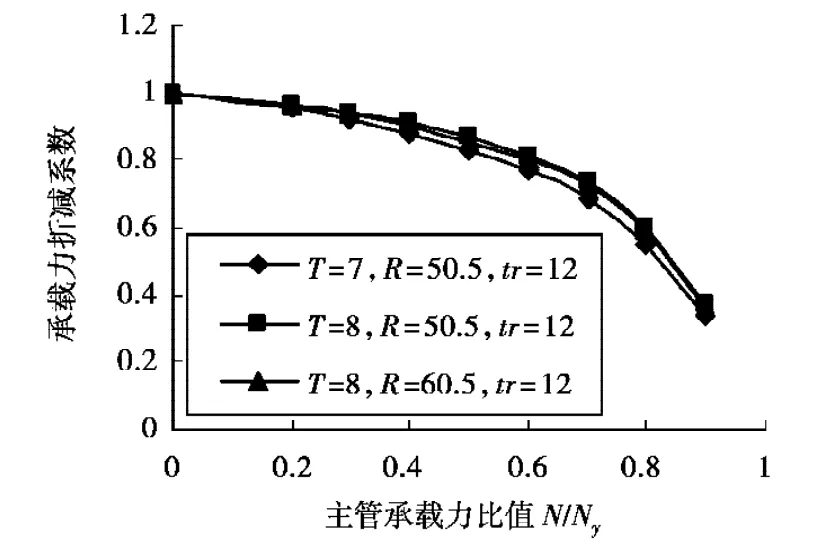
图6 不同环板宽度和钢管壁厚下承载力折减系数与N /Ny的关系曲线(环板控制)D=219 mm

图7 不同环板宽度下承载力折减系数与N/Ny的关系曲线(环板控制)D=219 mm，T=6 mm，tr=12 mm

图8 不同壁厚承载力折减系数与N/Ny的关系曲线(钢管控制)D=219 mm，R=40.5 mm，tr=12 mm

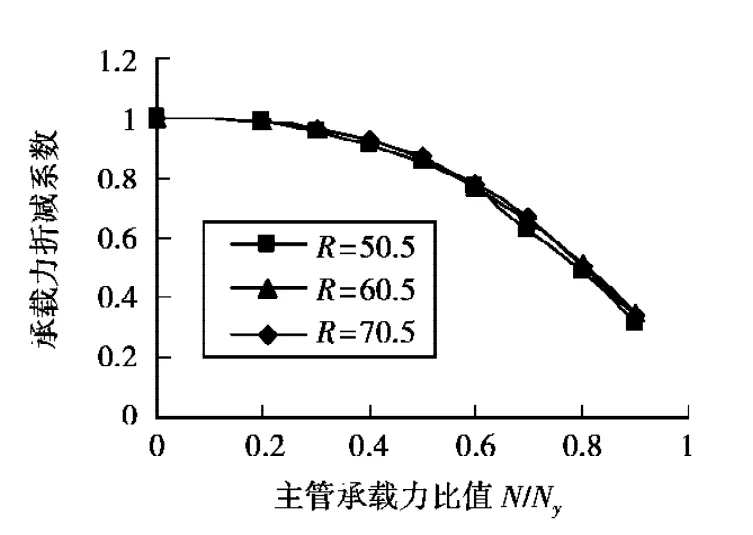
图9 不同环板宽度下承载力折减系数与N/Ny的关系曲线(钢管控制)D=219 mm，T=6 mm，tr=12 mm

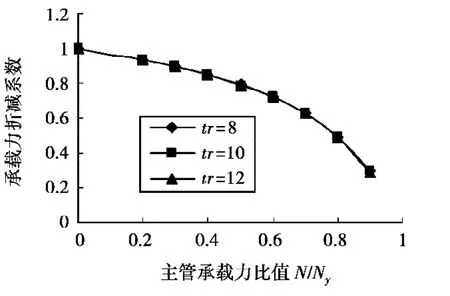
图10 不同环板厚度下承载力折减系数与N/Ny的关系曲线(钢管控制)D=219 mm，T=5 mm，R=70.5 mm

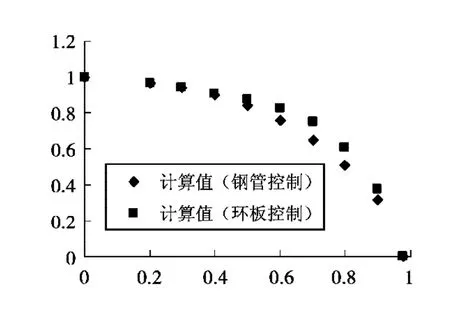
图11 1/4加强板承载力折减系数的计算值

对以上由钢管控制和环板控制在一定N/Ny值下得到的承载力折减系数取平均值，从图11可以看出:钢管控制(计算值)比环板控制(计算值)偏小，为了安全起见，并对平均值(钢管控制)进行拟合得到1/4环形加强板单侧受力折减系数曲线(图13)。

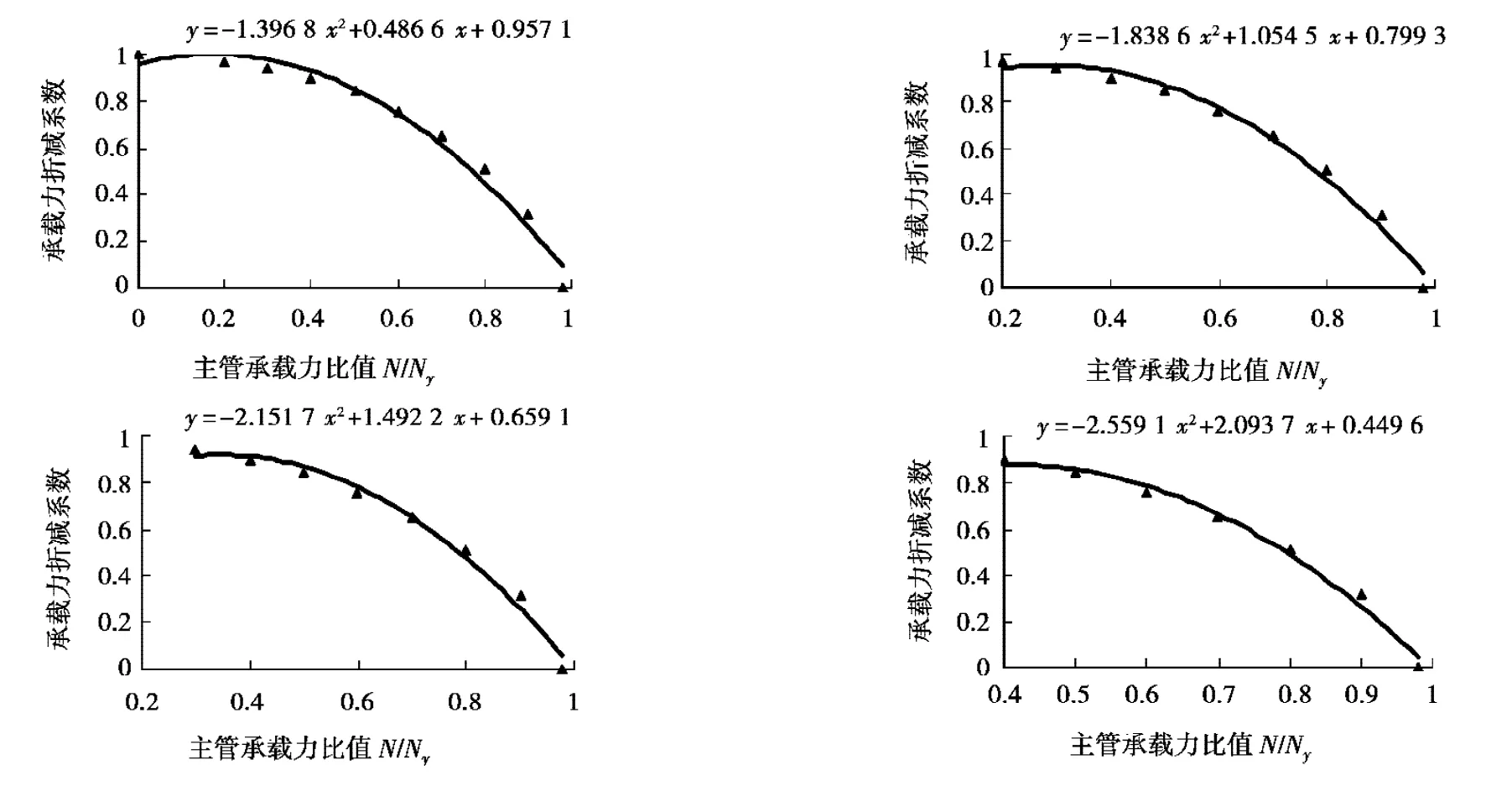
图12 不同拟合起点1/4加强板承载力折减系数与N/Ny的关系曲线

从图12可以看出:前3幅拟合曲线图都违背其实际物理意义。因为实际情况是在N/Ny=0时，承载力折减系数取得最大值为1，而不应该是在其它位置取得最大值。从0.4开始拟合的曲线在主管承载力比值为0.4～1.0之间时是逐渐递减的;根据计算数据可以看出，在0～0.4之间的数据近似看成线性递减关系，为了保证曲线的光滑性，0～0.4之间的线性函数关系通过边界条件得到，不再进行拟合。即:根据N/Ny=0时，KN=1.0和N/Ny=0.4，KN的值其值由0.4～1.0之间数据的拟合曲线确定。根据以上原则，得到1/4加强环板单侧受力折减系数曲线。

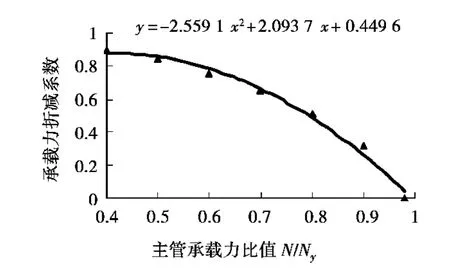
图13 1/4环形加强板单侧受力折减系数曲线

为安全起见，取主管轴力对1/4环形加强板情况下局部承载力的影响系数如下:

4 结论

对带连接板的K型钢管结点进行了有限元分析，表明对于带1/4环形加强板的K型结点的极限承载力，不仅与主管壁厚t、主管直径D、1/4环形加强板的厚度tr和高度R有关，更重要的是还和现时状态下的主管轴向力N密切相关。提出了钢管在组合外力(有轴力)作用下存在轴力影响折减系数KN，并通过数据拟合，得到了相对保守的KN的具体表达式，可以运用于实际的钢管塔设计中。

［1］KIM W.A study on connections of circular hollow section with gusset plate［J］.J Architectural Inst Korea，1997(3):101，263-271

［2］KIM W.A study on the local deformation of tubular connection in Truss［J］.Conf Korean Society of Steel Construct，1995，7(2):135-140

［3］WANG B H N，KUROBANE Y.Damage criterion and safety assessment approach to tubular joints［J］.Engineering Structure Elsevier，2000，22(5):424-434

［4］SOH C K，CHAN T K，YU S K.Limit analysis ofultimate strength of tubular X-Joints［J］.Journal of Structural Engineering ASCE，2000，126(7):790-797

［5］陈以一，沈祖炎，詹琛.直接汇交节点三重屈服线模型及试验验证［J］.土木工程学报，1999，32(6):26-31

［6］余世策，孙炳楠，叶尹.高耸钢管结点极限承载力的试验研究与理论分析［J］.工程力学，2004，21(3):155-161

［7］鲍侃袁，沈国辉，孙炳楠，等.高耸钢管塔 K型结点极限承载力的试验研究与理论分析［J］.工程力学，2008，25(12):114-122

［8］日本铁塔协会.输电线路钢管塔制作基准［S］.日本:日本铁塔协会，1985

［9］邓国红，陈超超，欧健，等.桥梁检测车臂架结构风振响应分析［J］.重庆理工大学学报:自然科学版，2010，24(5):78-82