生产性服务投入对产品竞争力的因素性贡献分析

王 文，刘 伟

（上海海事大学，上海 200135）

1 竞争力结果性衡量因素与产品竞争力构成因素

制造业的产品市场竞争力是其产业生产竞争力的体现，可以理解为产品在生产效率、满足市场需求、持续获利等方面所体现的竞争能力，表现为在一定贸易条件下所具有的开拓市场、占据市场并以此获得比竞争对手更多利润的能力[1]。

竞争力大小应该以什么指标来衡量呢？尽管各种观点存在一些差异，但总体上十分接近，如陈立敏博士（2003）认为包括利润、市场份额、生产率、投资[2]；付红波（2005）认为反映产业国际竞争力结果的实现指标包括市场占有率、盈利率、贸易竞争指数、相对出口优势指数等等，其中最重要的指标是市场占有率和盈利率[3]；金碚（1997）认为竞争力的最终体现是在国际市场上的份额[4]。可以看出，主要反映竞争力水平的是市场份额和自身盈利水平。尽管竞争力的结构可以细分为很多不同层次的指标体系，其最终目的还是要得到一个综合的结果进行评价。所以此处为简便起见，主要用市场份额MS和盈利水平PM的积来衡量竞争力E的大小。

制造业产品竞争力来源于哪些要素呢？它的结构因素包括其产品品种、质量、价格和交货期[5]，这些因素是顾客选择的出发点，因此决定了产品在市场上与其它同类产品竞争可获的利润和市场份额，也就是竞争力结果。所以产品竞争力是上述因素在一定市场环境下的函数。在现代先进制造业发展中，如电子产品和信息产品，技术含量所决定的产品功能越来越成为产品竞争力的重要因素，而品种是能够反映功能的因素。因此这里我们仍采用这四个产品竞争力因素进行研究。

2 基于生产函数结构的产品竞争力因素性函数

生产函数标准形式为：

Y为产出，A表示制度因素，K、H、L分别表示物质资本、知识技术和劳动力的投入，α、β、γ分别为物质资本、知识技术和劳动力的产出弹性。

竞争力与竞争力因素虽然不是物质生产关系，竞争力属于抽象产出，但它们的逻辑关系是相似的。生产函数反映出产量或经济效益是各投入要素综合作用的结果，而竞争力是由各竞争力要素综合作用而成，竞争力要素集合{品种V、质量Q、价格P、交货期T}对竞争力E的产生基本完备，这些要素是构成竞争力的充分必要条件，能够比较完整地构成竞争力，而且缺少任何一个都不能构成竞争力。

此外，很多针对具体问题的研究都在此函数形式基础上加入其他要素和指数来研究经济发展的相关问题，如国内外投资与中国经济增长[6～8]、出口贸易与经济增长[9]、金融要素与经济增长[10]、国际贸易与中国城市化[11]、技术创新能力与产品竞争力[12]、技术进步与经济增长[13]、交通投资与经济增长[14]、产业内贸易与经济增长[15]等。

由此，构建产品竞争力与其要素的函数关系为：

E为产品的市场竞争力，A同样表示制度因素，V、Q、P、T分别为产品品种、质量、价格、交货期，α、β、γ、θ为各要素的竞争力弹性指数，反映各要素的贡献程度。如前所述，用竞争力结果性因素市场份额MS与利润率PM的乘积来衡量产品竞争力的大小，则有：

3 生产性服务投入对产品竞争力的因素性贡献分析

根据上述分析，如果已知指数参数，就可以用贡献率的定义得到各因素对竞争力的作用。变量x对y的贡献率R的算法为

即单位产出需要的相应的要素的量。竞争力曲线上两点间的因素的贡献率分别为，而曲线上某点处因素的贡献率即为该点处竞争力因素对竞争力的导数。因此竞争力曲线上某点处各因素对竞争力的贡献率如表1。

表1 竞争力因素的点贡献率

一件产品在市场上被最终消费，除了生产过程中物质资料的投入，还有很多生产性服务的投入，如生产管理、物流服务、顾客服务等。我们经常需要衡量这些服务对最终产品竞争力的效率和作用，以对生产性服务进行评价、比较和决策。它们对产品竞争力的贡献固然可以以其价值差按（5）直接计算，但这只能反映出增加每单位竞争力上耗费的价值，无法看出这些投入是在哪些方面、通过什么途径对产品竞争力发挥作用的，从而无法知道如何提高其效率。在不考虑信息约束和产品可获性的条件下，所有投入都是通过在竞争力结构性因素上发挥作用而影响产品竞争力结果的，此时产品竞争力只与产品本身性质有关，与数量无关。因此通过考察生产性服务投入对竞争力结构性因素的作用，又知道竞争力结构性因素对竞争力的贡献，就可得到该种服务投入对产品竞争力的贡献，同时也能看出它在不同方面发挥作用的能力大小。另一方面，当市场对竞争力结构性因素的偏好发生变化时（竞争力函数的指数参数发生变化），我们可以知道哪些生产性服务对保持产品竞争力起重要作用，能以同样的投入价值获得更多的竞争力。

此处定义某因素的变化引起的竞争力增量为该因素对竞争力的贡献，就是它带来了多少竞争力。设某生产性服务业 S 分别使各竞争力要素由 V0、Q0、P0、T0变为 V1、Q1、P1、T1，则它通过这些因素产生的对产品竞争力的贡献为：

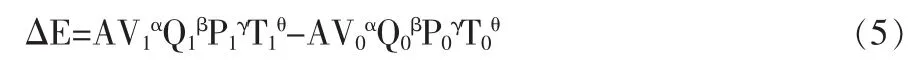
表2 某项生产性服务投入对产品竞争力的因素性点贡献

如果竞争力结构性因素变化量非常小，可以用竞争力曲线上该因素点处的导数与因素变化量的积来求其贡献。例如V对E在曲线上某点处的贡献EV为

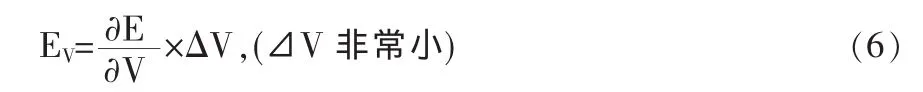
这样，各因素对产品竞争力的点贡献为其贡献率的倒数与因素变化量的乘积，S在各因素上对产品竞争力的点贡献为其引起的因素变化量与因素点贡献的乘积，见表2。

这种基于生产函数结构和结构性因素点贡献的分析方法尤其适合于研究生产性服务业对产品竞争力的贡献问题。因为它们是生产的辅助部分，对生产起促进和服务的作用，对产品竞争力的影响不像实物产品和材料那样显性和直接，一般情况下它们引起的各竞争力因素的变化量不大（物流对时间因素的影响除外），加上短期内生产条件、技术水平、贸易条件、政策等变化不大，可以认为竞争力函数的参数不变，这样就可以按表2计算其贡献。如果生产性服务引起竞争力结构性因素较大的变化，可用（5）式计算其对产品竞争力的贡献。

4 指数参数的R程序估计

为便于进行参数估计，通常将（2）式两边取自然对数，

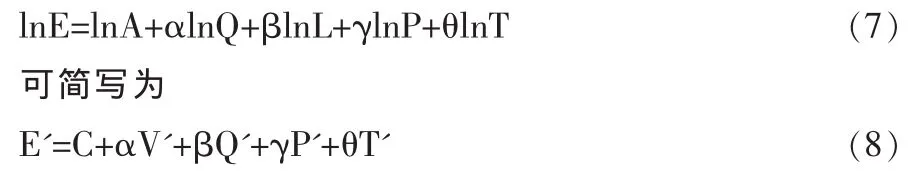
可以用相应的统计分析工具按式（7）、（8）的思路进行参数估计和检验，再由可接受的参数来估计和预测样本以外其它情况的竞争力及某项投入的贡献。

此处举例说明使用R软件计算函数的参数。设某产品竞争力因素值如下：

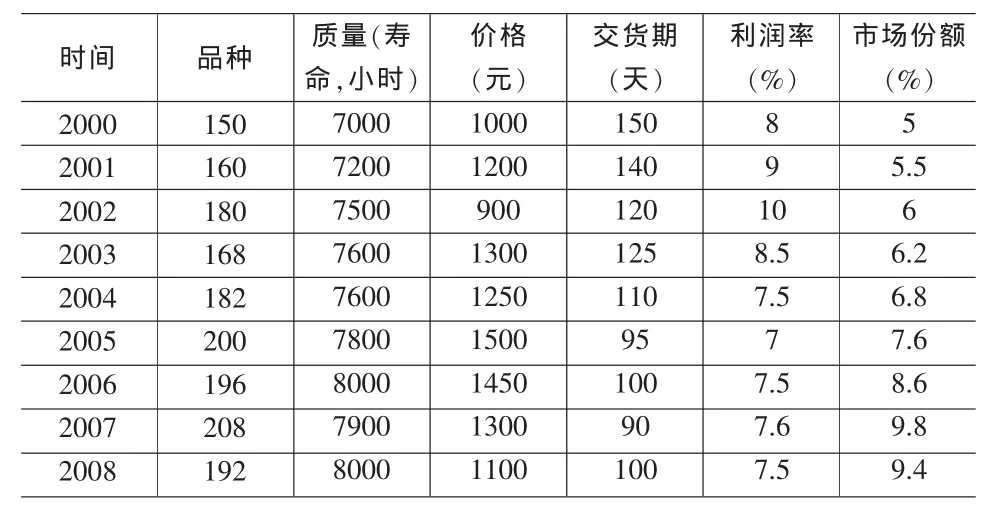
表3 某生产行业产品竞争力因素值

参数估计的部分R程序、结果及分析如下：

4.1 构建数据框，计算竞争力数值

得 到 9 个样本相应的竞 争力值：40.00、49.50、60.00、52.70、51.00、53.20、64.50、74.48、70.50。

4.2 对数线性模型分析

结果如表4。

首先得到9个样本值与估计值的残差，Coefficients数据框estimate列为模型参数的估计值，常数项及α、β、γ、θ估计值分别为-45.4765、2.4202、3.7066、-0.3412、1.3164，Std.Error列为参数标准差，最后两列分为为参数的t值和P值，都不是十分显著。模型残差标准差为0.09981，自由度为4，相关系数的平方为0.8681，说明模型相关性较强，F统计量为6.582，自由度（4，4），模型P值显著，说明回归方程通过检验。

4个对数变量的方差自由度均为1，只有残差的方差自由度为4，因此4个对数变量的方差平方和与均方相等。时间因素对数的偏差量较小，而种类因素对数的偏差量明显偏大。种类因素的对数变量P值显示一个*说明显著，其它变量都不显著（表5）。

4.3 预测非样本点的函数值

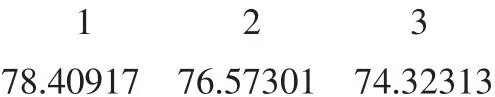
由样本得到的函数模型预测3个非样本点的线性函数值，同时预测相应的原始因变量——竞争力变量的值。

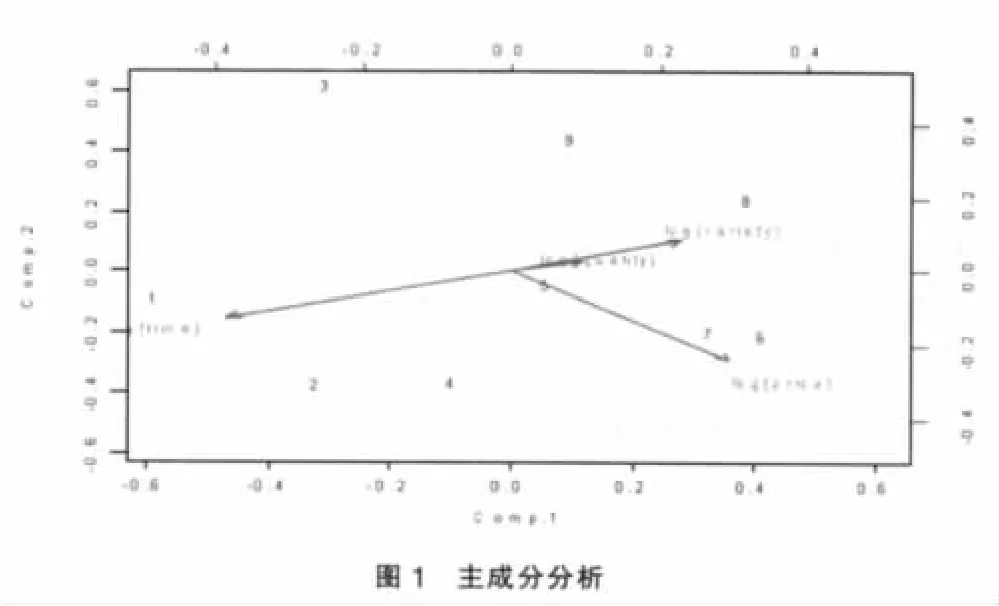
4.4 函数模型的主成分分析

图1结果显示，第一、第二主成分的标准差较大，第一主成分的方差贡献率最大，第一、二主成分的方差累积贡献率已达到99%，由各中间变量的载荷可以得到主成分的变量表达式，由于前两个主成分的累积贡献率已相当高，后面两个主成分可以舍去，对函数达到降维的目的，即

如果第一主成分的值较大，说明总体上产品种类较多、质量较好、价格较高、交货期较短；如果其值较小，说明总体上产品种类较少、质量一般、价格不高、交货期较长。如果第二主成分值较大，则可能是产品种类较多、质量较好、价格较低、交货期较短；如果其值较小，可能是产品种类较少、质量一般、价格较高、交货期较长。第一第二主成分的直方碎石图显示第一主成分的方差明显高于第二主成分方差。品种对数变量和质量对数变量的坐标在主成分下的方向很接近，与时间对数变量的方向几乎相反，第一第二主成分的样本散点图显示样本 6、7、8的品种、质量、价格都较高而交货期较短，属于优势型，样本1、2、3属于劣势型，样本5属于中间型。

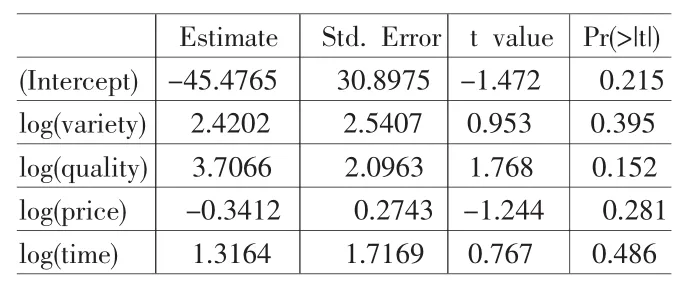
表4 相关系数

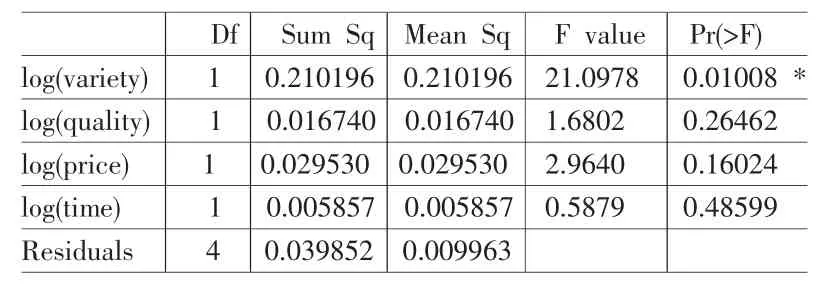
表5 对数变量方差值

5 结论

制造业的产品竞争力由其在市场上的种类、质量、价格、交货期等因素构成，竞争力大小可由其在市场上获得的占有率和利润水平衡量。可用生产函数的形式构建产品竞争力函数，为竞争力结构性因素幂的乘积。生产性服务投入在某竞争力结构性因素上产生的对产品竞争力的贡献等于它引起的因素变化量与该因素贡献率或点贡献率倒数的乘积。这种方法为非物质性的生产性投入对产品竞争力的贡献找到了一种桥梁，使之具体、直观。

[1]包学松，王雪芳，童章成.竞争力经济学概论[M].北京:国家行政学院出版社，2006.

[2]陈立敏，谭力文.产业国际竞争力的评价方法研究[J].经济管理新管理，2003，(24).

[3]付红波.我国茶叶产业国际竞争力研究[D].雅安：四川农业大学，2005.

[4]金碚.2006中国企业竞争力报告[M].北京:社会科学文献出版社，2006.

[5]郭凤梅.制造业生产物流理论及应用研究[D].武汉：武汉科技大学，2003.

[6]王兰.FDI对中国经济增长的贡献度分析[J].企业经济，2004，(9).

[7]项喜，沈毅俊，陈彦吕.外商直接投资对浙江经济增长的贡献度测算[J].浙江统计，2005,(2).

[8]欧阳志刚.外商直接投资及其对经济增长的贡献[J].财经科学，2004，(6).

[9]Chen Rui,Wang Jian.Research on Regional Differences between China's Economic Growth and Export Trade Based on the Analysis of a Random Effects Model[J].Data Science Journal,2007，6.

[10]董积生.对经济增长中金融要素贡献度的实证分析[J].科技与经济，2005,18(1).

[11]王家庭.国际贸易对中国城市化贡献的测度研究[J].上海经济研究，2005,(8).

[12]Tanel Gary.Sourcing Manufacturing Innovation[J].SMT Surface Mount Technology Magazine,2006,20(2).

[13]张炎涛，李伟.技术进步对湖北省经济增长的贡献度[J].统计与决策，2007，(3).

[14]高峰，范炳全.交通投资对经济增长贡献理论的评价[J].淄博学院学报自然科学与工程版，2002，4(1).

[15]黄景贵，李丽.中国与主要贸易伙伴国间的产业内贸易对经济增长的贡献分析[J].中国经济评论，2006，6(5).