企业内部利益相关者结构理论的博弈分析

金 静

（安徽财经大学 会计学院，安徽 蚌埠 233030）

0 引言

近年来的研究表明公平互利偏好对社会经济活动具有广泛影响。譬如，企业政策的公平性将影响员工的努力程度，甚至是员工的偷窃行为（Bewley,1999）。公平互利规范的存在可能使直接消减工资变得无效率，因为人们采用间接的方式降低了工资成本（Agell和Lundborg，1995）。实验经济学研究发现互利行为对社会规范的维持 （Fehr和Giichter，2000a），不完全契约的执行 （Fehr、Giichter和 Kirchsteiger，1997；Fehr和 Giichter，2000a），工资粘性（Fehr and Falk，1999）以及工作激励（Fehr和Giichter，2000a）都具有重要影响。

经济学家曾提出一些模型解释个人的互利行为，如Rabin（1993）通过心理博弈方法构建了一个纯意图模型。该模型忽略了参与者对收益分配的偏好，而且局限于两个标准式博弈，没有对非均衡路径中的信念形成做出设定，当应用于序贯博弈就会产生不合理的均衡，Fehr和Schmidt（1995）与Bolton和Ockenfels（2000）则从收益差距厌恶角度来解释参与者的互利行为，但却忽略了互利行为中最重要的意图因素。Falk和Fischbacher（2000）在心理博弈框架下构建了一个综合收益分配与意图因素的互利模型，克服了纯意图模型与收益差距厌恶等模型的缺陷。但仍然存在以下缺陷：①不能确保互利均衡的存在；②对意图的考虑具有局限性。

本文试图克服F-F模型的缺陷，构建一个较为完善的公平互利模型来探索所有者，债权人和经营者三者之间公平互利行为的结果，为公司治理结构提供新的研究视角。

1 模型设定及相关证明

我们根据F-F模型的新公平概念构建了所有者，债权人和经营者的三者意图函数，使得该函数的参考者的战略与信念空间上具有连续性，从而保证均衡的一般存在性，克服了F-F模型的缺陷。

考虑一个完全信息下的互利博弈，参与者i=1，2，（指经营者与投资者）它们皆序贯行动。参与者i的行动集为Ai，博弈终点集为E，设博弈的支付函数为：π1i:E→R。参与者i的行为战略为的一阶信念为的二阶信念为经营者的人力资本增值率

在标准博弈模型中，参与者是根据自己的一阶信念来最大化自己的效用，而在互利博弈中，参与者将自己的一阶信念和二阶信念来判断对方善意水平以及风险意图水平，所以善意函数的设定是互利模型的关键。

1.1 善意函数φ

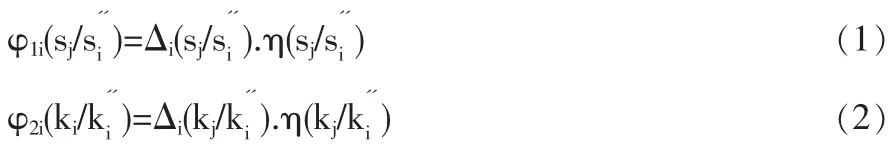
1.1.1 公平函数Δ

不同于F-F模型，我们将参与者i应该得到公平收益定义为：给定参与者i的战略下可以得到的期望收益，最大可行的帕累托改进收益与最小可能收益的平均。

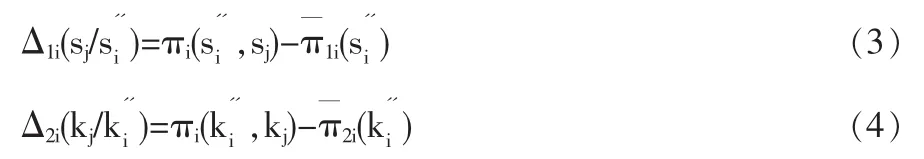
1.1.2 意图函数的判断

这里意图函数Ω1i实质是Ω2i的条件意图函数，因为ki=hi/si，所以π2i的产出变量以π1i为前提条件。虽然它们都是参与者i的战略空间与信念空间下具有连续性。这里Ω1i，Ω2i是参照系下的意图函数，根据F-F模型的设定，在参照系意图判断函数η为：

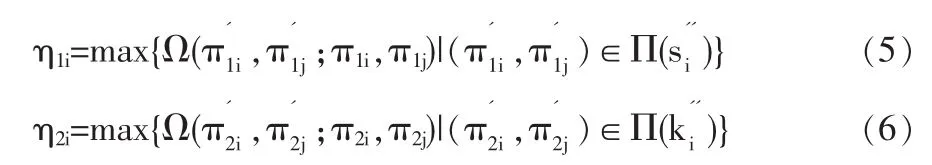
1.2 互利函数σ

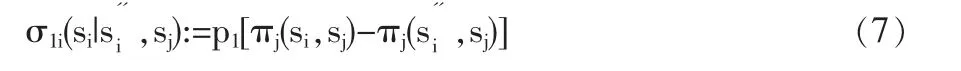
（7）式对于所有者对债权人来说，其两者的差为i对j的互利水平。

1.3 互利效用函数

互利博弈参与者的效用由两部分构成：私人收益与互利性心理收益。其中，φ和σ如（1）～（8）式的定义。在信念下，经营者人力资本价值增值率，投资者对其产生信念i选择战略ki时互利效用函数为：

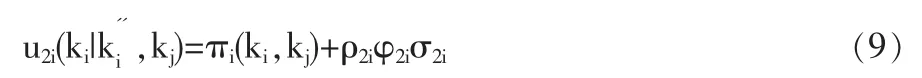
参数ρ1i，ρ2i为参与者i的互利程度。当善意函数φi为负时，选择小于0的互利水平σ将提高参与者的效用，说明此时参与者i就倾向于惩罚j，反之将选择大于0的互利水平σ来回报j，即使这种惩罚或回报会降低自己的收益。当ρni→0(n=1,2)时互利模型就等价于传统的自利博弈模型。根据非完全理性博弈人性假设，惩罚性互利与回报性互利往往不对称，那么ρni应该变化。

1.4 互利均衡定义及其存在性

我们将心理博弈引入其中，把两人博弈扩展到四人博弈，其中参与者效用函数由投资者与经营者，所有者与债权人的式子所定义，其他与传统的两人扩展博弈相同，参与者的效用不仅取决于双方战略选择，而且依赖于参与者的信念，但信念与战略不兼容。当经营者与投资者在给定信念下选择最优战略使经营者对投资者及自身贡献最大情况下，投资者中所有者与经营者之间按最优资本结构配置权力分配资源，即公司治理结构的最根本前提，这个前提也反作用经营者与投资者之间信念确定。与纳什均衡比较，心理博弈中的纳什均衡要求信念必须与战略相匹配，即信念一致性。

下面给出互利均衡的正式定义。

定义：四人扩展博弈Γp，记其子博弈集合为：

{Gn，n=1，2，…，m；gn，n=1，2，…，m}一组战略(s1，s2)是互利均衡，另一组根据战略(s1，s2)互利均衡形成该组战略(k1，k2)是互利均衡，如果满足：

（1）子博弈精炼均衡条件：

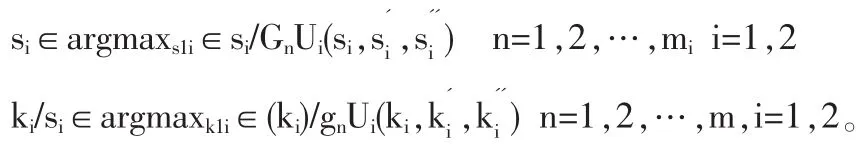
（2）信念一致性条件：

信念传递条件：

当ρ1=ρ2=0时，互利均衡就是原博弈的纳什均衡。

定理1：互利均衡存在性

证明：我们先讨论经营者与投资者之间心理博弈Γp，参与者具有完全信息，而且参与者行动可观察。下面我们采用Ferdunberg和Tirole（1991）中的代理人战略形式：在每一个结点上似乎有一个代理人进行行动。代理人战略式中的最优战略组合对应于原博弈的一个子博弈精炼均衡。

（1）记号与基本约定及证明（经营者与投资者）

sn={(pa)a∈An|pa∈[0，1]，Σapa=1}是在这个结点上的混合战略集。 记 s=πn∈Nsn是参与者战略组合，记 s-n=πm≠nsm是所有其他结点上的战略组合集，战略组合 s=(sn，s-n)，其中 sn∈Sn，s-n∈S-n，s'和s''分别为参与者的一阶信念和二阶信念。记Vn.(sn，s-n)，s'，s''是在结点n上的条件期望效用，即给定战略与信念，当博弈进行到结点n时参与者的期望效用。对于所有者与债权人来说，信念传递，记他们互利效用函数且为连续函数，由于信念具有传递性，且结点相同，各种战略集合均是在前一种战略组合基础形成新战略组合。前一种行为战略组合形成条件期望效用函数却是后一种的条件期望效用函数前提。由于它们具有一一映射关系，我们只讨论前者互利均衡存在，那么后者同理可证明。

约定最优反应函数B且

因为Sn是凸紧集，而S∈SN，所以S是一个紧集。u1i(es'')是参与战略的连续函数，故在结点n上的V在Sn上连续，所以 B(s)为非空。 同时 B(s)为凸集（如果 B(s)非凸，那么∀s'，s2∈B(s)和 λ∈(0，1)使得 λs'+(1-λ)s2∉B(s)。 但对于每个节点 n 都有：

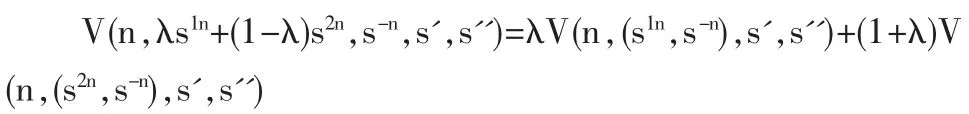
这样与假定相矛盾，故B(s)是凸集。

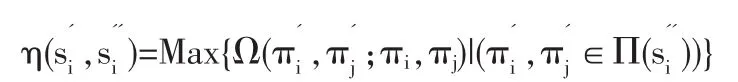
根据最大值定理，我们得到最优反应函数B是上半连续的，应用Karutani不动点定理，得到存在战略组合s*∈B(s*)⊂S。这一战略与一阶信念和二阶信念就组成一个互利均衡，其组合显然满足信念一致性条件，同理得到投资者之间互利均衡，故心理博弈中互利均衡存在性得以证明。

（2）记号与基本约定的所有者与债权人双赢与双损均衡证明

我们现在讨论投资者中所有者与债权人的序贯行动，假设投资者与经营者互利合作产生总净产出为W，首先由提议者提议一个分配比例，设分给回应者的份额为x，然后由回应者决定接受（A）或拒绝（B）这个提议。如果接受，两人得到提议者所提出的分配份额，即，π1(x,A)=W-x，π2(x,A)=x；如果拒绝，双方的收益都为0，即π1(x,R)=π2(x,R)=0，在不影响模型性质的条件下，为了简化分析，我们设定W=1。

记提议者的战略为 x∈[0，w]，回应者战略为 P∈[0，1]，根据非完全理性博弈人性假设中，存在“以德报德，以怨报怨”现象。因此我们作如下定义：

定义1：双赢性均衡：如果(x，p)是一个均衡，而且在该均衡下至少有一个参与者认为对方的行为是善意，那么就称(x，p)为双赢性均衡。

定义2：双损性均衡：如果(x，p)是一个均衡，而且在该均衡下每一个参与者都认为对方的行为不具有善意或含有恶意，那么就称(x，p)为双损性均衡。

根据定义1、2，在完全信息中，具有如下均衡：

①如果双赢参数ρ1与ρ2都大于零，那么博弈存在以下双赢性均衡：

③如果ρ1与ρ2其中一个为0，那么均衡就取相应的极限值。

④如果ρ1与ρ2都为零，那么均衡就为：

证明：提议者的战略空间为s1={x:x∈[0，1]}，回应者的战略空间为 s2={p:p∈[0，1]}。 给定战略选择(x，p)与二阶信念(x''，p'')双方的期望得到的公平收益水平分别(p'')=1/2p''。因为假定这是一个完全信息博弈，所以双方的双赢倾向ρ1和ρ2为共同知识。

（3）回应者的最优反应

给定回应者的二阶信念p''，我们得到回应者的公平函数Δ2(x|p'')=(x-1/2)p''。当x≥1/2时，回应者认为对方具有善意，而且提议者没有选择损人利己的提议，根据意图因子的设定有η2=1；当x＜1/2时，回应者认为对方的分配不公平，但此时如果对方要公平对待自己将损害其自身的利益，所以意图的强弱由双方的得益损失比来决定，根据我们的设定η2=min同时根据定义，互利因子函数(p-p'')。当x≥1/2时，回应者的最优选择是p=1。当x＜1/2时，

（4）提议者的最优战略

给定回应者的最优反应p(x)和提议者的二阶信念x''，得到参与者的公平函数：Δ1(p(x)|x'')=(1-x'')(p-1/2)。当p＞1/2时，公平函数大于0，回应者对提议者有一定善意，但对回应者而言是一项利己利人的选择，意图强度取决于相对受益水平，所以根据模型的设定得到

当p＜1/2时，公平函数小于0，回应者的选择对提议者显然没有善意，而且相对于任何p'＞p是一项损人损己的选择，所以有η1=1。

通过数值计算可以得到，对于任意的ρ2＞0都存在一个临界互利水平存在一个稳定的解。

同理我们可以证明经营者和投资者在完全市场上的双赢均衡或双损均衡。

3 结论

本文运用博弈论理论探索了企业内部利益相关者结构理论中以人为本的和谐思想，阐述了经营者与投资者在不完全理性的博弈人性的假设中的和谐博弈均衡，以其为条件探索了所有者和债权人的和谐博弈均衡，同时文中证明它们的存在，揭示了企业内部利益相关者结构的优化是序列博弈的过程，为公司治理结构科学发展提供新的视角，为我国资本市场的改革指明了发展方向，它是以人为本的和谐社会的社会主义市场理论的一部分。

[1]Bolton G.E.,and A.Ockenfels,A Theory of Equity,Reciprocity and Competition,American Economic Review,2000,90,166-93.

[2]Charness,Gary and Matthew Rabin,Understanding Social Preferences with Simple Tests，Quarterly Journal of Economics,2002,117,817-869.

[3]Falk,A.and U.Fischbacher,A Theory of Reciprocity,Institute for Empirical Research in Economics,Working Paper No.6,U-niversity of Zurich,2000.

[4]Fehr,Ernst,Georg Kirchsteiger,and Arno Riedl,Does Fairness Prevent Market Clearing?An Experimental Investigation,Quarterly Journal of Economics,1993,108,437-59.

[5]Fehr,Ernst,and K.M Schmidt A Theory of Fairness,Competition,and Cooperation,Quarterly Journal of Economics,1999,114,817-68.

[6]Rabin,M.,Incorporating Fairness into Game Theory and Economics,American Economic Review,1993,83,1281-1302.