贝叶斯决策的变精度概率粗糙集模型

李丽红，王金朋

（河北理工大学 理学院，河北 唐山063009）

0 引言

粗糙集理论[1]自提出以来在诸多领域得到了迅速发展和成功应用[2]，但在实际应用中发现[3]Pawlak粗糙集模型的一个局限性是它所处理的分类必须是完全正确或是肯定的。变精度粗糙集模型[1]的提出扩充了Pawlak粗糙集模型，其中的变精度思想是在基本粗糙集模型的基础上引入了参数β（0≤β＜0.5），即允许一定程度的错误分辨率存在，参数阈值范围可以根据变精度粗糙集近似约简标准确定[4]。概率型粗糙集模型[1]利用了信息系统中的不完全性和可能存在的统计信息，为研究自然界大量的随机现象，处理由随机产生的知识库的数据[1]，提供了一个符合实际规律的反映，由于概率粗糙集中的两个参数α和β并无严格的条件约束，可能因此造成的对论域U中的一些概念刻画失真，变精度概率粗糙集模型[5]使这一问题得到改善。贝叶斯决策理论和方法作为统计模式识别的基本方法[6]，是在分类错误发生的概率最小的前提下进行分类。讨论贝叶斯决策过程，建立贝叶斯的概率粗糙集模型[7]实现了利用概率型粗糙集分析具有最小风险的贝叶斯决策问题，但在实际的应用中寻找合适的损失函数是极不容易的[6]，因此通过损失函数得到合理的参数，也是十分困难的。本文将分析贝叶斯决策过程，在提出合理的损失函数基础上，讨论贝叶斯决策问题和变精度概率粗糙集模型的联系，建立贝叶斯决策的变精度概率粗糙集模型。

1 变精度概率粗糙集模型

定义1[1]设U是有限论域，集函数P：2U-[0,1]称为概率测度，若

（1）P（U）=1

（2）当 A∩B=Φ 有 P（A∪B）=P(A)p(B)

定义2[2]令

其中|X|表示集合X的基数，称c(X，Y)为集合X关于集合Y的相对错误分辨率。

定义3[1]设U是有限对象构成的论域，R是U上的等价关系，其构成的等价类为

U/R={X1，X2，…，Xn}

记x所在的等价类[x]，令P为定义在U的子集构成的σ代数上的概率测度，三元组AP=(U，R，P)称为概率近似空间。U中的每个子集称为概念,代表了一个随机事件。

定义4[5]设U是有限论域，限定0.5＜α≤1，对任意X⊆U,定义X关于概率近似空间AP=(U，R，P)依参数α的下近似

其中：[x]是与对象x具有相同描述的对象的全体，亦称为x的描述。

x关于AP依参数α的概率(I)型正域，边界和负域分别为：

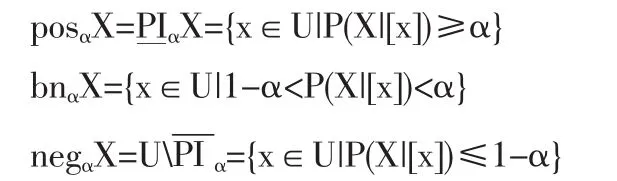
变精度概率粗糙集模型，通过限定参数a(0.5＜α≤1)的取值范围，α可认为是分类正确率，变两个参数α、β为一个参数，充分地利用了近似空间中尽可能多的有用信息，比较客观、准确地反映了被认识对象的本质属性，以及数据之间的相关性，从而降低了决策失误的风险。若令：

且取β=1-α，则模型就变为普通意义下的变精度粗糙集模型。

2 最小风险的贝叶斯决策

贝叶斯决策理论和方法是统计模式识别的基本方法。基本原理是：有相似性的样本在模式空间中互相接近，并形成“集团”，即“物以类聚”。在最小风险的贝叶斯决策过程中，引入风险的概念，利用事件发生的先验概率，以求采取某种决策的风险最小。

设 Ω={X1，X2，…，Xs}是具有有限个特征状态的集合，每个集合 Xi是 U 的子集，通常称为概念，A={r1，r2，…，rm}是由 m个可能决策行为构成的集合，P(Xj|[x])表示一个对象在描述[x]下处于状态Xi的概率；一般假定P(Xj|[x])是已知的，令λ(ri|Xj)表示状态为Xj时采用决策ri的风险损失，一般是根据所研究的具体问题，分析错误决策造成损失的严重程度，与相关的专家共同商讨确定。

假定一个对象的描述为[x]，对于这个对象实施决策ri，则对象在给定描述[x]下采用决策ri的期望损失（条件风险）可由全概率公式得：

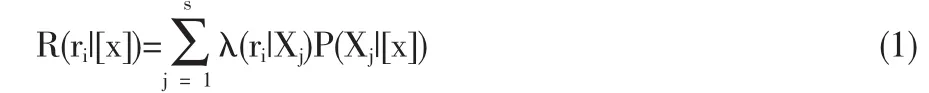
对于每一个[x]，都对应着一个随机的观测值，对于不同的描述[x]，采取决策ri时，其条件风险的大小是不同的，因此究竟采取那一种决策，随[x]而定，若将决策rj可以看为对象x函数，记为r(x)，则总体风险为：

在考虑错判带来的损失时，我们希望损失最小，如果在采取每一个决策或行动时，都使其条件风险最小，即保证每个观测值下的条件风险最小，则总体期望风险最小。最小风险贝叶斯决策可按下列步骤进行[6]：

（1）∀x∈U，利用 P(Xi|[x])及损失函数值 λ(ri|Xj)，按式(1)计算出采取 ri(i=1，2，…，m)，的条件风险 R(ri|[x])。

（2）对步骤（1）中得到的 m 个条件风险值 R(ri|[x])(i=1，2，…，m)进行比较，找出使条件风险最小的决策rk，即

则rk就是最小风险贝叶斯决策。

3 贝叶斯决策的变精度概率粗糙集模型

引理1[7]设U为有限对象构成的论域，X为U的子集，则特征状态集合Ω={X，-X}。

引理2[7]概念X将论域U分为三部分：pos(X)，neg(X)，bn(X)。

定理 对论域U上的概念X，若X具有最小风险的贝叶斯决策问题，则必存在一个等价的变精度概率粗糙集模型。

证明：（1）由引理 1知，论域U被分为两部分：pos(X)和neg(X)。

（2）由引理 2知，概念 X将论域U分为三部分：pos(X)，neg(X)，bn(X)。对于论域中的每个对象x，其描述[x]都面临三中可能的决策（肯定决策（Y），否定决策（N），待定决策（D））

（Y）决策 r1:x∈pos(X)，即 r1:[x]→pos(X)

（N）决策 r2:x∈neg(X)，即 r2:[x]→neg(X)

（D）决策 r3:x∈bn(X)，即 r3:[x]→bn(X)

这时决策行为集合 A={r1，r2，r3}，令 λ(ri|X)为特征集合 X采取决策ri的风险损失；λ(ri|X-X)为特征集合-X采取决策ri的风险，P(X|[x])为对象在描述[x]下处于状态集合X的概率，P(-X|[x])为对象在描述[x]下处于状态集合-X的概率，所以，x在描述[x]下采取决策ri的条件风险为：

其中：λi1=λ(ri|X)；λi2=λ(ri|-X)；i=1，…，m。

由贝叶斯决策过程可得最小风险决策规则：[1]

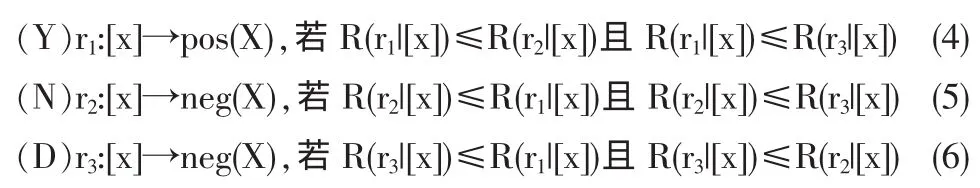
由全概率公式知：P(X|[x])+P(-X|[x])=1，可得P(-X|[x])=1-P(X|[x])，将其代入到决策规则中，并把式（3）也带入到决策规则当中，例如我们带入式（4）可以得到：

R(r1|[x])=λ11P(X|[x])+λ12P(-X|[x])

R(r2|[x])=λ21P(X|[x])+λ22P(-X|[x])

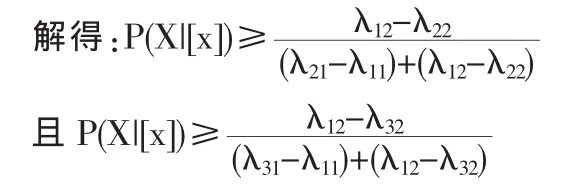
由上面的推导可知：对于任意的x属于U，最终选择哪个决策行为，只与对象x的描述[x]处于特征集合X的概率有关，即与P(X|[x])的大小有关系。

在实际情况中，须选择合适的风险损失λij(i=1，2，3；j=1，2)，才能得到合理的决策规则，选择不同的决策自然得到的风险损失是不一样的，对特征集合X，若选择肯定的决策r1，则认为风险不大于选择r3，选择r3的风险小于于选择r2，即有：λ11≤λ31＜λ21，对于特征集合-X 有 λ12＞λ32≥λ22。 为减小决策失误的风险，对于风险损失函数我们加强约束条件：

计算可得最小风险决策规则表达为：

(Y)r1:[x]→pos(X)，若 p(X|[x])≥α，p(X|[x])≥γ

(N)r2:[x]→neg(X)，若 p(X|[x])≤γ，p(X|[x])≤β

(D)r3:[x]→bn(X)，若 β≤p(X|[x])≤α

其中：

由风险损失的约束条件知：α∈[0.5，1]，又由待定决策r3知：参数满足β≤α，以下分两种情况讨论。

（1）若 β＜α，显然有 β＜γ＜α 且 β=1-α，这时可能的决策变为：

（Y）r1:[x]→pos(X)，若 p(X|[x])≥α

（N）r2:[x]→neg(X)，若 p(X|[x])≤1-α

（D）r3:[x]→bn(X)，若 1-α≤p(X|[x])≤α

若P(X|[x])=α时采取肯定决策r1，P(X|[x])=1-α采取否定决策r2，则上述的决策规则变为：

（Y）r1:[x]→pos(X)，若 p(X|[x])≥α

（N）r2:[x]→neg(X)，若 p(X|[x])≤1-α

（D）r3:[x]→bn(X)，若 1-α＜p(X|[x])＜α

于是论域U中的概念X的正域、负域和边界分别为：

pos(X)=∪{[x]|p(X|[x])≥α}

neg(X)=∪{[x]|p(X|[x])≤1-α}

bn(X)=∪{[x]|1-α＜p(X|[x])＜α}

从而概念X的上近似和下近似是：

为一变精度概率粗糙集模型。

（2）若 β=α，显然有 β=α=γ=0.5，此时相应的贝叶斯决策变为：

（Y）r1:[x]→pos(X)，若 p(X|[x])≥0.5

（N）r2:[x]→neg(X)，若 p(X|[x])≤0.5

（D）r3:[x]→bn(X)，若p(X|[x])=0.5

若p(X|[x])=0.5时取决策r3则上述决策变为：

（Y1）r1:[x]→pos(X)，若 p(X|[x])＞0.5

（N1）r2:[x]→neg(X)，若 p(X|[x])＜0.5

（D1）r3:[x]→bn(X)，若 p(X|[x])=0.5

概念X的正域，负域，边界为：

pos(X)=∪{[x]|p(X|[x])＞0.5}

neg(X)=∪{[x]|p(X|[x])＜0.5}

bn(X)=∪{[x]|p(X|[x])=0.5}

X下近似和上近似为：

此时的边界称为概率粗糙集模型(II)的绝对边界为

综上可知，对论域U上的概念X，若X具有最小风险的贝叶斯决策问题，则必存在一个等价的变精度概率粗糙集模型。

4 算例

设U={x1，x2，…，x6}是去医院做诊断的一组病人，特征状态集合为 Ω：{有某种疾病， 无某种疾病}，X：{有病的人}，-X:{无病的人}，决策行为 A={r1，r2，r3}，其中 r1={进行治疗}，r2={不进行治疗}，r3={进一步观察}。风险损失为 :

λ11=0.01，λ31=0.05，λ21=0.15

λ22=0.01，λ32=0.05，λ12=0.15

其中与对象xi有相同属性描述的记为[xi]。

p(X|[x1])=0.23，p(X|[x2])=0.35

p(X|[x3])=0.6，p(X|[x4])=0.74

p(X|[x5])=0.88，p(X|[x6])=0.9

求最小风险的贝叶斯决策。

解：依定理可得：

β=1-0.71=0.29

所以有：

pos(X)={x∈U|p(X|[xi])≥0.71}={x4，x5，x6}

neg(X)={x∈U|p(X|[xi])≤0.29}={x1}

bn(X)={x∈U|0.29≤p(X|[xi])＜0.71}={x2，x3}

因此， 最小风险的贝叶斯决策是：x4，x5，x6需要治疗；x1不需要治疗；x2，x3需要进一步观察。

5 结语

本文针贝叶斯决策过程中的风险损失难以确定的情况，在没有改变贝叶斯决策实质的情况下，加强了对风险损失条件的限定，减小了决策失误的风险；另外，讨论了分析贝叶斯决策过程和变精度概率粗糙集模型的联系，证明了最小风险贝叶斯决策问题可以用一个等价的变精度概率粗糙集模型处理。

[1]张文修,吴伟杰,梁吉业等.粗糙集理论与方法[M].北京：科学出版社,2001.

[2]Pawlak Idzislaw.Rough Set Theory and Its Applications to Data Analysis[J].Cyberaetics and Systems,1998,29(7).

[3]Iarko Wojciech.Variable Precision Rough Set Model[J].J of Computer and System Sciences,1993,46(1).

[4]赵越岭,王建辉.基于变精度粗糙集阈值的选取[J].控制与决策,2007.22(1).

[5]孙秉珍，巩增泰.变精度概率粗糙集模型[J].西北师范大学学报，2005,41(4).

[6]舒宁,马洪超等.模式识别的理论与方法[M].武汉:武汉大学出版社,2004.

[7]张淮中.Bayes决策的概率型粗糙集模型[J].小型微型计算机系统,2004,21(3).